Построение таблиц истинности по функциям

Практическая работа №4

Тема: Построение таблиц истинности по функциям

Цель:

- освоение алгоритма построения таблиц истинности для логических функций;

 - научиться определять и анализировать функции проводимости переключательных схем.

Вид работы: индивидуальный

Время выполнения: 4 часа.

Теоретические сведения

Логическая функция - это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).

Для обозначения новых высказываний наиболее часто используются базовые логические операции, выражаемые словами «И», «ИЛИ», «НЕ».

Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции. При построении таблицы истинности необходимо учитывать порядок выполнения логических операций.

Порядок выполнения логических операций в сложном логическом выражении:

1.     инверсия;

2.     конъюнкция;

3.     дизъюнкция;

4.     импликация;

5.     эквивалентность.

Для изменения указанного порядка выполнения операций используются скобки.

Составленное высказывание, образованное в результате операции логического умножения (конъюнкция), истинно тогда и только тогда, когда истинны входящие в него простые высказывания. Конъюнкция может обозначаться: «И», ^, *, &.

Таблица истинности – это таблица, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции.

Таблица истинности – это таблица, определяющая значение сложного высказывания при всех возможных значениях простых высказываний.

Таблицу, показывающую, какие значения принимает составное высказывание при  всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.

Таблица 3 - Таблицы истинности (при всех возможных значениях логических переменных):

Ход работы

Алгоритм построения таблиц истинности для сложных выражений следующий:

­       Определить количество переменных (простых выражений);

­       Определить количество логических операций и последовательность их выполнения.

­       Определить количество строк:

количество строк = 2^a + строка для заголовка, где a – количество логических переменных.

­       Определить количество столбцов: количество столбцов = количество переменных + количество логических операций;

­       Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.

Пример 1: Построить таблицу истинности для следующего логического выражения

Решение:

­        Простые выражения (логические переменные): А, В, С; (3)

­        Количество логических операций:

­         - инверсия;

­         - операция дизъюнкции;

­         операция конъюнкции. Всего: 3

­        Количество строк: на входе три простых высказывания: А, В, С, поэтому a=3 и количество строк = 2³ +1 = 9.

­        Количество столбцов: 3+3=6

Заполняем столбцы с учетом таблиц истинности логических операций.

Таблица истинности:

Пример 2: Определите истинность составного высказывания состоящего из простых высказываний:

А={Принтер – устройство вывода информации}

В={Процессор – устройство хранения информации}

C={Монитор – устройство вывода информации}

D={Клавиатура – устройство обработки информации}

Установим истинность простых высказываний:

А=1, В=0, С=1, D=0

Определяем истинность составного высказывания:

Пример 3: Доказать равносильность логических выражений:

 и

Таблица истинности

Таблица истинности

Следовательно, =

Пример 3:Запишите логическую функцию, описывающую состояние схемы, составьте таблицу истинности:

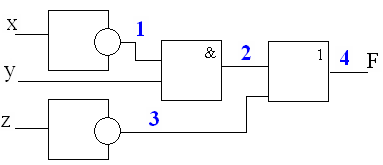
Для записи функции необходимо записать значения на выходе каждого элемента схемы:

1.    

2.    

3.    

4.    

Следовательно, получится функция:

Задания к практической работе

Задание 1. Построить таблицу истинности для логических выражений:

1)    а);                            б) ;

2)    а);                     б) ;

3)    а);                       б) ;

4)    а);                            б) ;

5)    а);                          б) ;

6)    а);                            б) ;

7)    а);                            б) ;

8)    а);              б) .

Задание 2. Запишите логическую функцию, описывающую состояние схемы, составьте таблицу истинности:

Контрольные вопросы и задания

1.           Что такое дизъюнкция? Когда истинна дизъюнкция?

2.           Что такое конъюнкция? Когда истинна конъюнкция?

3.           Как определить количество строк в таблице истинности?

4.           Назвать приоритет логических операций.

5.           Какое количество логических функций двух аргументов существует и почему?

6.           Какие логические функции двух аргументов имеют свои названия?

7.           Какое существует количество логических функций трех аргументов?

8.           Какие законы логики вы знаете?

9.           Какие существуют правила преобразования логических выражений?

Скачано с www.znanio.ru