УДК  372.851

ББК  74.262.21

            В92

Выговская В.В.

В92 Поурочные разработки по математике. 6 класс : пособие для учителя / В.В. Выговская. – 5-е изд., эл. – 1 файл pdf : 496 с. – Москва : ВАКО, 2020. – (В помощь школьному учителю). – Систем. требования: Adobe Reader XI либо Adobe Digital Editions 4.5 ; экран 10″. – Текст : электронный.

ISBN 978-5-408-05332-2

Издание содержит подробные поурочные разработки по математике для 6 класса и ориентировано на учителей, работающих с УМК Н.Я. Виленкина и др. (М.: Мнемозина), но может полноценно использоваться со всеми учебниками для основной школы. Сценарии занятий составлены в соответствии с требованиями ФГОС и содержат все, что необходимо педагогу для качественной подготовки к урокам и их проведения: тематическое планирование учебного материала, методические советы, игровые и логические задачи, контрольные и самостоятельные работы, подробный разбор заданий учебника.

Пособие автономно и содержит материал для проведения уроков в классах различного уровня. Будет полезно как начинающим педагогам, так и преподавателям со стажем.

Подходит к учебникам «Математика» в составе УМК Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шварцбурда 2012–2016 гг. выпуска.

УДК 372.851

ББК 74.262.21

Электронное издание на основе печатного издания: Поурочные разработки по математике. 6 класс : пособие для учителя / В.В. Выговская. – 4-е изд.  – Москва : ВАКО, 2020. – 496 с. – (В помощь школьному учителю). – ISBN 978-5-408-04488-7. – Текст : непосредственный.

В соответствии со ст. 1299 и 1301 ГК РФ при устранении ограничений, установленных техническими средствами защиты авторских прав, правообладатель вправе требовать от нарушителя возмещения убытков или выплаты компенсации.

ISBN 978-5-408-05332-2                                                       © ООО «ВАКО», 2014

От автора

Предлагаемое вам пособие представляет собой переработанное и дополненное в соответствии с требованиями ФГОС издание подробных поурочных планов по математике для 6 класса и ориентировано, прежде всего, на работу с учебно-методическим

комплектом: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 6 класс. Учебник для общеобразовательных учреждений. М.: Мнемозина.

Задача пособия – максимально облегчить учителю как подготовку к уроку, так и работу на уроке. В данной книге учитель найдет подробные конспекты уроков, методические советы, задания на развитие логики и для проверки навыков устного счета, тексты самостоятельных и контрольных работ, задачи повышенной сложности, разбор заданий учебника. Практически все проверочные работы сопровождаются указаниями для учащихся или ответами для эффективной организации работы над ошибками.

Уроки строятся на принципах системно-деятельностного обучения и включают практическую работу, работу в группах и парах, самостоятельную работу с использованием различных форм проверки. То, что ученик не может выполнить индивидуально, он может сделать с помощью соседа по парте или в малой группе. А то, что представляет сложность для конкретной малой группы, становится доступным пониманию в процессе коллективной деятельности.

Планирование предусматривает достижение не только предметных результатов, но и личностных (формирование представлений о математике как о части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества; развитие логического и критического мышления, умения работать в группе, команде; уважение мнения товарищей) и метапредметных (умения анализировать и осмысливать текст задачи, извлекать из текста необходимую информацию, моделировать с помощью схем, рисунков, реальных предметов, строить логическую цепочку, оценивать полученный результат, осуществ4 Примерное тематическое планирование учебного материала лять самоконтроль, доказывать и опровергать утверждения с помощью контрпримеров, классифицировать, исследовать простейшие числовые закономерности).

Все поурочные разработки, содержащиеся в данном пособии, являются примерными. В зависимости от степени подготовленности как целого класса, так и конкретных учащихся учитель может вносить коррективы как в методику проведения урока, так и в саму структуру урока, включая подбор заданий для организации классной, самостоятельной и домашней работы.

Выпускник общеобразовательной школы с целостной системой универсальных знаний, умений и навыков самостоятельной деятельности, гражданской ответственности и правового самосознания, духовности и культуры, инициативный, толерантный, способный к успешной социализации в обществе – таков ориентир в работе учителя.

В целях экономии времени при проверке знаний учащихся предлагаем дополнительно использовать следующие издания:

•    Контрольно-измерительные материалы. Математика. 6 класс / Сост. Л.П. Попова. М.: ВАКО.

•    Сборник практических задач по математике. 6 класс / Сост. В.В. Выговская. М.: ВАКО.

Надеемся, что эта книга оправдает ваши ожидания и действительно поможет в педагогической деятельности.

Примерное тематическое планирование учебного материала

Название темы	Коли- чество часов
ГЛАВА I. ОБЫКНОВЕННЫЕ ДРОБИ
§ 1. Делимость чисел	20
Делители и кратные	3
Признаки делимости на 10, на 5, на 2	3
Признаки делимости на 9 и на 3	2
Простые и составные числа	2
Разложение на простые множители	2
Наибольший общий делитель. Взаимно простые числа	3
Наименьшее общее кратное	4
Контрольная работа № 1 по теме «Делимость чисел»	1

Примерное тематическое планирование учебного материала

Название темы	Коли- чество часов
§ 2. Сложение и вычитание дробей с разными знаменателями	22
Основное свойство дроби	2
Сокращение дробей	3
Приведение дробей к общему знаменателю	3
Сравнение, сложение и вычитание дробей с разными знаменателями	6
Контрольная работа № 2 по теме «Сравнение, сложение и вычитание дробей с разными знаменателями»	1
Сложение и вычитание смешанных чисел	6
Контрольная работа № 3 по теме «Сложение и вычитание смешанных чисел»	1
§ 3. Умножение и деление обыкновенных дробей	32
Умножение дробей	5
Нахождение дроби от числа	4
Применение распределительного свойства умножения	5
Контрольная работа № 4 по теме «Умножение обыкновенных дробей»	1
Взаимно обратные числа	2
Деление	1
Деление	4
Контрольная работа № 5 по теме «Деление обыкновенных дробей»	1
Нахождение числа по его дроби	5
Дробные выражения	3
Контрольная работа № 6 по теме «Дробные выражения»	1
§ 4. Отношения и пропорции	19
Отношения	5
Пропорции	3
Прямая и обратная пропорциональная зависимости	3
Контрольная работа № 7 по теме «Отношения и пропорции»	1
Масштаб	2
Длина окружности и площадь круга	2
Шар	2
Контрольная работа № 8 по теме «Масштаб. Длина окружности и площадь круга»	1

6                                  Примерное тематическое планирование учебного материала

Название темы	Коли- чество часов
ГЛАВА II. РАЦИОНАЛЬНЫЕ ЧИСЛА
§ 5. Положительные и отрицательные числа	13
Координаты на прямой	3
Противоположные числа	2
Модуль числа	2
Сравнение чисел	3
Изменение величин	2
Контрольная работа № 9 по теме «Положительные и отрицательные числа»	1
§ 6. Сложение и вычитание положительных и отрицательных чисел	11
Сложение чисел с помощью координатной прямой	2
Сложение отрицательных чисел	2
Сложение чисел с разными знаками	3
Вычитание	2
Вычитание	1
Контрольная работа № 10 по теме «Сложение и вычитание положительных и отрицательных чисел»	1
§ 7. Умножение и деление положительных и отрицательных чисел	12
Умножение	3
Деление	3
Рациональные числа	2
Свойства действий с рациональными числами	3
Контрольная работа № 11 по теме «Умножение и деление положительных и отрицательных чисел»	1
§ 8. Решение уравнений	15
Раскрытие скобок	4
Коэффициент	2
Подобные слагаемые	3
Контрольная работа № 12 по теме «Подобные слагаемые»	1
Решение уравнений	4
Контрольная работа № 13 по теме «Решение уравнений»	1
§ 9. Координаты на плоскости	13
Перпендикулярные прямые	2
Параллельные прямые	2

Примерное тематическое планирование учебного материала

Название темы	Коли- чество часов
Координатная плоскость	3
Столбчатые диаграммы	2
Графики	3
Контрольная работа № 14 по теме «Координаты на плоскости»	1
ПОВТОРЕНИЕ	18
Признаки делимости на 10, на 5, на 2, на 3, на 9	1
Сравнение, сложение и вычитание дробей с разными знаменателями	1
Сложение и вычитание смешанных чисел	1
Умножение и деление дробей	1
Нахождение дроби от числа и числа по его дроби	1
Отношения. Пропорции. Масштаб	1
Сложение и вычитание положительных и отрицательных чисел	1
Умножение и деление положительных и отрицательных чисел	1
Свойства действий с рациональными числами	1
Подобные слагаемые	1
Решение уравнений	1
Контрольная работа № 15 по теме «Повторение»	1
Повторение по результатам анализа контрольной работы	6
Итого	175

Глава I 

ОБЫКНОВЕННЫЕ ДРОБИ

§ 1. ДЕЛИМОСТЬ ЧИСЕЛ

Планируемые результаты

•    Завершить изучение натуральных чисел.

•    Подготовить основу для освоения действий с обыкновен-ными дробями.

•    Формулировать определения делителя и кратного, которые находят применение при сокращении обыкновенных дробей и при их приведении к общему знаменателю.

•    Формулировать понятия простого и составного чисел.

•    Формулировать свойства и признаками делимости.

•    Решать задачи, связанные с делимостью чисел.

•    Уметь проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило.

•    Доказывать и опровергать с помощью контрпримеров утверждения о делимости чисел.

•    Классифицировать натуральные числа (четные и нечетные, по остаткам от деления на 3 и т. п.).

Информация для учителя.  Учащиеся должны уметь разло-

жить число на множители. Например, они должны понимать, что 36 = 6 · 6 = 4 · 9.

Последовательно кратные данного числа можно найти, умножая его на 1, 2, 3 и т. д. или прибавляя данное число к предыдущему кратному.

У р о к 1. Делители и кратные

Цели: ввести понятия делителя и кратного натурального числа; отрабатывать умение находить делители и кратные данного натурального числа; совершенствовать устные и письменные вычислительные навыки; развивать математическую речь учащихся.

Урок 1. Делители и кратные

Х о д у р о к а

I.  Организационный момент. Мотивация к учебной деятельности (Учитель приветствует учащихся, проверяет готовность к уроку.)  – Придумайте девиз нашего урока.

II.  Практическая деятельность учащихся

–    Найдите значение выражений: 100 : 25; 66 : 4; 66 : 1; 66 : 11; 100 : 1; 100 : 24; 72 : 1; 72 : 3; 72 : 72; 66 : 66; 72 : 8; 100 : 100.

–    На какие группы можно разделить данные числовые выраже-ния? Почему? (Ответ. На две группы: 1-я группа – деление без остатка, 2-я группа – деление с остатком; на три группы (по делимому): 1-я группа – делимое = 100, 2-я группа – делимое = 66, 3-я группа – делимое = 72; на три группы (по делителю): 1-я группа – делитель = 1, 2-я группа – делитель = самому числу, 3-я группа – делитель = другим числам.)

–    Когда одно число делится на другое без остатка, то говорят, что первое число делится на второе. На доске: а : b = c

–    Как называются числа при делении? (Ответ. а – делимое, b – делитель, c – частное.)

–    Какое число получится при делении числа 100 на число 4?

–    Делимое 1000, делитель 4. Найдите частное.

–    Делитель 8, частное 25. Найдите делимое.

–    Делимое 1000, частное 125. Найдите делитель.

На доске: x : 2 = 19; 42 : x = 14

–    Как называются данные равенства? (Уравнения.)

–    Как найти неизвестное делимое? (Чтобы найти неизвестное

делимое, надо частное умножить на делитель.)

–    Как найти неизвестный делитель? (Чтобы найти неизвест-

ный делитель, надо делимое разделить на частное.)

–    Назовите корень уравнения x, если x + 1 = 10. (9.)

–    Назовите наименьшее натуральное число. (1.)

–    Какие числа называют натуральными? (Числа, которые используются при счете предметов.)

–    Назовите наибольшее натуральное число. (Такое число назвать невозможно, так как натуральных чисел бесконечно много.) III.  Сообщение темы урока

–    С какими новыми понятиями мы сегодня познакомимся на уроке?

(Ученики самостоятельно формулируют тему урока. Учитель записывает ее на доске, дети – в тетрадях. Заранее приготовлено оформление доски, способствующее более интересному и наглядному проведению урока.)

IV.  Подготовка к работе на основном этапе 1. Прочитайте задачу на с. 4 в начале § 1.

Задача. 20 яблок надо разделить поровну между 4 ребятами. Сколько яблок получит каждый ребенок? (Каждый получит по 5 яблок.)

–    А если надо разделить (не разрезая) 20 яблок между 6 ребя-тами? Сколько яблок получит каждый ребенок? (Каждый

получит по 3 яблока, а еще 2 яблока останутся.)

–    Говорят, что число 4 является делителем числа 20, а число 6 не является делителем числа 20.

Определение. Делителем натурального числа a называют нату-

ральное число b, на которое а делится без остатка.

–    Запишем в тетрадь: a : b; число b – делитель числа а; а, b – натуральные числа.

–    Назовите делители числа 12. (1, 2, 3, 4, 6 и 12.)

2. С. 4, № 1 (устно).

Ответ: по 1 ореху – 36 кучек, по 2 – 18 кучек, по 3 – 12 кучек,

по 4 – 9 кучек, по 6 – 6 кучек.

–    Что можно сказать об этих числах? (Они являются делите-

лями числа 36.)

3. С. 4, № 2 (устно).

–    Ответьте на 1-й вопрос. (Да.)

–    Почему? (42 делится на 6 без остатка.)

–    Ответьте на 2-й вопрос. (Нет.)

–    Почему? (Так как 49 не делится на 6 без остатка.)

4. Прочитайте задачу на с. 4.

Задача. Пусть на столе лежат пачки, в каждой из которых по 8 печений. Можно ли, не раскрывая пачек, взять 8 печений? (Да.) 16 печений? (Да.) 24 печенья? (Да.) А 18 печений? (Нет, не раскрывая пачек, взять18 печений нельзя.)

–    Говорят, что числа 8, 16, 24 кратны числу 8, а число 18 не кратно числу 8.

Определение. Кратным натурального числа а называют нату-

ральное число с, которое делится без остатка на а.

–    Запишем в тетрадь: с : а, число с – кратное числа а; с, а – натуральные числа.

«“Крата” – старинное русское слово, означающее “раз”. Слово “кратный” означает “известное число раз”. Сколь кратно говорено тебе! Однократный, многократный проступок» (из «Толкового словаря живого великорусского языка» В.И. Даля).

5. Назовите числа, кратные числу 10. (10, 20, 30, 40, …)

–    Можно ли назвать самое большое число, кратное числу 10?

(Нет.)

Урок 1. Делители и кратные

–    Почему? (Натуральных чисел бесконечно много.)

–    Какой вывод можно сделать? (Любое натуральное число имеет бесконечно много кратных.)

V.  Усвоение новых знаний и способов действий

 – Давайте договоримся, что на всех уроках в случае затруднений вы будете обращаться за помощью к учителю или к ученикам-консультантам. Для получения консультации достаточно поднять красную сигнальную карточку со знаком вопроса.

1.                    Прочитайте текст в учебнике на с. 5 в рубрике «Говори правильно».

2.                    С. 4, № 3 (а, д) (устно, ответ обоснуйте).

Ответ: а) да, верно, 5 – делитель 45, так как 45 : 5 = 9, т. е. 45 делится на 5 без остатка; д) неверно, так как 6 не делится на 12 без остатка.

3.                    С. 5, № 5 (а, б) (устно).

Ответ: а) 4, 10 (20 делится на 4, 20 делится на 10); б) 4, 8, 12, 16 (4 кратно 4, так как 4 делится на 4; 8 кратно 4, так как 8 делится на 4, и т. д.).

VI.  Самостоятельная работа и осуществление контроляВариант 1. С. 5, № 6 (а), 7 (б); с. 7, № 20 (в, е).

Вариант 2. С. 5, № 6 (б), 7 (в); с. 7, № 20 (г, д).

(Учащиеся, которые справятся с заданием раньше других, могут наряду с учителем выступать в роли консультантов (в том случае, если не выставляется оценка).)

VII.               Рефлексия учебной деятельности и оценивание учащихся             – С какими новыми понятиями мы познакомились на уроке?

                   – Назовите делители числа 8 и три числа, кратные числу 8.

Домашнее задание

С. 8, № 25 (1); с. 9, № 27 (а, в), 30 (а, б).

(В зависимости от уровня класса домашнее задание может быть уменьшено или увеличено по усмотрению учителя, но оно не должно превышать треть заданий, выполненных на уроке. По времени должно занимать не больше 20 мин, некоторые номера можно предлагать только более подготовленным учащимся (индивидуальные домашние задания), но другие ученики могут их сделать, если у них есть желание.

Можно предложить ученикам зафиксировать, сколько времени они тратят на выполнение домашнего задания по математике, продумать систему поощрений за дополнительно выполненные номера.)

У р о к 2. Делители и кратные

Цели: отрабатывать умения учащихся находить делители и кратные чисел; учить рассуждать и логически мыслить; воспитывать умение оценивать труд товарищей.

Х о д у р о к а

I.  Организационный момент. Мотивация к учебной деятельности Девизом нашего урока будут слова Антона Павловича Чехова: «Нужно стремиться к тому, чтобы каждый видел и знал больше, чем видел и знал его отец и дед».

II.  Сообщение целей и задач урока

 – Как вы думаете, чем мы будем сегодня заниматься на уроке? (Находить делители и кратные чисел, а также решать комбинаторные задачи.)

III.  Практическая деятельность учащихся

(Повторение правил действий с десятичными дробями.)

1.       С. 6, № 15 (устно), в тетрадь записать только ответы (фронтальная проверка).

2.       Какие из чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 являются делителями чисел 18, 30, 36, 42?

3.       В классе 24 ученика. Их надо разделить на одинаковые группы. По сколько человек может быть в этих группах?

              – Что нужно сделать, чтобы ответить на вопрос задачи? (Най-

ти делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24.)

4. Что означает латинское слово «centum»? (Сто.)

 – Какое слово произошло от этого латинского слова? (Процент.) IV.  Индивидуальная работа. Осуществление коррекции знаний

(Во время проведения устного счета несколько учеников работают по индивидуальным карточкам. Можно эти карточки выдавать и на других этапах урока учащимся, которые работают быстрее других.)

№ п/п	Выразите  десятичной дробью	Выразите  в процентах	Найдите
1	56%	0,33	2% от 100
2	160%	0,4	24% от 200
3	25%	0,05	400% от 3
4	6%	0,107	6% от 40
5	2,1%	52	80% от 500
6	234%	1,73	45% от 500
7	80%	0,006	15% от 700

Урок 2. Делители и кратные

V.  Подготовка к работе на основном этапе

–    Какое натуральное число называют делителем данного на-турального числа?

–    Запишите в порядке возрастания все делители чисел 6, 20, 32, 17.

–    Какую закономерность вы заметили? (Число 1 является де-

лителем всех этих чисел, и все числа делятся на самих себя.)

–    Правильно, число 1 является делителем любого натураль-ного числа. Также оно является делителем для самого себя.

–    Какое натуральное число называют кратным данному на-туральному числу? (Само это число.)

–    Запишите в тетрадь 3 числа, кратных числам 15, 23 и 41.

–    Какими способами находили кратные? (Последовательно кратные данного числа можно получать, умножая его на 1, 2, 3 и т. д. или прибавляя данное число к предыдущему кратному.)

–    Назовите наименьшее число из кратных числу 15. (15.)

–    Назовите наименьшее число из кратных числу 23. (23.)

–    Назовите наименьшее число из кратных числу 41. (41.)

–    Какой вывод можно сделать? (Наименьшим из кратных натурального числа является само это число.)

Сейчас я вам покажу, как можно находить сразу два делителя числа 84.

Делитель	1	2	3	4	6	7
Частное	84	42	28	21	14	12

Делители 1 и 84, 2 и 42, 3 и 28, 4 и 21, 6 и 14, 7 и 12 называют парными делителями.

–    Сформулируйте определение парных делителей. (Произве-

дение парных делителей равно самому числу.)

–    Приведите примеры парных делителей. (Ответы учеников.) – Запишите в порядке возрастания все делители числа 84.

Сколько их? (Делители числа 84: 1, 2, 3, 4, 6, 7, 12, 14, 21,

28, 42, 84.)

–    Запишите в порядке возрастания все делители числа 96.

Делитель	1	2	3	4	6	8
Частное	96	48	32	24	16	12

(1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96.) VI.  Работа над задачей

1. С. 7–8, № 23.

–    Прочитайте задачу.

–    Как вы понимаете задачу?

–    Давайте вместе разберем решение задачи по учебнику.

Задачи, для решения которых рассматриваются все возможные комбинации, называют комбинаторными. Комбинаторика – это раздел математики, занимающийся комбинаторными задачами.

2. С. 8, № 24.

–    Прочитайте задачу.

–    Как вы понимаете задачу?

–    Какого цвета у нас будет верхняя полоса? (Белого.)

–    Какого цвета может быть средняя полоса? (      Зеленого, красного или синего.)

–    Если средняя полоса зеленая, какого цвета будет нижняя?  (Красного или синего.) И т. д.

–    Рассмотрим составление всевозможных вариантов флага с помощью графа, называемого деревом (за внешнее сходство с деревом).

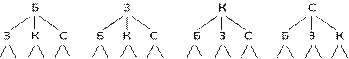
          К С З С З К             К С Б С Б К               З С Б С Б З             З К Б К Б З

Можно пользоваться следующим правилом, которое получило в комбинаторике название «правило произведения».

Если существует n вариантов выбора первого элемента и для каждого из них есть m вариантов выбора второго элемента, то всего существует n · m различных пар с выбранными первым и вторым элементами.

Это правило справедливо для любого количества элементов.

Всего по правилу произведения получили 4 · 3 · 2 = 24 (комбинации) – 24 варианта флага.

Государственный флаг Российской Федерации трехцветный:

белый, синий, красный.

VII.  Усвоение новых знаний и способов действий

1.  С. 6, № 8 (ответ обоснуйте).

2.  С 6, № 9.

                   – Как доказать, что число 70 525 кратно числу 217? (Нужно

70 525 разделить на 217, если оно делится нацело, то является кратным.)

Решение: 70 525 : 217 = 325, следовательно, число 70 525 кратно

числу 217.

3. Найдите несколько общих кратных чисел:

а) 4 и 5; б) 8 и 12; в) 6 и 9; г) 10 и 15.

Ответ: а) 20, 40; б) 24, 48; в) 18, 36; г) 30, 60.

Урок 3. Делители и кратные

VIII. Самостоятельная работа и осуществление контроляВариант 1. С. 5, № 6 (в); с. 7, № 19 (б), 20 (а).

Вариант 2. С. 5, № 6 (г); с. 7, № 19 (а), 20 (б).

–    У кого возникли вопросы?

IX.     Рефлексия учебной деятельности и оценивание учащихся – Мы претворили в жизнь девиз урока?

–    Какое натуральное число является делителем любого нату-рального числа?

–    Как называются задачи, которые мы решали на уроке?

–    Как называется раздел математики, изучающий комбина-торные задачи?

Домашнее задание

С. 8, № 25 (2), 26; с. 9, № 30 (в).

У р о к 3. Делители и кратные

Цели: закрепить умение находить делители и кратные чисел; развивать грамотную математическую речь; проверить знания и умения учащихся по изученному материалу.

Информация для учителя.  Создать в классе уголок «Истори-

ческая справка».

Х о д у р о к а

I.  Организационный момент. Мотивация к учебной деятельности II.  Сообщение темы урока

 – Разгадав анаграмму, вы прочитаете тему нашего урока. ЕИЕИЛТЛД и КРТНЕЫА (Делители и кратные.) III.  Практическая деятельность учащихся

1. С. 7, № 22 (устно).

 – Кто не согласен с моими ответами? (Если у учащихся есть ошибки, то вспомнить правила действий с десятичными дробями.)

А вы знаете, кто первым описал вычисления с десятичными дробями? Ученый Средневековья аль-Каши Джемшид Ибн Масуд. В России в 1703 г. Петр I организовал издание первого учебника по математике. Так появилась «Арифметика» Леонтия Филипповича Магницкого – учение о десятичных дробях.

2.  Назовите:

а) три числа, для которых 18 будет кратным;

б) три числа, которые будут кратными числа 18;

в) все числа, для которых число 12 будет кратным.

3.  Спутник Земли делает один оборот за 1 ч 40 мин, а второй оборот – за 100 мин. Как такое может быть? (1 ч 40 мин = 100 мин.)

IV.  Индивидуальная работа. Осуществление коррекции знаний Карточка 1

1.  Неизвестное слагаемое равно:

а)  слагаемое − сумма;

б)  сумма − слагаемое;

в)  сумма + слагаемое.

2.  Неизвестное уменьшаемое равно:

а)  разность − вычитаемое;

б)  вычитаемое − разность;

в)  вычитаемое + разность.

3.  Неизвестный делитель равен:

а)  делимое : частное;

б)  частное · делимое;

в)  частное : делимое. Карточка 2

1.  Неизвестный множитель равен:

а)  произведение : множитель;

б)  произведение − множитель;

в)  множитель : произведение.

2.  Неизвестное вычитаемое равно:

а)  уменьшаемое + разность;

б)  уменьшаемое − разность;

в)  разность − уменьшаемое.

3.  Неизвестное делимое равно:

а)  делитель · частное;

б)  делитель : частное;

в)  частное : делитель.

V.  Усвоение новых знаний и способов действий 1. С. 5, № 4.

Ответ: а) да, 15 – делитель 105, так как 105 делится на 15 без остатка, 105 : 15 = 7; б) да, частное 105 : 15 является делителем числа 105, так как при делении 105 на 15 получается 7.

2.  С. 5, № 7 (а, г).

3.  (Повторить понятие координатного луча. Работа у доски и в тетрадях с подробным комментированием.)

а) С. 6, № 10.

б) С. 7, № 17.

VI.  Работа над задачей

1.  У продавца много гирь массой 3 кг и 5 кг. Может ли он взвесить товар массой 29 кг? (Может.)

Урок 4. Признаки делимости на 10, на 5, на 2

2.  Можно ли 64 ручки разложить поровну:

        а) в 10 наборов;                          в) в 16 наборов;

б) в 32 набора;   г) в 22 набора?  – Ответ обоснуйте.

VII.  Самостоятельная работа и осуществление контроля Вариант 1

1.  Запишите в порядке возрастания все делители числа 36.

2.  Запишите кратные числа 14, но меньшие 50.

3.  Запишите 3 числа, кратные числу n.

4.  Назовите три натуральных числа, для которых число 24:

а) будет кратным;      б) будет делителем. Вариант 2

1.  Запишите в порядке убывания все делители числа 24.

2.  Запишите числа, кратные 25, но меньшие 101.

3.  Запишите 3 числа, кратные числу t.

4.  Назовите три натуральных числа, для которых число 36:

        а) будет кратным;                      б) будет делителем.

VIII.  Рефлексия учебной деятельности и оценивание учащихся

–    Какое число и кратно числу n, и является делителем числа n?

–    Какое число является кратным любому натуральному чис-лу? (Число 0 кратно любому натуральному числу, так как

0 делится без остатка на любое натуральное число.)

Домашнее задание

С. 9, № 27 (в, г), 28, 30 (г).

У р о к 4. Признаки делимости  на 10, на 5, на 2

Цели: познакомить учащихся с признаками делимости на 10, на 5, на 2; ввести определение четных и нечетных чисел; повторить порядок действий; учить рассуждать и логически мыслить.

Х о д у р о к а

I.  Организационный момент. Мотивация к учебной деятельности II.  Актуализация знаний

1.       Познакомить учащихся с результатами самостоятельной работы.

2.       Выполнить задания, в которых допущено наибольшее количество ошибок.

III.  Практическая деятельность учащихся

1. 347 : 10; 3000 : 10; 464 : 2; 155 : 5; 125 : 5; 441 : 2; 670 : 1; 284 : 2; 648 : 2; 575 : 5; 101: 5; 340 : 10.

 – На какие группы можно разделить данные числовые выражения? Почему? (Ответ. На три группы – деление чисел на 2, на 5, на 10; на две группы – числа, которые делятся нацело, и числа, при делении которых получается остаток; на четыре группы – числа, которые делятся на 2, на 5, на 10 без остатка, и числа, при делении которых на 2, на 5, на 10

получается остаток.)

2. Периметр квадрата равен 36 см. Найдите площадь квадрата.

(36 : 4 · 9 = 81 см².)

3. Чему равно произведение всех цифр? (0.)

IV.  Индивидуальная работа. Осуществление коррекции знаний

        Карточка 1                                           Карточка 2

       8х + 2х + 3х = 130;                              17х − 7х + 40 = 170;

15х − 5х + 20 = 180; 6х + 5х + 4х = 150; 60 − (х + 7) = 34;          (х − 8) + 30 = 65;

450 − 3х = 150;          310 + 7х = 380; 50 : х + 48 = 50.   90 : х − 32 = 13.

V.  Сообщение темы урока

Сегодня на уроке мы научимся определять, делится ли одно число на другое, не выполняя деление. Существуют признаки, помогающие по записи числа определить, делится ли оно на какое-то число.

VI.  Подготовка к работе на основном этапе

–    При умножении натурального числа на 10 получается чис-ло, оканчивающееся нулем. Поэтому всякое натуральное число, оканчивающееся цифрой 0, делится без остатка на 10. Чтобы получить частное, достаточно отбросить эту цифру 0.

–    Найдите значение выражения:

23 400 : 10; 547 890 : 10; 62 370 : 10; 568 300 : 10.

–    Эти числа делятся без остатка на 10.

–    Проверьте, делятся ли эти числа (283 и 548) на 10.

(При делении числа 283 на 10 получаем неполное частное 28 и остаток 3; при делении числа 548 на 10 получаем неполное частное 54 и остаток 8.)

–    Сравните остатки от деления с последней цифрой чисел.

–    Что интересного заметили? (Остаток от деления равен цифре записи этого числа.)

Урок 4. Признаки делимости на 10, на 5, на 2

–    Какой вывод можно сделать? (Если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.)

–    Сформулируйте признак делимости чисел на 10.

–    Прочитайте, как сформулирован этот признак на с. 9.

–    Назовите 3 числа, которые делятся на 10, и 3 числа, которые на 10 не делятся.

–    Прочитайте самостоятельно на с. 9 текст после признака делимости на 10.

–    Почему любое число, запись которого оканчивается ци-фрой 0, делится без остатка и на 2, и на 5?

–    Приведите примеры, подтверждающие это.

–    Как в учебнике доказывается признак делимости числа на 5?

–    Приведите примеры чисел, делящиеся на 5, и чисел, не де-лящихся на 5.

Определение. Числа, делящиеся без остатка на 2, называются

четными, а числа, которые при делении на 2 дают остаток 1, называются нечетными.

Цифры 0, 2, 4, 6, 8 называют четными, а цифры 1, 3, 5, 7, 9 –

нечетными.

–    Сформулируйте самостоятельно признак делимости на 2.

–    Приведите примеры трехзначных четных чисел, двузначных нечетных чисел.

(Можно записать в тетрадь памятку для учащихся.)

1.  Число, оканчивающееся на четную цифру, делится на 2.

2.  Число, оканчивающееся на 0 или 5, делится на 5.

3. Число, оканчивающееся на 0, делится на 10. VII.  Усвоение новых знаний и способов действий

1.  С. 10, № 31.

(Красным карандашом подчеркнуты четные числа, т. е. числа, которые без остатка делятся на 2; синим – числа, которые делятся без остатка на 5; красным и синим цветом – числа, которые делятся без остатка на 10; 1, 3, 7, 9, 11, 13, 17, 19, 21, 23, 27, 29.)

2.  Сколько различных трехзначных чисел можно записать с помощью цифр 0, 6, 9? Цифры могут повторяться.

–    К какому виду относится данная задача? ( Это комбинаторная задача.)

–    Какие цифры могут быть на месте сотен, десятков и еди- ниц? (На месте сотен могут быть только цифры 6 или 9, на месте десятков и единиц – все три цифры.)

Определение. Графы – геометрические фигуры, состоящие из точек (их называют вершинами) и соединяющих их отрезков (называемых ребрами графа).

(Эту схему составляет учитель на доске.)

Решение. Подсчет вариантов выполним с помощью графа, называемого деревом.

Ребра графа, являющегося деревом, иногда называют ветвями дерева, а само дерево – деревом вариантов. Дерево вариантов дает наглядное представление о том, как применяется правило произведения для подсчета комбинаций из большего, чем 2, числа элементов.

                                 6                                                           6

                                 9                                                           9

        6            0   6     9     0   6            0        6            0   6     9     0   6            0

Или по правилу произведения получаем: 2 · 3 · 3 = 18 (чисел). Ответ: 18 чисел.

3. С. 11, № 35 (а).

           – Определите, сколько чисел мы должны записать.

Решение. Первой цифрой числа может любая из двух цифр (2 или 5, так как число не может начинаться с нуля), второй – любая из трех (0, 2, 5), а третьей – любая из двух (0, 2, так как должно выполняться условие: число делится на 2): 2 · 3 · 2 = 12 (чисел). Ответ: 222; 220; 252; 250; 202; 200; 522; 520; 552; 550; 502; 500.

4. С. 11, № 36 (ответ обоснуйте).

Ответ: 32 яйца Коля принести не может, так как число 32 не делится на 10 без остатка.

VIII.  Самостоятельная работа и осуществление контроля Вариант 1. С. 10, № 32 (а, в), 33 (а, г).

Вариант 2. С. 10, № 32 (б, г), 33 (б, в).

IX.  Включение в систему знаний и повторение

–    Какие действия относятся к действиям первой ступени и ка-кие – к действиям второй ступени? (Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.)  – Вспомните правила выполнения действий.

–    Можно ли изменять порядок действий? (Изменять поря-

док действий можно на основе свойств сложения, вычитания и умножения.)

–    Назовите первое действие и т. д. (Порядок действий обо-значьте цифрами и обведите в кружок.)

 5 1 8 6 2 9 3 7 10 4

a · b² + c · d³ − e² : f + k³

Урок 5. Признаки делимости на 10, на 5, на 2

Решение:

1) b · b; 2) d · d · d; 3) e · e; 4) k · k · k; 5) a · 1; 6) c · 2; 7) 3 : f; 8) 5 + 6; 9) 8 − 7; 10) 9 + 4.

1. Самостоятельно запишите порядок действий: a · (b² + c) · d³ − e² : (f + k³).

            – У кого получился другой порядок действий?

2. С. 13, № 54.

–    Решим задачу алгебраическим способом. Что это значит?

(С помощью уравнения.)

–    Что значит, число увеличили в 11 раз? (Умножили на 11.)

–    Что значит, результат уменьшили на 2,75? (Вычли из полученного результата 2,75.) Решение:

(Все подсчеты выполняются в тетради.)

1-й способ (алгебраический)

Пусть х – задуманное число.

х · 11 − 2,75 = 85,25 х · 11 = 85,25 + 2,75 х = 8 Ответ: 8.

2-й способ (арифметический)

1)  85,25 + 2,75 = 88

2)  88 : 11= 8

Ответ: 8.

X.  Рефлексия учебной деятельности и оценивание учащихся  – Что нового и интересного узнали на уроке?

–    Какие цифры называют четными?

–    Приведите примеры четных чисел.

–    Какие цифры называют нечетными?

–    Приведите примеры нечетных чисел.

Домашнее задание

С. 11, № 39 (по желанию учащихся); с. 13, № 54 (2), 55, 60 (а, б).

У р о к 5. Признаки делимости  на 10, на 5, на 2

Цели: научить использовать признаки делимости при выполнении упражнений и решении задач; совершенствовать устные и письменные вычислительные навыки; развивать умение решать уравнения, логическое мышление.

Х о д у р о к а

I.    Организационный момент. Мотивация к учебной деятельности

II.  Устная контрольная работа

Вариант 1

1)  2,5 · 2,7 · 0,04;

2)  1,25 · 1,9 · 0,8;3) 0,5 · 20 : 0,1;

4)   5,4 · 1,7 − 2,4 · 1,7;

5)   1 − 0,32;

6)   0,6 + 0,02 − 0,2;

7)   9,1 · 3,7 + 9,1 · 6,3; 8) 3 : 4; 9) (0,7 − 0,06) : 8; 10) 2³ · 3².

III.  Сообщение темы урока Вариант 2

1)  12,5 · 3,2 · 0,8;

2)  0,25 · 5,1 · 0,04;3) 0,6 · 40 : 0,1;

4)           5,3 · 7,2 − 5,3 · 3,2;

5)           1 − 0,67;

6)           0,8 + 0,04 − 0,4;

7)           4,9 · 2,4 + 4,9 · 7,6; 8) 2 : 5; 9) (0,9 − 0,09) : 9; 10) 33 · 22.

–    Как вы думаете, чем мы будем заниматься сегодня?IV.  Подготовка к работе на основном этапе

1. С. 10, № 34.

–    Сформулируйте признак делимости на 100, 1000 и т. д.

2. С. 11, № 38 (а).

Слагаемое	Слагаемое	Сумма
a	b	a + b
четное	нечетное	нечетное
четное	четное	четное
нечетное	четное	нечетное
нечетное	нечетное	четное

–    Приведите примеры, доказывающие ваши ответы.

3. С. 12, № 45.

а) Если каждое слагаемое кратно числу а, то и сумма кратна

числу а.

32 : 8, 56 : 8, 88 : 8, следовательно, (32 + 56 + 88) : 8.

–    Проверьте истинность этого высказывания с помощью вы-числений.

(32 + 56 + 88) : 8 = 176 : 8 = 22.

б) Если только одно слагаемое суммы не кратно числу а,

то и сумма не кратна числу а.

15 : 5, 35 : 5, 18 не делится на 5, следовательно, (15 + 35 + 18) не делится на 5.

(15 + 35 + 18) : 5 = 68 : 5 = 13 (остаток 3).

Урок 5. Признаки делимости на 10, на 5, на 2

V.  Усвоение новых знаний и способов действий

1.  С. 11, № 37 (ответ обоснуйте).

Ответ: 92 карандаша не может оказаться, так как 92 не делится на 5 без остатка.

2.  С. 11, № 35 (б).

Ответ: 225; 220; 255; 250; 205; 200; 525; 520; 555; 550; 505; 500.

3.  С. 12, № 47 (работа в паре).

Решение:

а) делители 100: 10, 20, 25, 50;

б) кратные 25: 25, 50, 75;

в) делители 100 и кратные 25: 25, 50.

VI.  Самостоятельная работа и осуществление контроля Вариант 1. С. 10, № 39 (а, г), 40 (а, г).

Вариант 2. С. 11, № 39 (б, в), 40 (б, в).

VII.  Включение в систему знаний и повторение

1. С. 12, № 50.

–    Какие дроби называются правильными?

–    Какие дроби – неправильными?

2. С. 12, № 51.

Ответ: а = 4, 5, 6, 7, 8, 9, 10.

             – Как по-другому можно записать ответ? (В виде двойного не-

равенства 4 ≤ а ≤ 10, где а – натуральное число.)

Ответ: b = 1, 2, 3, 4, 5, 6, 7; 1 ≤ b ≤ 7, где b – натуральное число.

3. С. 12, № 52 (а, б).

1-й способ

а) (х + 2,3) · 0,2 = 0,7 х + 2,3 = 0,7 : 0,2 х = 1,2

–    Как выполняется деление десятичной дроби на десятичную дробь?

–    Давайте решим это уравнение другим способом, применив распределительное свойство умножения.

2-й способ

а) (х + 2,3) · 0,2 = 0,7 0,2х + 2,3 · 0,2 = 0,7 х = 1,2

–    Что нужно помнить об умножении десятичной дроби на де-сятичную дробь?

Ответ: а) 1,2; б) 1,3.

VIII.  Рефлексия учебной деятельности и оценивание учащихся  – Что нового узнали на уроке, что повторили?

–    Что вам понравилось на уроке?

–    С какими трудностями столкнулись на уроке?

Домашнее задание

С. 13, № 56, 59 (а), 60 (в).

У р о к 6. Признаки делимости  на 10, на 5, на 2

Цели: формировать умения и навыки использования признаков делимости; развивать умение решать комбинаторные задачи; проверить знания и навыки учащихся по изученному материалу.

Х о д у р о к а

I.  Организационный момент. Мотивация к учебной деятельности II.  Практическая деятельность учащихся

1. 267 000 : 1000; 34 600 : 100; 34 000 : 1000; 34 500 : 100; 230 000 : 1000; 23 000 : 100.

           – Сформулируйте признак делимости на 100, 1000 и т. д.

2. Решите уравнение: y : 3 = 15; y − 3 = 15; y + 3 = 15; y · 3 = 15.

           – Что интересного заметили? В чем сходство? В чем различие?

3. Какие дроби называются правильными? Какие – неправильными?

                – Назовите 3 правильные дроби со знаменателем 8.           – Назовите 3 неправильные дроби с числителем 12.

4. Задача. В шахматном турнире участвуют 6 человек. Каждый друг с другом должен сыграть партию. Сколько партий будет сыг-

рано? (6 · 5 : 2 = 15.)

III.  Индивидуальная работа. Осуществление коррекции знаний

Карточка 1. I уровень

Решите уравнение относительно x:

1) a + x = c;  3) a : x = c; 2) x − b = c;    4) x · b = c.

Карточка 2. II уровень

Решите уравнение относительно x:

1) (a + b) · x = c;          3) x · (a − b) = c; 2) (a − b) : x = c; 4) x : (a + b) = c.

Карточка 3. Повышенный уровень Решите уравнение относительно x:

1)  (a + b) · (x − d) = c;               3) dx · (a − b) = c;

2)  (a − b) : (x + d) = c;               4) dx : (a + b) = c.

Содержание

От автора  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Примерное тематическое планирование учебного материала  . . . . . . . . 4

ГЛАВА I. ОБЫКНОВЕННЫЕ ДРОБИ

§ 1. Делимость чисел

У р о к 1. Делители и кратные  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 У р о к 2. Делители и кратные  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

У р о к 3. Делители и кратные  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 У р о к 4. Признаки делимости на 10, на 5, на 2  . . . . . . . . . . . . . . . . . . . 17

У р о к 5. Признаки делимости на 10, на 5, на 2  . . . . . . . . . . . . . . . . . . . 21

У р о к 6. Признаки делимости на 10, на 5, на 2  . . . . . . . . . . . . . . . . . . . 24

У р о к 7. Признаки делимости на 9 и на 3  . . . . . . . . . . . . . . . . . . . . . . . 27

У р о к 8. Признаки делимости на 9 и на 3  . . . . . . . . . . . . . . . . . . . . . . . 31 У р о к 9. Простые и составные числа  . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 У р о к 1 0. Простые и составные числа  . . . . . . . . . . . . . . . . . . . . . . . . . . 38 У р о к 1 1. Разложение на простые множители  . . . . . . . . . . . . . . . . . . . 41

У р о к 1 2. Разложение на простые множители  . . . . . . . . . . . . . . . . . . . 45 У р о к 1 3. Наибольший общий делитель  . . . . . . . . . . . . . . . . . . . . . . . . 48 У р о к 1 4. Наибольший общий делитель. Взаимно простые числа  . . . 53

У р о к 1 5. Наибольший общий делитель. Взаимно простые числа  . . . 57

У р о к 1 6. Наименьшее общее кратное  . . . . . . . . . . . . . . . . . . . . . . . . . 60

У р о к 1 7. Наименьшее общее кратное  . . . . . . . . . . . . . . . . . . . . . . . . . 65

У р о к 1 8. Наименьшее общее кратное  . . . . . . . . . . . . . . . . . . . . . . . . . 67

У р о к 1 9. Наименьшее общее кратное  . . . . . . . . . . . . . . . . . . . . . . . . . 70

У р о к 2 0. Контрольная работа № 1  . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

§ 2. Сложение и вычитание дробей с разными знаменателями

У р о к 2 1. Основное свойство дроби  . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74 У р о к 2 2. Основное свойство дроби  . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 У р о к 2 3. Сокращение дробей  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82

У р о к 2 4. Сокращение дробей  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87

У р о к 2 5. Сокращение дробей  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89 У р о к 2 6. Приведение дробей к общему знаменателю  . . . . . . . . . . . . 92

У р о к 2 7. Приведение дробей к общему знаменателю  . . . . . . . . . . . . 96 У р о к 2 8. Приведение дробей к общему знаменателю  . . . . . . . . . . . 100 У р о к 2 9. Сравнение дробей с разными знаменателями  . . . . . . . . . 103

Содержание                                                                                                         491

У р о к 3 0. Сравнение дробей с разными знаменателями  . . . . . . . . . 108

У р о к 3 1. Сравнение, сложение и вычитание дробей с разными

знаменателями  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111

У р о к 3 2. Сравнение, сложение и вычитание дробей с разными

знаменателями  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114

У р о к 3 3. Сравнение, сложение и вычитание дробей с разными

знаменателями  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117

У р о к 3 4. Сравнение, сложение и вычитание дробей с разными

знаменателями  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120 У р о к 3 5. Контрольная работа № 2  . . . . . . . . . . . . . . . . . . . . . . . . . . . 122 У р о к 3 6. Сложение и вычитание смешанных чисел  . . . . . . . . . . . . 123

У р о к 3 7. Сложение и вычитание смешанных чисел  . . . . . . . . . . . . 126

У р о к 3 8. Сложение и вычитание смешанных чисел  . . . . . . . . . . . . 129

У р о к 3 9. Сложение и вычитание смешанных чисел  . . . . . . . . . . . . 131

У р о к 4 0. Сложение и вычитание смешанных чисел  . . . . . . . . . . . . 134

У р о к 4 1. Сложение и вычитание смешанных чисел  . . . . . . . . . . . . 136 У р о к 4 2. Контрольная работа № 3  . . . . . . . . . . . . . . . . . . . . . . . . . . . 138

§ 3. Умножение и деление обыкновенных дробей

У р о к 4 3. Умножение дробей  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140

У р о к 4 4. Умножение дробей  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143

У р о к 4 5. Умножение дробей  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146

У р о к 4 6. Умножение дробей  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149 У р о к 4 7. «Счастливый случай» (урок-игра)  . . . . . . . . . . . . . . . . . . . . 152 У р о к 4 8. Нахождение дроби от числа  . . . . . . . . . . . . . . . . . . . . . . . . . 156

У р о к 4 9. Нахождение дроби от числа  . . . . . . . . . . . . . . . . . . . . . . . . . 160

У р о к 5 0. Нахождение дроби от числа  . . . . . . . . . . . . . . . . . . . . . . . . . 162

У р о к 5 1. Нахождение дроби от числа  . . . . . . . . . . . . . . . . . . . . . . . . . 166

У р о к 5 2. Применение распределительного свойства 

умножения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 168

У р о к 5 3. Применение распределительного свойства 

умножения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171

У р о к 5 4. Применение распределительного свойства 

умножения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173

У р о к 5 5. Применение распределительного свойства 

умножения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176

У р о к 5 6. Применение распределительного свойства 

умножения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 179 У р о к 5 7. Контрольная работа № 4  . . . . . . . . . . . . . . . . . . . . . . . . . . . 182

У р о к 5 8. Взаимно обратные числа  . . . . . . . . . . . . . . . . . . . . . . . . . . . 183

У р о к 5 9. Взаимно обратные числа  . . . . . . . . . . . . . . . . . . . . . . . . . . . 186 У р о к 6 0. Деление  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189

У р о к 6 1. Деление  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191

У р о к 6 2. Деление  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 193

У р о к 6 3. Деление  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 197

У р о к 6 4. Деление  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 199 У р о к 6 5. Контрольная работа № 5  . . . . . . . . . . . . . . . . . . . . . . . . . . . 201 У р о к 6 6. Нахождение числа по его дроби  . . . . . . . . . . . . . . . . . . . . . 202

492                                                                                                        Содержание

У р о к 6 7. Нахождение числа по его дроби  . . . . . . . . . . . . . . . . . . . . . 205

У р о к 6 8. Нахождение числа по его дроби  . . . . . . . . . . . . . . . . . . . . . 208

У р о к 6 9. Нахождение числа по его дроби  . . . . . . . . . . . . . . . . . . . . . 210

У р о к 7 0. Нахождение числа по его дроби  . . . . . . . . . . . . . . . . . . . . . 213 У р о к 7 1. Дробные выражения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 216

У р о к 7 2. Дробные выражения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 219

У р о к 7 3. Дробные выражения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 221

У р о к 7 4. Контрольная работа № 6  . . . . . . . . . . . . . . . . . . . . . . . . . . . 224

§ 4. Отношения и пропорции

У р о к 7 5. Отношения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 225

У р о к 7 6. Отношения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228

У р о к 7 7. Отношения  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231

У р о к 7 8. Пропорции  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235

У р о к 7 9. Пропорции  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239

У р о к 8 0. Пропорции  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 243

У р о к 8 1. Пропорции  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 246

У р о к 8 2. Повторение, обобщение и закрепление пройденного

материала за II полугодие  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 248

У р о к 8 3. Прямая и обратная пропорциональные зависимости  . . . 252

У р о к 8 4. Прямая и обратная пропорциональные зависимости  . . . 257

У р о к 8 5. Прямая и обратная пропорциональные зависимости  . . . 261

У р о к 8 6. Контрольная работа № 7  . . . . . . . . . . . . . . . . . . . . . . . . . . . 264 У р о к 8 7. Масштаб  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 265

У р о к 8 8. Масштаб  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270 У р о к 8 9. Длина окружности и площадь круга  . . . . . . . . . . . . . . . . . . 273

У р о к 9 0. Длина окружности и площадь круга  . . . . . . . . . . . . . . . . . . 277

У р о к 9 1. Шар  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 282

У р о к 9 2. Шар  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 286

У р о к 9 3. Контрольная работа № 8  . . . . . . . . . . . . . . . . . . . . . . . . . . . 288

ГЛАВА II. РАЦИОНАЛЬНЫЕ ЧИСЛА

§ 5. Положительные и отрицательные числа

У р о к 9 4. Координаты на прямой  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 290

У р о к 9 5. Координаты на прямой  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 296

У р о к 9 6. Координаты на прямой  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 298 У р о к 9 7. Противоположные числа  . . . . . . . . . . . . . . . . . . . . . . . . . . . 302

У р о к 9 8. Противоположные числа  . . . . . . . . . . . . . . . . . . . . . . . . . . . 305 У р о к 9 9. Модуль числа  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 308 У р о к 1 0 0. Модуль числа  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 311 У р о к 1 0 1. Сравнение чисел  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 313

У р о к 1 0 2. Сравнение чисел  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 316

У р о к 1 0 3. Сравнение чисел  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 318 У р о к 1 0 4. Изменение величин  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320

У р о к 1 0 5. Изменение величин  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 322 У р о к 1 0 6. Контрольная работа № 9  . . . . . . . . . . . . . . . . . . . . . . . . . . 324

§ 6. Сложение и вычитание положительных и отрицательных чисел

У р о к 1 0 7. Сложение чисел с помощью координатной прямой  . . . 325

Содержание                                                                                                         493

У р о к 1 0 8. Сложение чисел с помощью координатной прямой  . . . 328

У р о к 1 0 9. Сложение отрицательных чисел  . . . . . . . . . . . . . . . . . . . . 330

У р о к 1 1 0. Сложение отрицательных чисел  . . . . . . . . . . . . . . . . . . . . 333 У р о к 1 1 1. Сложение чисел с разными знаками  . . . . . . . . . . . . . . . . 335

У р о к 1 1 2. Сложение чисел с разными знаками  . . . . . . . . . . . . . . . . 338

У р о к 1 1 3. Сложение чисел с разными знаками  . . . . . . . . . . . . . . . . 340

У р о к 1 1 4. Вычитание  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 342

У р о к 1 1 5. Вычитание  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 345

У р о к 1 1 6. Вычитание  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 347 У р о к 1 1 7. Контрольная работа № 10  . . . . . . . . . . . . . . . . . . . . . . . . . 350

§ 7. Умножение и деление положительных и отрицательных чисел

У р о к 1 1 8. Умножение  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 351

У р о к 1 1 9. Умножение  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 354

У р о к 1 2 0. Умножение  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 357 У р о к 1 2 1. Деление  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 359

У р о к 1 2 2. Деление  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 363

У р о к 1 2 3. Деление  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 365 У р о к 1 2 4. Рациональные числа  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 367

У р о к 1 2 5. Рациональные числа  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 369

У р о к 1 2 6. Свойства действий с рациональными числами  . . . . . . . 372

У р о к 1 2 7. Свойства действий с рациональными числами  . . . . . . . 375

У р о к 1 2 8. Свойства действий с рациональными числами  . . . . . . . 377

У р о к 1 2 9. Контрольная работа № 11  . . . . . . . . . . . . . . . . . . . . . . . . . 379

§ 8. Решение уравнений

У р о к 1 3 0. Раскрытие скобок  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 380

У р о к 1 3 1. Раскрытие скобок  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 384

У р о к 1 3 2. Раскрытие скобок  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 386

У р о к 1 3 3. Повторение и обобщение материала за III четверть

(урок-игра)  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 389 У р о к 1 3 4. Коэффициент  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 392

У р о к 1 3 5. Коэффициент  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 395 У р о к 1 3 6. Подобные слагаемые  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 398

У р о к 1 3 7. Подобные слагаемые  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 401

У р о к 1 3 8. Подобные слагаемые  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 404 У р о к 1 3 9. Контрольная работа № 12  . . . . . . . . . . . . . . . . . . . . . . . . . 406 У р о к 1 4 0. Решение уравнений  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 407

У р о к 1 4 1. Решение уравнений  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 411

У р о к 1 4 2. Решение уравнений  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 415

У р о к 1 4 3. Решение уравнений  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 417

У р о к 1 4 4. Контрольная работа № 13  . . . . . . . . . . . . . . . . . . . . . . . . . 419

§ 9. Координаты на плоскости

У р о к 1 4 5. Перпендикулярные прямые  . . . . . . . . . . . . . . . . . . . . . . . 420

У р о к 1 4 6. Перпендикулярные прямые  . . . . . . . . . . . . . . . . . . . . . . . 424 У р о к 1 4 7. Параллельные прямые  . . . . . . . . . . . . . . . . . . . . . . . . . . . . 426

У р о к 1 4 8. Параллельные прямые  . . . . . . . . . . . . . . . . . . . . . . . . . . . . 429 У р о к 1 4 9. Координатная плоскость  . . . . . . . . . . . . . . . . . . . . . . . . . . 432

494                                                                                                        Содержание

У р о к 1 5 0. Координатная плоскость  . . . . . . . . . . . . . . . . . . . . . . . . . . 435

У р о к 1 5 1. Координатная плоскость  . . . . . . . . . . . . . . . . . . . . . . . . . . 437

У р о к 1 5 2. Столбчатые диаграммы  . . . . . . . . . . . . . . . . . . . . . . . . . . . 439

У р о к 1 5 3. Столбчатые диаграммы  . . . . . . . . . . . . . . . . . . . . . . . . . . . 442 У р о к 1 5 4. Графики  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 444

У р о к 1 5 5. Графики  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 446

У р о к 1 5 6. Графики  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 447

У р о к 1 5 7. Контрольная работа № 14  . . . . . . . . . . . . . . . . . . . . . . . . . 450

ПОВТОРЕНИЕ

У р о к 1 5 8. Делимость чисел  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 451

У р о к 1 5 9. Делимость чисел  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 453

У р о к 1 6 0. Сложение и вычитание дробей с разными

знаменателями  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 456

У р о к 1 6 1. Сложение и вычитание дробей с разными

знаменателями  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 458

У р о к 1 6 2. Умножение и деление обыкновенных дробей  . . . . . . . . 460

У р о к 1 6 3. Умножение и деление обыкновенных дробей  . . . . . . . . 462

У р о к 1 6 4. Отношения и пропорции  . . . . . . . . . . . . . . . . . . . . . . . . . . 465

У р о к 1 6 5. Отношения и пропорции  . . . . . . . . . . . . . . . . . . . . . . . . . . 466 У р о к 1 6 6. Решение задач  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 469

У р о к 1 6 7. Сложение и вычитание положительных

и отрицательных чисел  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 472

У р о к 1 6 8. Сложение и вычитание положительных

и отрицательных чисел  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 474

У р о к 1 6 9. Умножение и деление положительных

и отрицательных чисел  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 477

У р о к 1 7 0. Умножение и деление положительных

и отрицательных чисел  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 480 У р о к 1 7 1. Контрольная работа № 15  . . . . . . . . . . . . . . . . . . . . . . . . . 482 У р о к 1 7 2. Решение задач и уравнений . . . . . . . . . . . . . . . . . . . . . . . . 482

У р о к 1 7 3. Решение задач и уравнений . . . . . . . . . . . . . . . . . . . . . . . . 484

У р о к 1 7 4. Координаты на плоскости  . . . . . . . . . . . . . . . . . . . . . . . . . 486

Литература  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 489