Повторение раздела_Методические рекомендации к уроку №8

Методические рекомендации к проведению урока

Тема урока: Повторение раздела «Элементы статистики»

Тип урока: урок-повторение

Цели обучения:

8.3.3.1

представлять результаты выборки в виде интервальной таблицы частот;

8.3.3.2

представлять данные интервальной таблицы частот в виде гистограммы частот;

8.3.3.3

знать определение накопленной частоты;

8.3.3.4

анализировать информацию по статистической таблице, полигону частот, гистограмме;

8.3.3.5

знать определения и формулы для вычисления дисперсии и стандартного отклонения;

Цели урока:

Учащиеся могут

·         представлять данные в виде интервальной таблицы;

·         строить полигон и гистограмму частот;

·         находить накопленные частоты по данным статистической таблицы;

·         находить среднее арифметическое, медиану, моду, размах числового ряда;

вычислять дисперсию и стандартное отклонение.

Структура урока

1.    Организационный момент. Целеполагание.

2.    Мотивационный момент.

3.    Фронтальный опрос.

4.    Решение задач.

5.    Подведение итогов урока. Рефлексия.

Теоретический материал к уроку, определения к понятиям и др.

Интервальные ряды данных изображают с помощью гистограммы. Гистограмма представляет собой ступенчатую фигуру, составленную из сомкнутых прямоугольников.

Гистограмма отображает распределение отдельных измерений параметров изделия или процесса.

Каждый столбец указывает на частоту появления значений параметров в выбранном диапазоне, а количество столбцов – на число выбранных диапазонов.

Важное преимущество гистограммы заключается в том, что она позволяет наглядно представить тенденции изменения измеряемых параметров качества объекта.

Для наглядного изображения соотношения между частями исследуемой выборки удобно использовать круговые диаграммы.

В некоторых задачах таблицу частот удобно дополнить еще одной характеристикой, получившей название накопленной частоты. Накопленная частота показывает, какая доля элементов выборки не превышает данного значения. Накопленные частоты получаются из частот накопительным суммированием - отсюда их название. Последняя накопленная частота всегда равна 1. Накопленные частоты, так же, как и относительные, иногда измеряют в процентах.

Меры центральной тенденции.

МОДА числового ряда – это число, которое встречается в этом ряду наиболее часто.

МЕДИАНА числового ряда – это число этого ряда (или полусумма двух его чисел), слева и справа от которого на числовой прямой лежит одинаковое количество членов ряда (для нахождения медианы ряд должен быть ранжирован).

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ – сумма всех элементов ряда, деленная на их количество.

Меры рассеивания.

РАЗМАХ – это разность наибольшего и наименьшего значений ряда данных

ДИСПЕРСИЯ – среднее арифметическое квадратов отклонений от среднего значения называется в статистике набора чисел.

Есть другой способ вычисления дисперсии: нужно сначала вычислить среднее арифметическое самих чисел, затем — среднее арифметическое их квадратов, и наконец, из среднего арифметического квадратов вычесть квадрат среднего арифметического. Учитель вводит новую формулу для вычисления дисперсии числового ряда:

СРЕДНЕЕ КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ (СТАНДАРТНОЕ ОТКЛОНЕНИЕ) равно квадратному корню из дисперсии

.

Среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран решения и ответы к предложенным заданиям. Поэтому при показе презентации следует делать паузы после демонстрации заданий и постановки вопросов, давая учащимся время на их выполнение и обдумывание ответов.

Дополнительные методические рекомендации по организации урока.

При выполнении некоторых заданий целесообразно предложить учащимся использовать калькулятор, такой вид заданий отмечен следующим изображением: .

Дополнительные разноуровневые (на дифференциацию) задания.

Базовый уровень

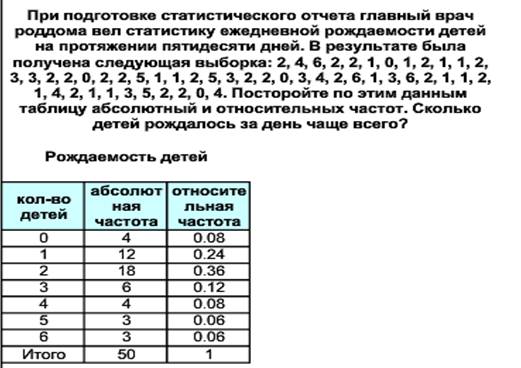
Продвинутый уровень

Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, взаимооценивание, оценивание учителем по критериям). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Ответы к заданиям будут полезны для организации самооценивания или взаимооценивания учащихся.

Критерии оценивания к каждому блоку заданий прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Ответы к приложению 1.

Задание 1. 7,9. Решение: число членов ряда чисел увеличили на 2, т. е. n₁ = n + 2 = 8 + 2 = 10, а сумму членов ряда чисел увеличили на 15 + 16 = 31. Значит, новая сумма равна 8 × 6 + 31 = 79. Поэтому среднее арифметическое нового ряда чисел равно .

Задание 2. [8; +¥). Решение: после ранжирования (упорядочения) данного ряда чисел в зависимости от значений х будет получен один из следующих рядов:

а) х, 6, 7, 8, 9, если х < 6;

б) 6, х, 7, 8, 9, если 6 £ х < 7;

в) 6, 7, х, 8, 9, если 7 £ х < 8;

г) 6, 7, 8, х, 9, если 8 £ х < 9;

д) 6, 7, 8, 9, х, если х ³ 9.

Найдем для каждого из этих пяти рядов его медиану: 7; 7; х, 8; 8. Получаем, что медиана равна 8 при х ³ 8.

Задание 3.

 –10; 59. Решение: размах ряда определяется формулой А = х_max – х_min.

Возможны два решения:

а) если считать х_max = 40, то х_min = х_max – А, х_min = 40 – 50 = –10.

б) если считать х_min = 9, то х_max = х_min + А, х_max = 9 + 50 = 59.

Задание 4. 70; 140. Решение: согласно условию, у = 2х, тогда среднее арифметическое заданного ряда . Решим уравнение , отсюда, х = 70. Второе число 2х = 2 × 70 = 140.

Задание 5.

Задание 6.

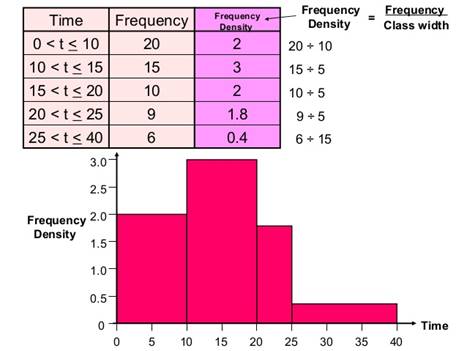
Задание 7.

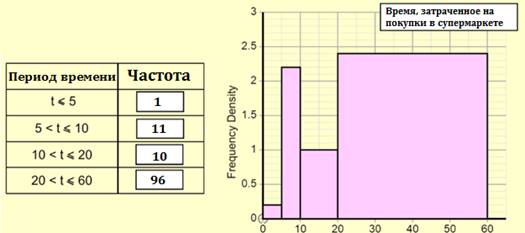
Задание 8.

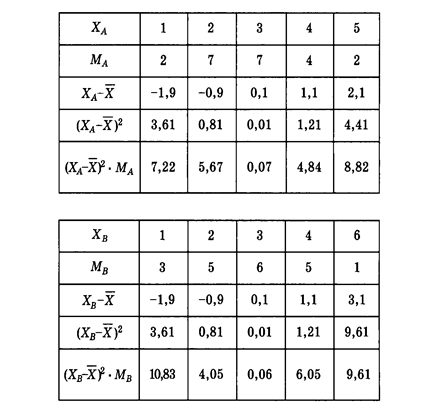
Список полезных ссылок и литературы.

Алгебра. Элементы статистики и теории вероятностей. 7-9 классы. Макарычев Ю. Н., Миндюк Н. Г. / Под.ред. Теляковского С. А. 3-е изд. - М.: Просвещение, 2005. - 78 с. 

Алгебра и начала математического анализа.  10-11 классы. Мордкович А.Г. Учебник. — 10-е изд., стер. — М.: Мнемозина, 2009. — 399 с.

https://youclever.org/book/elementy-statistiki-1

https://videouroki.net/video/43-eliemienty-statistiki.html

Скачано с www.znanio.ru