Практическая работа на тему: " Последовательности. Нахождение пределов числовых последовательностей"

Практическая работа №1

Тема: «Последовательности. Нахождение предела числовой последовательности»

Цель: Научиться определять свойства и вычислять пределы числовой последовательности, а также использовать при вычислениях первый и второй замечательный пределы.

Оборудование: ручка, методические рекомендации по выполнению работы.

Методические рекомендации по выполнению практической работы:

Задание №1. Определить, ограничена ли последовательность:

а) ;      б)

Решение:

а)

Пусть , таким образом, данная последовательность ограничена снизу числом 4, значит m = 4 – нижняя граница последовательности с общим членом .

б) .

Найдем несколько первых членов данной последовательности:

Замечаем, что все члены нашей последовательности уменьшаются и стремятся к нулю: , это означает, что все члены последовательности находятся между 0 и , тогда данная последовательность ограничена и снизу m = 0 (нижняя граница) и M =  (верхняя граница)

Задание №2. Определить, монотонна ли последовательность:

а) ;    б)

Решение:

а) Рассмотрим последовательность с общим членом   Найдем несколько первых членов данной последовательности:

Так как между членами последовательности выполняется неравенство:

, то по определению получаем возрастающую последовательность.

б) Рассмотрим последовательность с общим членом   Найдем несколько первых членов данной последовательности:

Так как между членами последовательности выполняется неравенство:

, то по определению получаем убывающую последовательность.

Задание №3. Вычислить пределы последовательностей:

а) ,   б) ;   в) ;   г) ;

д) .

Решение:

а) ,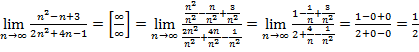

б)

=.

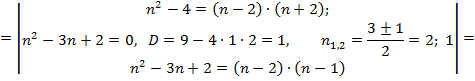
в)

=

г)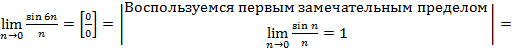

д)

.

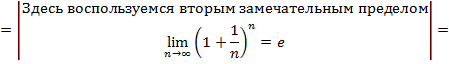
Задание №4. Найти сумму геометрической прогрессии:

а)  ; б)

Решение:

а)  .

В данной геометрической последовательности . Поскольку знаменатель прогрессии удовлетворяет неравенству , то справедлива формула для суммы геометрической прогрессии: . Значит, искомая сумма равна

б)

Здесь имеем, что , так как , то справедлива формула для суммы геометрической прогрессии: . Значит, искомая сумма равна

Задания для самостоятельной работы:

Контрольные вопросы (ответьте письменно):

1.      Запишите определение ограниченной сверху последовательности.

2.      Запишите определение ограниченной снизу последовательности.

3.      Запишите определение ограниченной последовательности.

4.      Запишите определение возрастающей последовательности.

5.      Запишите определение убывающей последовательности.

6.      Запишите определение монотонной последовательности.

7.      Запишите формулу для первого замечательного предела.

8.      Запишите формулу для второго замечательного предела.

9.      Запишите формулу для суммы геометрической прогрессии.

10.