Практическая работа специальности 09.02.01.

Практическая работа № 9

Тема: «Решение задач по комбинаторным формулам»

Цель: закрепление правил комбинаторики и основных формул, овладение способами решения задач на определение количество выборок.

Теория

Основные понятия комбинаторики.

При решении комбинаторной задачи следует четко определять вид комбинации элементов, т.е. операцию комбинаторики, вид соединения.

Комбинаторика - раздел математики, изучающий задачи выбора и расположения элементов из некоторого множества в соответствии с заданными правилами. распространенными задачами комбинаторики являются задачи о числе размещений, перестановок и сочетаний элементов.

Одно из важных правил комбинаторики - правило умножения:

Если требуется выполнить одно за другим к действий и 1ое действие можно выполнить n₁ способами, 2 ое – n₂ способами, и т.д. До его действия, которое выполняется n_к способами, то все действия к можно вместе выполнить

 способами

В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.

Предварительно познакомимся с понятием факториала.

Произведение всех натуральных чисел от 1 до n включительно называют n - факториалом и пишут .

Перестановки.

Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.

Число перестановок можно вычислить по формуле

 или с помощью факториала:

Запомним, что 0!=1 и 1!=1.

Размещения

Размещениями из m элементов в n в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком из расположения.

Число размещений можно вычислить по формуле

,

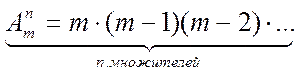Запишем эту формулу в факториальной форме:

.

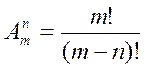Сочетания.

Сочетаниями называются все возможные комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом (здесь m и n-натуральные числа, причем n  m).

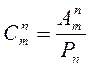
Используя для чисел размещений и перестановок факториальные формулы, получим:

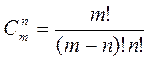
Ход работы

          1 Решите задачи

1.      сколько различных пятизначных чисел можно составить из цифр 1, 3, 5, 7, 9 при условии, что ни одна цифра в числе не повторяется?

2.      Сколько существует вариантов распределения трех призовых мест, если в розыгрыше участвуют 7 команд?

3.      Сколькими способами можно выбрать двух студентов на конференцию, если в группе 33 человека?

4.      Сколько четырехзначных чисел, делящихся на 5, можно составить из цифр 0, 1, 2, 5, 7, если каждое число не должно содержать одинаковых цифр?

5.      Из группы в 15 человек должны быть выделены бригадир и 4 члена бригады. Сколькими способами это можно сделать?

6.      Буквы азбуки Морзе состоят из символов (точек и тире). Сколько букв можно изобразить, если потребовать, чтобы каждая буква содержала не более пяти символов?

7.      Сколькими способами можно составить четырехцветные ленты из семи лент.

8.     Семь девушек водят хоровод. Сколькими различными способами они могут встать в круг?

9.    Из 7 человек надо выбрать 5 человек и разместить их на пяти занумерованных стульях (по 1 человеку на стуле). Сколькими способами это можно сделать?

10.  Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

2 Вычислите количество комбинаций

1                   Сколькими способами можно выбрать две буквы: гласную и согласную из слова «здание»?

2                   Бросают игральную кость с 6 гранями и запускают волчок, имеющий 8 граней. Сколькими различными способами могут они упасть?

3                   Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, если имеется материя 6 различных цветов?

4                   Из состава конференции, на которой присутствуют 52 человека, надо избрать президиум в составе 5 человек и делегацию в составе 3 человек. Сколькими способами может быть произведен выбор, если члены президиума не могут войти в состав делегации?

5                   Сколькими способами можно выбрать две буквы: гласную и согласную из слова «камзол»?

6                   Всего в группе 45 студентов. Из них в футбольной секции состоят 25 человек, в баскетбольной – 30, в шахматной – 28. 16 студентов участвуют в футбольной и баскетбольной секции, 18 – в футбольной и шахматной, и 17 – в баскетбольной и шахматной. Сколько студентов участвуют во всех трех секциях?

7                   Маша на свой день рождения пригласила в гости трех лучших подруг - Дашу, Глашу и Наташу. Когда все собрались, то по случаю дня рождения Маши решили обняться - каждая пара по одному разу. Сколько получилось разных пар?

8                   На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?

9                   Из 12 слов мужского рода, 9 женского и 10 среднего нужно выбрать по одному слову каждого рода. Сколькими способами может быть сделан этот выбор?

10              Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры не могут повторяться?

11              Имеется 5 видов конвертов без марок и 4 вида марок. Сколькими способами можно выбрать конверт с маркой для посылки письма?

12              Перед нами 10 закрытых замков и 10 похожих ключей к ним. К каждому замку подходит только один ключ, но ключи смешались. Возьмем один из замков, назовем его первым и попробуем открыть его каждым из 10 ключей. В лучшем случае он откроется первым же ключом, а в худшем - только десятым. Сколько нужно в худшем случае произвести проб, чтобы открыть все замки?

13              В букинистическом магазине лежат 6 экземпляров романа И.С. Тургенева «Рудин», 3 экземпляра его же романа «Дворянское гнездо» и 4 экземпляра романа «Отцы и дети». Кроме того, есть 5 томов, содержащих романы «Рудин» и «Дворянское гнездо», 7 томов, содержащих романы «Дворянское гнездо» и «Отцы и дети», 3 тома, содержащие романы «Рудин»  и «Отцы и дети», и 5 томов, содержащих все три романа. Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из этих романов?

14              Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?

15