Практическая работа специальности 09.02.01.

Практическое занятие № 11

Решение задач по теме: «Бином Ньютона»

Цель: научиться применять формулу бинома Ньютона, понять, как строится треугольник Паскаля для нахождения коэффициентов бинома Ньютона.

Теория

Бином Ньютона:

Свойства Бинома Ньютона:

1.     Число слагаемых на 1 больше степени бинома.

2.     Коэффициенты находятся по треугольнику Паскаля.

3.     Коэффициенты симметричны.

4.     Если в скобке знак минус, то знаки + и – чередуются.

5.     Сумма степеней каждого слагаемого равна степени бинома.

Ход работы

1. Написать разложение по формуле бинома Ньютона и упростить:

а)  ;  б) 

2.Разложить по формуле бинома Ньютона и упростить. Коэффициенты разложения найти, используя треугольник Паскаля:

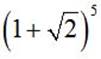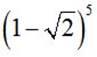а) (0,5а+b)⁷         б) ;         в) ;         г)  

3. Найдите два средних члена разложения

4. В биномиальном разложении 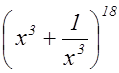 найти член разложения, не содержащий х.

5. Решить уравнение

6. Найти алгебраическую сумму коэффициентов многочлена относительно x, получаемого в разложении бинома Ньютона  (3x – 4)¹⁷. 

7. Найти 13-й член разложения бинома

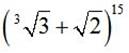
8. Построить треугольник Паскаля и найти  
коэффициенты разложения бинома Ньютона (a +2 b)⁹.

9. Найти номер члена разложения бинома , не содержащего х.

10. Найти пятый член разложения бинома .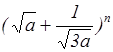

11. Найти сумму биномиальных коэффициентов членов, стоящих на нечетных местах в разложении бинома , если биномиальный коэффициент третьего члена на 9 больше биномиального коэффициента второго члена.

12. Сколько членов разложения бинома  являются целыми числами?

13. Найти седьмой член разложения бинома 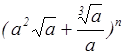, если биномиальный коэффициент третьего члена равен 36

14. Вычислить сумму .

15. Найти алгебраическую сумму коэффициентов многочлена относительно х, получаемого в разложении бинома .

16. Сумма нечетных биномиальных коэффициентов разложения 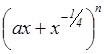 равна 512. Найти слагаемое, не содержащее х.

17. При каких значениях х четвертое слагаемое разложения  больше двух соседних с ним слагаемых?

18.При каком значении х четвертое слагаемое разложения  в двадцать раз больше m, если биномиальный коэффициент четвертого слагаемого относится к биномиальному коэффициенту второго слагаемого как 5 : 1?

19.С помощью свойства элементов строки треугольника Паскаля найти сумму         

20. В какую наибольшую степень следует возвести бином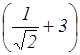, чтобы отношение четвертого слагаемого разложения к третьему было равно ?