
Практическое занятие № 13
Решение задач по теме: «Графы». Определение типов графов и их характеристик.
Цель: закрепить умения выполнять операций над графами.
Теория
Графы являются существенным элементом математических моделей в самых разнообразных областях науки и практики. Они помогают наглядно представить взаимоотношения между объектами или событиями в сложных системах. Многие алгоритмические задачи дискретной математики могут быть сформулированы как задачи, так или иначе связанные с графами, например, задачи, в которых требуется выяснить какие-либо особенности устройства графа, или найти в графе часть, удовлетворяющую некоторым требованиям, или построить граф с заданными свойствами.
Легко найти примеры графов в самых разных областях науки и практики. Сеть дорог, трубопроводов, электрическая цепь, структурная формула химического соединения, блок-схема программы
Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту. Многие математические доказательства также упрощаются, приобретают убедительность, если пользоваться графами. Для решения логических задач удобно использовать графы.
Графы – это рисунки, которые состоят из точек и линий, соединяющих эти точки.
Каждая пара точек в графе может быть соединена линиями. Линия указывает на связь между двумя точками.
Точки называются вершинами графа, а линиями рёбрами.
Ребро может иметь направление, которое указывается стрелочкой.
У графа обязательно есть вершины.
Граф без рёбер называется пустым.
Дерево (граф) – это способ организации информации об отношениях между объектами.
Примеры различных графов приведены на рисунке.
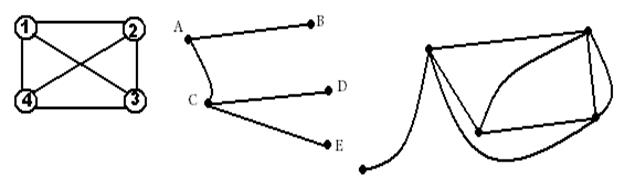
Слово «дерево» в теории графов означает граф, в котором нет циклов, то есть в котором нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину.
Графы, в которых не построены все возможные рёбра называется не полными графами.
Особым видом графа является дерево. Данная форма модели применяется тогда, когда элементы моделируемого объекта находятся в состоянии какого-либо подчинения и соподчинения, когда есть отношение иерархичности. Модель управления предприятием (школой, театральным коллективом и т. д.) очень удобно представлять в виде дерева.
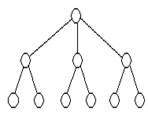
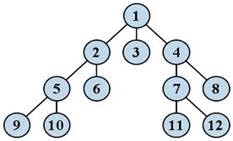
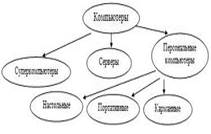
Описать граф — это значит, ответить на вопросы:
– Сколько вершин?
– Есть рёбра?
– Есть направление?
– Все ли вершины соединены рёбрами?
Ход работы
Задание 1
а) Нарисовать граф системы «Компьютер», содержащий следующие вершины: процессор, оперативная память, внешняя память, клавиатура, дисплей, принтер. Соединить их направленными линиями (стрелками), обозначающими отношение «передаёт информацию».
б) К построенному графу добавить пунктирные направленные линии, обозначающие отношение «управляет» (работой всех устройств управляет процессор).
Задание 2
Построить родословное дерево потомков Владимира Мономаха.
Потомки Владимира Мономаха.
Владимир Мономах умер в 1125 г. Он оставил четырёх сыновей: Мстислава (год смерти - 1132), Ярополка (1139), Вячеслава Туровского (1154) и Юрия Долгорукого (1157).
После Мстислава остались три сына: Изяслав Волынский (1154), Всеволод Новгородский (1138) и Ростислав Смоленский (1168).
У Изяслава Волынского был сын Мстислав (1170), у Мстислава - сын Роман (1205), у Романа - Даниил Галицкий (1264). Ростислав Смоленский имел четырех сыновей: Романа (1180), Рюрика (1215), Давида (1197) и Мстислава Храброго (1180).
После Романа Ростиславича остался сын Мстислав Киевский (1224), после Мстислава Храброго - сын Мстислав Удалой (1228).
Юрий Долгорукий имел трех сыновей: Андрея Боголюбского (1175), Михаила (1177) и Всеволода (1212).
Сыновьями Всеволода были Константин (1217), Юрий (1238) и Ярослав (1246).
У Ярослава Всеволодовича было три сына: Александр Невский (1263), Андрей Суздальский (1264) и Ярослав Тверской (1272).
Сыновья Александра Невского: Димитрий Переяславский (1294), Андрей Городецкий (1304) и Даниил Московский (1303).
У Андрея Суздальского был сын Василий (годы его жизни неизвестны), у Ярослава Тверского - сын Михаил (1318).
Глядя на полученное дерево, ответьте на вопрос: сколько поколений князей оно отражает?
Задание 3
Постройте матрицы смежности для графа а) и в) и матрицы инцидентности для графа б) и г).

Задание 4
Постройте графы, соответствующие каждой из матриц смежности:
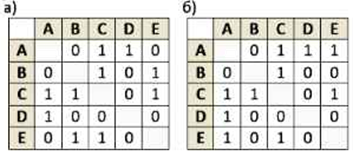
Задание 5
Постройте графы, соответствующие каждой из матриц инцидентности:
а)
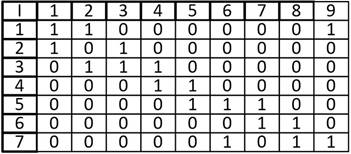
б)
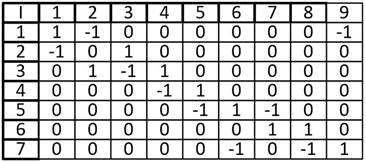
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.