Практическая работа специальности 15.02.05. «Техническая эксплуатация оборудования в торговле и общественном питании»

Министерство образования и науки Краснодарского края

Государственное бюджетное профессиональное образовательное учреждение

Краснодарского края

«Армавирский механико – технологический техникум»

Методическое пособие

для проведения

практического занятия

на тему:

«АКСОНОМЕТРИЧЕСКИЕ ОСИ. ПОКАЗАТЕЛИ ИСКАЖЕНИЯ»

по дисциплине: «Инженерная графика»

для студентов 2 курса

спец. 15.02.01, 15.02.05, 19.02.03, 19.02.06, 19.02.08, 19.02.09

очного и заочного отделения

Разработал преподаватель: Е.В. Игнатова

2016

1. ЦЕЛЬ РАБОТЫ

Познакомиться с видами аксонометрических проекций

2 ОБЩИЕ СВЕДЕНИЯ

Аксонометрические изображения широко применяются благодаря хорошей наглядности и простоте построений.

Изучение аксонометрических проекций способствует развитию пространственного воображения и образного мышления, которые необходимы в профессионализме любого техника, конструктора, архитектора, педагога и т. д.

Слово «аксонометрия» в переводе с греческого означает измерение по осям. Аксонометрический метод может сочетаться и с параллельным, и с центральным проецированием при условии, что предмет проецируется вместе с координатной системой.

Метод аксонометрического проецирования состоит в том, что изображаемый объект вместе с осями прямоугольных координат, жестко связанными с этим объектом пучком параллельных лучей, проецируется на одну плоскость П, которую называют плоскостью аксонометрических проекций (эту плоскость называют также картинной плоскостью).

В зависимости от направления проецирования лучей относительно плоскости П аксонометрические проекции делятся на косоугольные и прямоугольные(ортогональные).

1.1. Проецирование системы координат

Поскольку система координат, связанная с объектом, является базисной основой аксонометрической проекции, то вначале рассмотрим проецирование только одной системы осей координат на плоскость П.

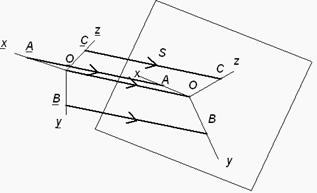
Рисунок 1. Аппарат проецирования

 На рис. 1 изображена пространственная система координат Oxyz, плоскость аксонометрических проекций П, на которую в направлении S проецируется эта система, и аксонометрическая проекция Oxyz данной системы координат. Ось х, у и z, полученные в результате такого проецирования называютсяаксонометрическими осями.

Если на осях пространственной системы взять произвольно точки А, В и С, то в аксонометрии им будут соответствовать точки А, В и С. Так как при параллельном косоугольном проецировании длина проекции отрезка прямой может быть больше, меньше или равна длине самого отрезка, то в общем случае отрезки ОА, ОВ и ОС, взятые на осях координат не будут равны отрезкам ОА, ОВ и ОС, полученным на аксонометрических осях, и степень неравенства этих отрезков выразится отношениями:

, , . 

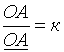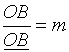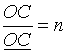Показатели отношений к, m и n будут называться в дальнейшем коэффициентами искажения. Таким образом, коэффициентом искажения по аксонометрической оси называется отношение длины проекции отрезка к длине самого отрезка, взятого на оси координат.

В зависимости от направления проецирования и положения осей координат относительно плоскости аксонометрических проекций коэффициенты искажения могут быть больше, меньше или равны единице. А это значит, что коэффициенты искажения при косоугольном проецировании могут изменяться в пределах от нуля до бесконечности ().

1.2. Виды аксонометрических проекций

Применяемые в отечественной конструкторской документации аксонометрические проекции стандартизованы в ГОСТ 2.317 – 69.

В зависимости от направления проецирования аксонометрические проекции делятся на косоугольные и прямоугольные. По признаку соответствия коэффициентов искажения между собой аксонометрические проекции можно разделить на изометрические, диметрические и триметрические. Если в аксонометрии все три коэффициента будут равны – k = m = n, то получается изометрическая (isos – одинаковый) проекция, т. е. проекция одинаковых коэффициентов по всем трем осям.

Если равны между собой будут два из коэффициентов искажения, а третий не равен им, то образуется диметрическая (di – двойной) проекция или аксонометрия одинаковых коэффициентов искажения по двум осям. В диметрии могут быть случаи когда ,  или .

Если же все три коэффициента будут различны – , то получается триметрическая (treis – три) проекция, т. е. проекция различных коэффициентов искажения по всем трем осям.

1.3. Аксонометрия точки

Возьмем в пространственной системе координат Oxyz точку А и спроецируем ее вместе с осями координат на плоскость П (рис. 2) Пусть положение точки А в этой системе определяется координатами Х_А, У_А и Z_А, т. е. числами, соответствующими отрезкам ОХ_А, ОУ_А и ОZ_А, длины которых равны расстояниям точки А от плоскостей координат П₃, П₂ и П₁. В аксонометрической проекции положения первичной А и вторичных А₁, А₂ и А₃ проекций точки Абудут определяться аксонометрическими координатами Х_А, У_А и Z_A, относительно системы аксонометрических осей Охуz. Если координаты Х_А, У_А и Z_Aсоответствующие отрезкам ОХ_А, ОУ_А и ОZ_А, выразить теми же единицами измерения, что и пространственные координаты, то числа Х_А, У_А и Z_A в общем случае будут отличаться от чисел Х_А, У_А и Z_А. При этом отношения их будут равны коэффициентам искажения по аксонометрическим осям:

Х_А: Х_А = k, У_А: У_А = m, Z_A: Z_A = n.                                        (1)

Отношения аксонометрических координат к пространственным у всех точек, взятых в системе Охуz, является постоянными и равными коэффициентам искажения k, m и n (рис. 2).

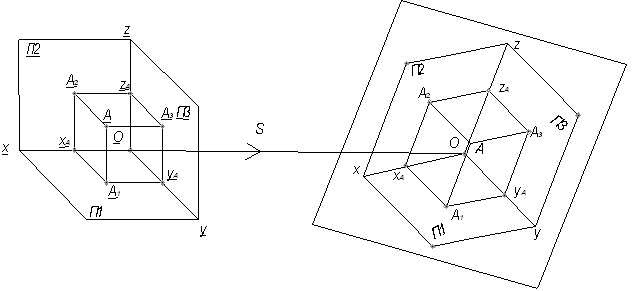
Рисунок 2. Пространственное построение точки в аксонометрической проекции

Теорема метрической определенности аксонометрии точки. При заданных аксонометрических осях и трех коэффициентах искажения положение точки в пространстве вполне определяется первичной и одной из вторичных ее аксонометрических проекций.

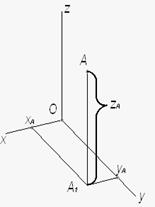
Рисунок 3. Построение точки в аксонометрической проекции

На рис. 3 изображена в аксонометрической проекции точка А. Имея первичную А и, например, горизонтальную вторичную А₁, проекции этой точки, а так же систему аксонометрических осей, можно простым построением (проведением прямых А₁Х_А и А₁У_А параллельно соответствующим осям) найти две аксонометрические координаты. Третья координата определяется отрезком, соединяющим первичную и вторичную проекции. Воспользовавшись полученными координатами Х_А, У_А и Z_A и значениями известных коэффициентов искажения, по формулам (1) можно вычислить пространственные координаты точки А:

,   ,  .

Прямоугольные координаты Х_А, У_А и Z_А вполне определяют положение точки в пространстве.

1.4. Аксонометрические оси

Три произвольные прямые, проходящие через одну точку, всегда можно считать аксонометрическими осями. Справедливость такого утверждения вытекает из теоремы Польке, которая гласит: «Любые три отрезка, расположенные в плоскости и выходящие из одной точки, можно считать параллельной проекцией трех равных, взаимно-перпендикулярных и выходящих из одной точки отрезков».

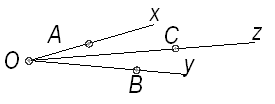
Рисунок 4. Точки на пространственной системе координат

Как видно, на произвольно взятых аксонометрических осях системы Охуz (рис. 4) можно, к тому же, отложить и произвольные отрезки ОА, ОВ и ОСсчитая их изображением трех равных отрезков, расположенных на осях пространственной системы прямоугольных координат Охуz.

Однако это не значит, что на осях любой системы Охуz можно задать произвольно три коэффициента искажения k, m и n. Эти коэффициенты находятся в строгой зависимости от направления проецирования и расположения осей координат относительно плоскости П, т. е. от взаимного расположения аксонометрических осей. Выбор коэффициентов искажения на произвольно взятых аксонометрических осях ограничивается строго определенными условиями. Более того, при некоторых значениях углов, образованных аксонометрическими осями, нельзя задаваться произвольным коэффициентом даже на одной из аксонометрических осей.

В общем же случае произвольно, в области значений от нуля до бесконечности, можно взять коэффициент искажения на одной оси, на второй взять также произвольно, но из области более ограниченных пределов, а на третьей оси коэффициент искажения определяется в зависимости от значений первых двух.

1.5. Стандартные косоугольные аксонометрические проекции

Государственный стандарт ГОСТ 2.317–69 рекомендует для применения в техническом черчении фронтальные изометрические, фронтальные диметрические и горизонтальные изометрические проекции.

Косоугольные аксонометрические проекции общего вида практически (как наглядные изображения) не применяются. Практическое применение имеют косоугольные проекции частных видов, которые получаются при параллельном расположении плоскости координат П₂ или П₁ относительно плоскости аксонометрических проекций П. В первом случае косоугольная аксонометрическая проекция называется фронтальной (рис. 5, а), во второмгоризонтальной (рис. 5, б).

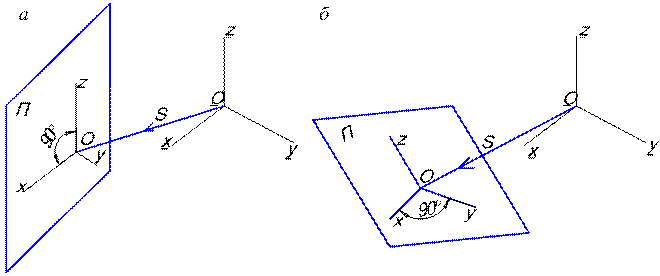
Рис. 5. Косоугольные проекции: а – фронтальная; б – горизонтальная

1.5.1. Фронтальная косоугольная изометрическая проекция

Оси Х и Z взаимно-перпендикулярны и коэффициенты искажения по ним равны единице (k=n=1) по той причине, что оси координат Х и Z параллельны плоскости П. Ось У образует с продолжением оси Х угол a (рис. 6, а). Этот угол и коэффициент искажения по оси У теоретически могут иметь любые значения, но государственный стандарт рекомендует как оптимальные a = 45^о и m=1. Допускается также применение фронтальных изометрических проекций с углом a, равным 30^о или 60^о.

 3 ЗАДАНИЕ

Вычертить в тетради оси различных видов аксонометрических проекций.

4 КОНТРОЛЬНЫЕ ВОПРОСЫ

1.     Как образуется аксонометрическая проекция?

2.     Какие виды аксонометрических проекций вам известны?

3.     Перечислите оси проекций.

4.     Какие показатели искажения на осях в прямоугольной изометрической проекции?

Скачано с www.znanio.ru