Практическая работа специальности 15.02.05. «Техническая эксплуатация оборудования в торговле и общественном питании»

Министерство образования, науки и молодежной политики Краснодарского края

Государственное бюджетное профессиональное образовательное учреждение

Краснодарского края

«Армавирский механико – технологический техникум»

Методическое пособие

для проведения

практического занятия

на тему:

«ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТЕЙ ТЕЛ. ПРОЕЦИРОВАНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ.»

по дисциплине: «Инженерная графика»

для студентов 2 курса

спец. 09.02.01, 15.02.01, 15.02.05, 19.02.03, 19.02.06, 19.02.08, 19.02.09

очного и заочного отделения

Разработал преподаватель: Е.В. Игнатова

2021

1 ЦЕЛЬ РАБОТЫ:

1.1 Получить представление о прямоугольном проецировании.

1.2 Построить комплексные чертежи проекций геометрических тел

1.3 Найти проекции точек, принадлежащих поверхности данного тела.

1.4 Изобразить геометрические тела в аксонометрии.

2 ОБЩИЕ СВЕДЕНИЯ

2.1 Проекции геометрических тел

Формы деталей, встречающихся в технике, представляют собой сочетание различных геометрических тел или их частей.

Для выполнения и чтения чертежей деталей нужно знать, как правильно изображаются геометрические тела.

Построение проекции прямого цилиндра с вертикально осью (рисунок 4) начинают с изображения основания цилиндра, представляющего собой круг.

Поскольку круг расположен параллельно плоскости Н и, следовательно, изображается на ней без искажений, его горизонтальная проекция, также круг, а фронтальная и продольная - горизонтальные отрезки прямых, равные диаметру круга. Фронтальная и профильная проекции цилиндра очерчиваются отрезками прямых, представляющими проекции его основания и крайних образующих. На всех видах проводят оси симметрии. Размеры цилиндра определяются диаметром его основания и высотой.

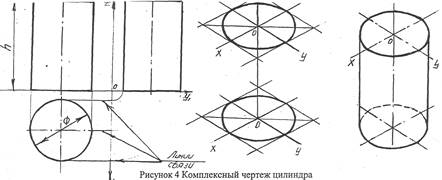
Фронтальная и профильная проекции одинаковы, поэтому в данном случае профильная проекция лишняя. Чертежи всех геометрических тел будут выполнены в трех видах лишь с той целью, чтобы показать, какие проекции эти тела имеют.

Одно изображение конуса вращения (рисунок 5) сходно с изображением цилиндра. Так, на виде сверху конус представляет собой круг. На нем наносят центровые линии. Диаметр круга равен диаметру основания конуса. Два других изображения конуса - равнобедренные треугольники. На этих проекциях также наносят оси симметрии. Для конуса указывают диаметр его основания и высоту.

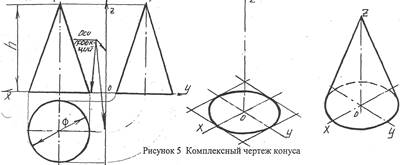
Построение изображений правильной треугольной призмы (рисунок 6) следует начинать с основания равностороннего треугольника. На фронтальной плоскости проекции задняя грань призмы изображается в натуральную величину, две передние - с искажением ширины. На профильной проекции ширина прямоугольника равна высоте фигуры основания призмы. На горизонтальной и фронтальной проекциях проводят осевые линии, на профильной проекции ось симметрии отсутствует. Для правильной треугольной призмы указывают ее высоту, длину стороны основания и угол.

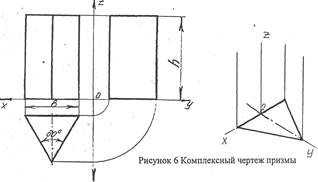
Построение прямоугольных проекций правильной шестиугольной призмы (рисунок 7) также начинают с вычерчивания вида сверху, который представляет собой правильный шестиугольник. На главном виде средняя грань изображается в натуральную величину, а ширина боковых граней искажена. На виде сбоку грани изображаются искаженными по ширине. Размеры правильной шестиугольной пирамиды определяют ее высотой и шириной, равной удвоенной длине стороны основания.

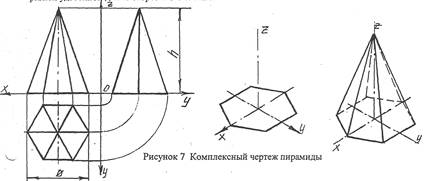
На чертежах (рисунки 4,5,6,7) приведены оси проекции х, у, z, а изображения соединены между линиями связи. Горизонтальная и профильная проекции соединены линями связи при помощи дуг с центром в точке 0 пересечения осей.

Необходимость в проведении линий связи и вспомогательных дуг возникает при построении недостающих проекций и при выполнении чертежей, на которых требуется определить проекции точек.

2.2 Проекции точки, лежащей на поверхности тела

Для того, чтобы при выполнении чертежей строить проекции отдельных элементов деталей, необходимо уметь находить на всех изображениях чертежа проекции отдельных точек.

Если на чертеже предмета дана одна проекция точки, то прежде надо найти проекции поверхности, на которой расположена эта точка.

На рисунке 8 изображен цилиндр, на фронтальной проекции которого задана проекция точки А, лежащей на видимой части его поверхности. Чтобы найти горизонтальную проекцию точки А, рассуждают так: точка лежит на поверхности цилиндра, горизонтальная проекция которой - окружность. Значит и проекция точки, лежащей на этой поверхности, будет лежать на окружности. Проводят линию связи и на пересечении ее с окружностью отмечают искомую точку а. Третью проекцию а" находят на пересечении линий связи.

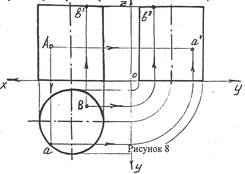
Если же точка В, лежащая на верхнем основании цилиндра, задана своей горизонтальной проекцией, то проводят линии связи до пересечения с отрезками прямых, изображающих фронтальную и профильную проекции верхнего основания цилиндра.

На рисунке 9 дана фронтальная проекция а точки, лежащей на видимой части поверхности конуса. Для нахождения горизонтальной проекции через точку а' проводят фронтальную проекцию вспомогательной прямой, проходящую через точку А и вершину конуса. Получают точку в' - проекцию точки встречи проведенной прямой с основанием конуса. Имея фронтальные проекции точек, лежащих на прямой, можно найти их горизонтальные проекции. Горизонтальная проекция S вершины конуса известна. Точка в лежит на окружности основания. Через эти точки проводят отрезок прямой и переносят на него (как показано стрелкой) точку а", получая точку а. Третья проекция а точки А находится на пересечении линий связи.

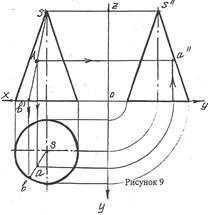
В качестве вспомогательной линии, проходящей через точку А, берут не прямую, как в первом случае, а окружность. Эта окружность образуется, если в точке А пересечь плоскостью, параллельной основанию. Фронтальная проекция этой окружности изобразиться отрезком прямой, так как плоскость окружности перпендикулярна фронтальной плоскости проекции. Горизонтальная проекция окружности имеет диаметр, равный длине отрезка. Описав окружность указанного диаметра, проводят из точки, а линию связи до пересечения с вспомогательной окружностью, так как горизонтальная проекция, а точки А лежит на вспомогательной линии, т.е. на построенной окружности. Третью проекцию, а" точки А находят на пересечении линий связи.

Таким же приемом можно найти проекции точки, лежащей на поверхности, например, пирамиды. Разница будет в том, что при ее пересечении горизонтальной плоскостью образуется не окружность, а фигура, подобная основанию.

3 ПРИМЕНЯЕМЫЕ ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

Готовальня, треугольники, линейка, карандаши и др.

4 ХОД РАБОТЫ

4.1 На А3 формате по двум заданным проекциям геометрического тела (см. задание) найти третью проекцию на пересечении линий связи.

4.2 Построить принадлежащие их поверхностям точки А, В (по заданию).

4.3 Найти недостающие проекции этих точек.

4.4 Построить размеры.

4.5 Построить аксонометрические проекции геометрических тел (см. рисунок 4,5,6,7)

4.6 Заполнить основную надпись.

4.7 Проверить правильность выполнения комплексного чертежа и аксонометрии.

5 КОНТРОЛЬНЫЕ ВОПРОСЫ:

5.1 Какие плоскости проекций вам известны?

5.2 В какой последовательности строят проекции прямого кругового цилиндра и правильной шестигранной призмы, основания которых расположены на фронтальной плоскости проекции?

5.3 Какими приемами определяют недостающие проекции точек, лежащих на поверхностях конуса, цилиндра?

5.4 Чем отличается пирамида от призмы?

5.5 В какой последовательности следует выполнять графическую работу?

5.6