Способы проецирования

7.1. Многообразие геометрических форм в природе. На уроках математики вы уже познакомились с некоторыми геометрическими фигурами. Под фигурой понимают любую совокупность (множество) точек. Всякую сложную фигуру можно разделить на более простые.

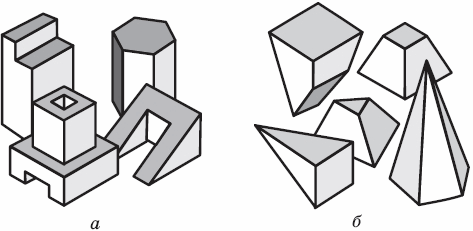
Если все точки фигуры лежат в одной плоскости, фигуру называют плоской: треугольник, квадрат и др. Совокупность точек, расположенных в пространстве, образует пространственную фигуру: куб, цилиндр и др. Фигуры в пространстве называют телами.

Предметы, которые нас окружают, детали машин имеют, как правило, сложную реальную геометрическую форму. Однако, присмотревшись к ним внимательно, можно заметить, что некоторые из них состоят из одного или нескольких простых геометрических тел или их видоизмененных частей. Такими геометрическими телами, образующими форму предметов, являются призмы (рис. 22, а), пирамиды (рис. 22, б), цилиндры (рис. 23, а), конусы (рис. 23, б), шары и др.

Форма каждого геометрического тела имеет свои характерные признаки. По ним мы отличаем призму от цилиндра, пирамиду от конуса и т. п. Эти признаки используются и при построении чертежей геометрических тел или состоящих из них предметов и деталей. Однако, прежде чем выполнять такие чертежи, выясним, какие правила положены в основу способов их построения.

1. Какие геометрические тела вам известны?
2. Посмотрите вокруг себя и найдите в форме окружающих предметов простые геометрические тела.

7.2. Общие сведения о проецировании. Изображения предметов на чертежах в соответствии с правилами государственного стандарта выполняют по способу (методу) прямоугольного проецирования. Проецированием будем называть процесс получения проекций предмета.

Рассмотрим пример. Возьмем в пространстве произвольную точку А и какую-нибудь плоскость. Обозначим эту плоскость, например, прописной буквой П (пи) греческого алфавита с индексом один - т. е. П₁ (рис. 24). Проведем через точку А прямую так, чтобы она пересекла плоскость П₁ в некоторой точке А'. Тогда точка А' будет проекцией точки А. Проекции точек будем обозначать теми же буквами, что и сами точки, но со штрихом. Плоскость, на которой получается проекция, называется плоскостью проекций. Прямая АА' называется проецирующим лучом. С его помощью точка А проецируется на плоскость П₁.

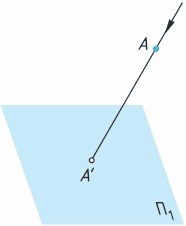
Рис. 24

Примечание. Существуют и другие обозначения проекций точек — A₁, A₂, А₃ — и плоскостей проекций — Н, V, W.

Указанным способом могут быть построены проекции всех точек любой фигуры. Так, чтобы получить проекцию А'B' отрезка АВ прямой (рис. 25, а), необходимо провести проецирующие лучи через две точки отрезка - А и В. При этом, если прямая или ее отрезок совпадают по направлению с проецирующим лучом (отрезок CD на рис. 25, б), они проецируются на плоскость проекций в точку. На изображениях проекции совпадающих точек обозначают знаком =, например: C = D', как на рисунке 25, б.

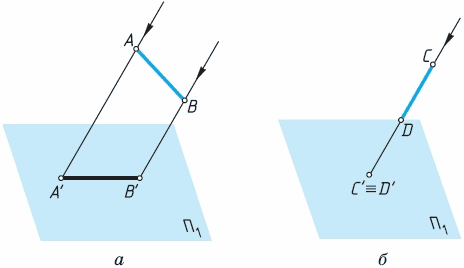
Рис. 25

Для построения проекции какой-либо фигуры необходимо через ее точки провести воображаемые проецирующие лучи до пересечения их с плоскостью проекций. Проекции всех точек фигуры на плоскости и образуют проекцию заданной фигуры.

Рассмотрим, например, получение проекции такой геометрической фигуры, как треугольник (рис. 26).

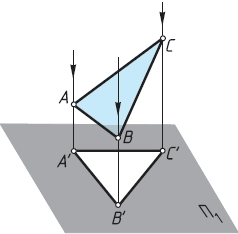
Рис. 26

Проекцией точки А на заданную плоскость П₁ будет точка А' как результат пересечения проецирующего луча АА' с плоскостью проекций. Проекциями точек Б и С будут точки В' и С. Соединив на плоскости точки А', В' и С отрезками прямых, получим фигуру А'В'С, которая и будет проекцией заданной фигуры.

В дальнейшем под термином проекция мы будем понимать изображение предмета на плоскости проекций.

Слово «проекция» латинское. В переводе оно означает «бросать (отбрасывать) вперед».

Положите на бумагу какой-нибудь плоский предмет и обведите его карандашом. Вы получите изображение, соответствующее проекции этого предмета. Примерами проекций являются фотографические снимки, кинокадры и др.

Изображения предметов, полученные путем проецирования, будем называть проекционными.

1. Что представляет собой проецирование?
2. Как строить на плоскости проекцию точки? проекцию фигуры?

7.3. Центральное и параллельное проецирование. Если проецирующие лучи, с помощью которых строится проекция предмета, исходят из одной точки, проецирование называется центральным (рис. 27). Точка, из которой исходят лучи, называетсяцентром проецирования. Полученная при этом проекция называется центральной.

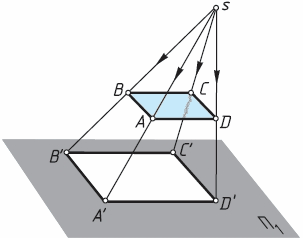
Рис. 27

Центральную проекцию часто называют перспективной. Примерами центральной проекции являются фотоснимки и кинокадры, тени, отброшенные от предмета лучами электрической лампочки, и др. Центральные проекции применяют в рисовании с натуры.

Если проецирующие лучи параллельны друг другу (рис. 28), то проецирование называется параллельным, а полученная проекция - параллельной. Параллельной проекцией можно условно считать солнечные тени предметов. Примеры параллельного проецирования приведены на рисунках 25, а и 26.

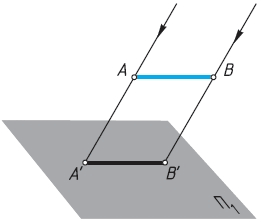
Рис. 28

Строить изображение предмета при параллельном проецировании проще, чем при центральном. Так, если отрезок АВ (рис. 28) или любая плоская фигура, как, например, на рисунке 29, параллельны плоскости проекций, то их проекции и сами проецируемые фигуры равны.

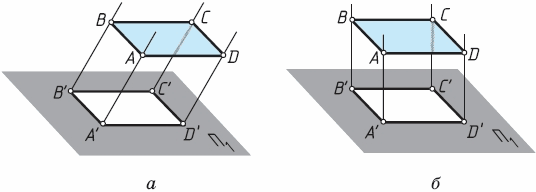
Рис. 29

При параллельном проецировании все лучи падают на плоскость проекций под одинаковым углом. Если это любой угол, который не равен 90°, как на рисунке 29, а или на рисунке 25, а, то проецирование называется косоугольным.

В том случае, когда проецирующие лучи перпендикулярны плоскости проекций (см. рис. 29, б), т. е. составляют с ней угол 90°, проецирование называется прямоугольным (см. рис. 26). Полученная при этом проекция называется прямоугольной.

1. Какое проецирование называется центральным? параллельным? косоугольным? прямоугольным?
2. Почему строить изображение в параллельной проекции проще, чем в центральной?

Призмы, пирамидыМетод проекций. Виды проецирования.

Начертательная геометрия является одним из разделов геометрии, в котором пространст
венные объекты с их геометрическими закономерностями изучаются в виде изображений на
плоскости. Начертательная геометрия также рассматривает способы решения пространст
венных задач посредством геометрических построений на плоскости. Способ изображения объ
емного предмета на плоскости называют проецированием, само изображение – проекцией, а
плоскость, на которой его изобразили – плоскостью проекций.
«П р о е к ц и я » – латинское слово, в переводе на русский язык оно означает «отбрасывать
вперёд».
П р о е к ц и е й называется изображение объёмного предмета на плоскости.
П р о е ц и р о в а н и е м называется процесс построения изображения предмета на плоскости.
П л о с к о с т ь ю п р о е к ц и й называется плоскость, на которую предмет проецируют.

Примером проекции можно назвать тень, отбрасываемую геометрической фигурой на поверх
ность. Например, если направить на геометрическую фигуру луч света из одной точки, то на
отстоящей от этой фигуры плоскости получится её тень.
В данном случае луч света был направлен из одной точки. Эта точка называется центром про
ецирования, а проекция, соответственно, называется центральной.
Центральную проекцию также часто называют перспективной. Её применяют при рисовании,
наглядном изображении массивных предметов, зданий и сооружений. По принципу центрального
проецирования выполняется изображения на фотографиях, в кинофильмах. По этому же принци
пу устроен и орган зрения человека – глаз.
Если проецирующие лучи параллельны друг другу, то процесс проецирования называется парал
лельным, а полученное изображение – параллельной проекцией. Примером такого проецирования
можно условно считать солнечные тени предметов.
При параллельном проецировании все лучи падают на плоскость проекций под одним и тем же
углом. Если лучи падают не под прямым углом, то проецирование называют косоугольным. Если
под прямым – то прямоугольным.
В косоугольной проекции, как и в центральной, форма и величина предмета искажаются.
В практике черчения чаще всего используют такой способ построения графических изображе
ний, при котором предмет и его проекция не искажаются. Для этого необходимо, чтобы проеци
рующие лучи были параллельны между собой, чтобы все они были перпендикулярны к плоскости
проекций и чтобы геометрическая фигура также была расположена параллельно плоскости про
екций. Этот способ называется – прямоугольным параллельным проецированием
При прямоугольном параллельном проецировании проецирующие лучи
а) параллельны между собой,
б) все они были перпендикулярны к плоскости проекций.
Свойства проецирования:
1. Точка проецируется точкой. Прямая – прямой.
2. Любая точка или линия в пространстве имеет единственную проекцию.
3. Для построения проекции прямой достаточно построить проекции двух её точек.
4. Если прямая совпадает с направлением проецирования, она проецируется в точку.
5. Каждая точка на плоскости проекций может являться проекцией множества точек.
6. Каждая линия на плоскости проекций может являться проекцией множества линий.
7. Если точка принадлежит прямой, то её проекция принадлежит проекции этой прямой.
Давайте договоримся о том, как мы будем обозначать точки и отрезки в пространстве, и как
будем обозначать их проекции:
Точка в пространстве обозначается затушеванным кругом диаметром приблизительно 1 – 2 мм и
прописной (заглавной) буквой латинского алфавита.
Проекция точки обозначается незатушеванной окружностью того же размера и той же буквой латин
ского алфавита, но строчного (маленькие) начертания.
Отрезки соответственно будут обозначаться AB, а их проекции ab.
Плоскости будем обозначать прописной (заглавной) буквой греческого алфавита.
Углы обозначать строчной (маленькой) буквой греческого алфавита.
Дополнительно: аксонометрические проекции, перспектива.