Поделиться
Опеделение реакций в опорах балочных систем .docx
Министерство образования и науки Краснодарского края
Государственное бюджетное профессиональное образовательное учреждение
Краснодарского края
«Армавирский механико – технологический техникум»
Методическое пособие
для проведения
практического занятия
на тему:
«ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОПОРАХ БАЛОЧНЫХ СИСТЕМ ПОД ДЕЙСТВИЕМ СОСРЕДОТОЧЕННЫХ СИЛ И ПАР СИЛ»
по дисциплине: «Техническая механика»
для студентов 2 курса
спец. 15.02.05
Разработал преподаватель: Е.В. Игнатова
|
|
|
2016
1 ЦЕЛЬ РАБОТЫ
Знать:
- знать три формы уравнений равновесия и уметь их использовать при определении реакций в опорах балочных систем;
Уметь:
- выполнять проверку правильности решения.
2 ДЛЯ ЗАЧЕТА РАБОТЫ НЕОБХОДИМО:
- изучить теоретический материал с помощью методического пособия;
- по варианту задания выполнить расчеты по определению величин реакций в опоре защемленной балки
- провести проверку правильности решения;
- ответить на контрольные вопросы.
3 КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА
3.1 Разновидности опор балочных систем
Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами.
Высота сечения балки незначительна по сравнению с длиной.
Жесткая заделка (защемление) (чертеж 1)
Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы RАx и RАy и парой с моментом MR.
Для определения этих неизвестных удобно использовать систему
уравнений виде 
Каждое уравнение имеет одну неизвестную
величину и решается без подстановок.
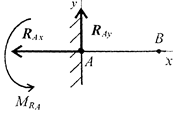
Чертеж 1
Для контроля правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например В:
Шарнирно-подвижная опора (чертеж 2)
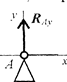
Чертеж 2
Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.
Шарнирно-неподвижная опора (чертеж 3)
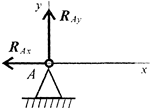
Чертеж 3
Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
3.2 Три формы уравнений равновесия
Теоретически уравнений можно записать бесконечное множество, но практически доказано, что на плоскости можно составить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии.
Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.
Для разных случаев используются три группы уравнений равновесия.
Первая форма уравнений равновесия:
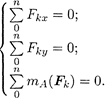
Вторая форма уравнений равновесия:
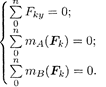
Третья форма уравнений равновесия:
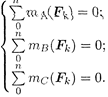
4 ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
Одноопорная (защемленная) балка нагружена сосредоточенными силами и парой сил (чертеж 4) Определить реакции заделки.
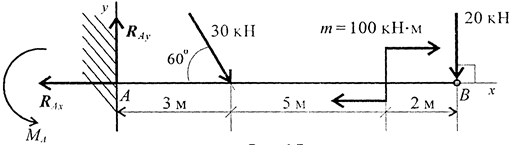
Чертеж 4
Решение:
1.В заделке может возникнуть реакция, представляемая двумя составляющими (RАx и RАy), и реактивный момент МА. Нанести на схему балки возможные направления реакций.
Замечание. Если направления выбраны неверно, при расчетах получим отрицательные значения реакций. В этом случае реакции на схеме следует направить в противоположную сторону, не повторяя расчета.
В силу малой высоты считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке. Для решения удобно использовать систему уравнений равновесия в первой форме. Каждое уравнение будет содержать одну неизвестную.
2. Используют систему уравнений:
Знаки полученных реакций (+), следовательно, направления реакций выбраны верно.
3. Для проверки правильности решения составить уравнение моментов относительно точки В.
ткВ
= -МА + RAy • 10 - 30 • 7 • sin 60° +100
= 0.
Подставить значения полученных реакций:
-377,94 + 45,98 • 10 - 210 • 0,866 + 100 = 0;
-559,8 + 559,8 = 0.
Решение выполнено верно.
5 ЗАДАНИЕ
Определить величины реакций в опоре защемленной балки. Провести проверку правильности решения.
Рисунок 1
Рисунок 2
Рисунок 3
ВАРИАНТЫ ЗАДАНИЙ
|
Вариант |
Рисунок |
F1, кH |
F2, кH |
m, кНм |
a, м |
|
1 |
3 |
10 |
4,4 |
14 |
0,2 |
|
2 |
2 |
12 |
4,5 |
13 |
0,2 |
|
3 |
1 |
14 |
4,6 |
14 |
0,3 |
|
4 |
3 |
16 |
4,8 |
15 |
0,3 |
|
5 |
2 |
18 |
3,2 |
12 |
0,4 |
|
6 |
1 |
20 |
7,5 |
11 |
0,4 |
|
7 |
3 |
22 |
8,2 |
10 |
0,5 |
|
8 |
2 |
24 |
16 |
9 |
0,5 |
|
9 |
1 |
26 |
12,8 |
8 |
0,6 |
|
10 |
3 |
25 |
14 |
7 |
0,6 |
|
11 |
2 |
28 |
17,3 |
6 |
0,7 |
|
12 |
1 |
11 |
21,1 |
5 |
0,7 |
|
13 |
3 |
13 |
15 |
13 |
0,8 |
|
14 |
2 |
15 |
5,8 |
15 |
0,8 |
|
15 |
1 |
17 |
6,3 |
4 |
0,9 |
|
16 |
3 |
19 |
11,2 |
2 |
0,9 |
|
17 |
2 |
21 |
14,5 |
8 |
0,2 |
|
18 |
1 |
23 |
13 |
3 |
0,2 |
|
19 |
2 |
25 |
17 |
12 |
0,3 |
|
20 |
3 |
29 |
13,2 |
14 |
0,3 |
|
21 |
2 |
30 |
14 |
5 |
0,4 |
|
22 |
1 |
9 |
3,5 |
6 |
0,4 |
|
23 |
3 |
10 |
18 |
7 |
0,5 |
|
24 |
2 |
12 |
5,5 |
8 |
0,5 |
|
25 |
1 |
14 |
21 |
9 |
0,6 |
|
26 |
3 |
16 |
11 |
10 |
0,6 |
|
27 |
2 |
18 |
4,5 |
11 |
0,7 |
|
28 |
1 |
20 |
5,6 |
12 |
0,7 |
|
29 |
3 |
22 |
6,1 |
13 |
0,8 |
|
30 |
2 |
24 |
10 |
14 |
0,8 |
6 КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое балка?
2. Перечислить разновидности опор балочных систем?
3. Какую из форм уравнения равновесия целесообразно использовать при определении реакции в заделке?
4. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?
5. Указать единицу измерения момента.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
