Практическая работа специальности 15.02.05. «Техническая эксплуатация оборудования в торговле и общественном питании»

Министерство образования и науки Краснодарского края

Государственное бюджетное профессиональное образовательное учреждение

Краснодарского края

«Армавирский механико – технологический техникум»

Методическое  пособие

для проведения

практического занятия   

на тему:

«ОПРЕДЕЛЕНИЕ РАВНОДЕЙСТВУЮЩЕЙ ПЛОСКОЙ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ № »  

по дисциплине: «Техническая механика»

для студентов 2 курса 

спец. 15.02.01, 15.02.05, 19.02.03, 19.02.06, 19.02.08

Разработал преподаватель: Е.В. Игнатова

2019

1 ЦЕЛЬ РАБОТЫ

Знать:

- способы сложения двух сил и разложение силы на составляющие;

- геометрический и аналитический способы определения равнодействующей силы;

- условия равновесия плоской сходящейся системы сил.

Уметь:

- определять равнодействующую системы сил;

- решать задачи на равновесие аналитическим способом, рационально выбирая координатные оси.

2 ДЛЯ ЗАЧЕТА РАБОТЫ НЕОБХОДИМО:

- изучить теоретический материал с помощью  методического пособия;

- по варианту задания выполнить расчеты  по определению равнодействующей плоской системы сходящихся сил;

- ответить на контрольные вопросы.

3 КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

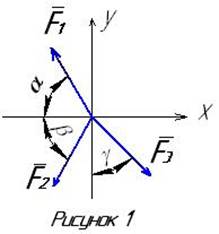
         Система сил, линия действия которых пересекаются в одной точке, называется сходящейся (чертеж 1).

Чертеж 1

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось от начала и конца вектора.(чертеж 2)

F_x=Fcosα

Чертеж 2

         Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Проекция F_x имеет знак положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси

Расчетные формулы

Равнодействующая системы сил определяется по формуле

R=,

где  - проекции равнодействующей на оси координат

где  R_nx , R_ny  -  проекции векторов-сил системы на оси координат

,

где - угол равнодействующей с осью ОX

,

где - угол равнодействующей с осью ОY

Условие равновесия

         Если плоская система сходящихся сил находится в равновесии, многоугольник сил должен быть замкнут.

4 ПОРЯДОК  ВЫПОЛНЕНИЯ  РАБОТЫ

1. Изобразить заданную систему сил F₁, F₂, F₃ в системе координат xy и показать числовые значения углов, а также указать числовые значения сил.
2. Составить векторное равенство для равнодействующей

R= F₁+ F₂+ F₃

3.     Спроецировать это равенство на оси координат

R_х= F_1х+ F_2х+ F_3х

R_y= F_1y+ F_2y+ F_3y

4. Вычислить величину равнодействующей по формуле

R=

5. Определить направляющие косинусы равнодействующей по формулам

5 ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ

Дано: рисунок 1

F₁=30кН                α=150˚

F₂=20кН                β=45˚

F₃=10кН                γ=210˚

Решение:

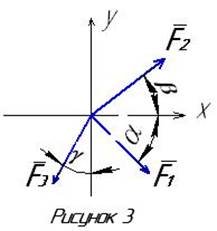
1.      Изобразить заданную систему сил F₁, F₂, F₃ в системе координат xy

Чертеж 3

2.     Составить векторное равенство для равнодействующей

R= F₁+ F₂+ F₃

3.     Спроектировать  равенство на оси координат

R_х= F_1х+ F_2х+ F_3х

R_y= F_1y+ F_2y+ F_3y

Произвести вычисления

R_х= F₁ cos30˚ - F₂ cos45˚- F₃ cos60˚

R_х=

R_y== F₁ cos60˚ - F₂ cos45˚+ F₃ cos30˚

R_y=

4.     Вычислить величину равнодействующей

R=

R=

5.     Вычислить направляющие косинусы равнодействующей

6  ВАРИАНТЫ ЗАДАНИЙ

7 КОНТРОЛЬНЫЕ    ВОПРОСЫ

1.     Дать определение проекции силы на ось.

2.     Дать определение равнодействующей.

3.     Аналитическое определение равнодействующей плоской сходя­щейся системы сил.

4.     Геометрическое определение равнодействующей плоской сходя­щейся системы сил.

5.     Формула для определения направляющих косинусов силы.