
Министерство образования, науки и молодежной политики Краснодарского края
Государственное бюджетное профессиональное образовательное учреждение
Краснодарского края
«Армавирский механико – технологический техникум»
Методическое пособие
для проведения
практического занятия №2
на тему:
«ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ»
по дисциплине: «Техническая механика»
для студентов 2 курса
спец. 15.02.01, 15.02.05, 19.02.03, 19.02.06, 19.02.08
Разработал преподаватель: Е.В. Игнатова
|
|
|
2021
1 ЦЕЛЬ РАБОТЫ
Знать:
- три формы уравнений равновесия и уметь ими пользоваться при определении реакций в опорах балочных систем.
Уметь:
- приводить произвольную плоскую систему сил к точке.
2 ДЛЯ ЗАЧЕТА РАБОТЫ НЕОБХОДИМО:
- изучить теоретический материал с помощью методического пособия;
- по варианту задания выполнить расчеты по определению величин реакций для балки с шарнирными опорами;
- провести проверку правильности решения;
- ответить на контрольные вопросы.
3 КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА
3.1 Момент силы относительно точки
Сила, не проходящая через точку крепления тела, вызывает вращение тела относительно точки, поэтому действие такой силы на тело оценивается моментом.
Момент силы относительно точки численно равен произведению модуля силы на расстояние от точки до линий действия силы. Перпендикуляр, опущенный из точки на линию действия силы (Чертеж 1), называется плечом силы.
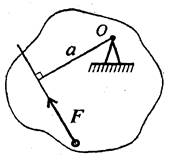
Чертеж 1
Обозначение момента Мо(F)
Мо(F) = F a
Единица измерения Мо(F) = Н м.
Момент считается положительным, если сила разворачивает тело по часовой стрелке.
Момент силы относительно точки равен нулю, если линия действия силы проходит через точку, т. к. в этом случае расстояние от точки до силы равно нулю.
3.2 Условие равновесия произвольной плоской системы сил
Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил системы на любую ось равнялась нулю и алгебраическая сумма моментов всех сил системы относительно любой точки в плоскости действия сил равнялась нулю.
Первая форма уравнений равновесия:
1. ![]() ;
;
![]() ;
;
![]()
Проверка: ![]()
Вторая форма уравнений равновесия:
2. ![]() ;
;
![]() ;
;
![]()
Проверка: ![]()
4 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
4.1 Освободить балку от связей, заменив их реакциями связей RA, RB.
Замечание. Если направления выбраны неверно, при расчетах получим отрицательные значения реакций. В этом случае реакции на схеме следует направить в противоположную сторону, не повторяя расчета.
В силу малой высоты считают, что все точки балки находятся на одной прямой; две неизвестные реакции приложены в одной точке. Для решения удобно использовать систему уравнений равновесия в первой форме. Каждое уравнение будет содержать одну неизвестную.
4.2 Использовать систему уравнений:
![]() ;
;
![]() ;
;
![]()
Знаки полученных реакций (+), следовательно, направления реакций выбраны, верно.
4.3 Для проверки правильности решения составить уравнение моментов относительно точки В.
![]()
4.4 Подставить значения полученных реакций. Если ответ равен нулю, то решение выполнено, верно.
5 ЗАДАНИЕ
Определить реакции шарнирно-подвижной и шарнирно-неподвижной опор балки, нагруженной силой F парой с моментом М. Весом балки пренебречь. Провести проверку правильности решения.
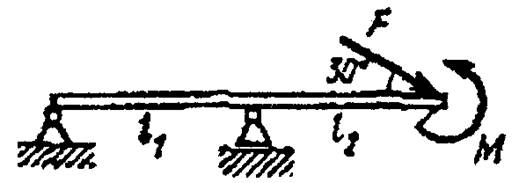
Рисунок 1
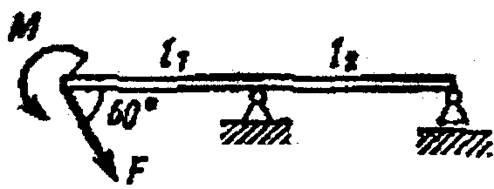
Рисунок 2

Рисунок 3
ВАРИАНТЫ ЗАДАНИЙ
|
Вариант |
Рисунок |
F , кН |
М, кНм |
l1, м |
l2, м |
|
1 |
1 |
13 |
9 |
0,3 |
0,9 |
|
2 |
1 |
10 |
8 |
0,4 |
1,4 |
|
3 |
1 |
5 |
7 |
0,7 |
1,1 |
|
4 |
1 |
8 |
6 |
0,8 |
0,4 |
|
5 |
1 |
3 |
9 |
0,5 |
0,7 |
|
6 |
1 |
7 |
11 |
0,7 |
0,5 |
|
7 |
1 |
4 |
12 |
0,4 |
0,8 |
|
8 |
1 |
11 |
13 |
0,5 |
0,5 |
|
9 |
1 |
6 |
12 |
1,2 |
0,6 |
|
10 |
1 |
9 |
15 |
0,9 |
0,3 |
|
11 |
2 |
10 |
16 |
1,0 |
0,4 |
|
12 |
2 |
7 |
13 |
1,3 |
0,7 |
|
13 |
2 |
6 |
8 |
0,8 |
1,2 |
|
14 |
2 |
11 |
9 |
0,5 |
1,4 |
|
15 |
2 |
14 |
10 |
0,4 |
1,0 |
|
16 |
2 |
5 |
7 |
0,7 |
0,9 |
|
17 |
2 |
12 |
14 |
0,6 |
0,6 |
|
18 |
2 |
5 |
13 |
0,8 |
0,6 |
|
19 |
2 |
8 |
12 |
0,5 |
0,9 |
|
20 |
2 |
13 |
9 |
0,4 |
0,6 |
|
21 |
3 |
4 |
10 |
0,6 |
0,7 |
|
22 |
3 |
8 |
14 |
0,8 |
0,2 |
|
23 |
3 |
5 |
10 |
0,2 |
0,5 |
|
24 |
3 |
4 |
6 |
0,6 |
0,1 |
|
25 |
3 |
9 |
7 |
0,3 |
0,4 |
|
26 |
3 |
12 |
8 |
0,2 |
0,8 |
|
27 |
3 |
3 |
5 |
0,5 |
0,7 |
|
28 |
3 |
10 |
12 |
0,4 |
0,4 |
|
29 |
3 |
3 |
11 |
0,3 |
0,7 |
|
30 |
3 |
6 |
10 |
0,6 |
0,4 |
6 КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки?
2. Какие виды опор вам известны?
3. Как определить момент силы относительно точки?
4. Указать единицу измерения момента.
5. Что называется балкой?
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.