Практическая работа специальности 15.02.05. «Техническая эксплуатация оборудования в торговле и общественном питании»

Министерство образования и науки Краснодарского края

Государственное бюджетное профессиональное образовательное учреждение

Краснодарского края

«Армавирский механико – технологический техникум»

Методическое пособие

для проведения

практического занятия

на тему:

«РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ АНАЛИТИЧЕСКИМ СПОСОБОМ»

по дисциплине: «Техническая механика»

для студентов 2 курса

15.02.05

Разработал преподаватель: Е.В. Игнатова

2016

1 ЦЕЛЬ РАБОТЫ

Знать:

- условия равновесия плоской сходящейся системы сил, аналитический способ определения равнодействующей силы;

Уметь:

-определять равнодействующую системы сил, решать задачи на равновесие аналитическим способом, рационально выбирая координатные оси.

2 ДЛЯ ЗАЧЕТА РАБОТЫ НЕОБХОДИМО:

- изучить теоретический материал с помощью  методического пособия;

- по варианту задания выполнить расчеты по определению системы сил аналитическим способом;

- ответить на контрольные вопросы.

3 КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

3.1 Проекция силы на ось

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (чертеж 1).

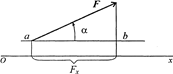
Чертеж 1

F_x = Fcosα

Величина проекции силы на ось равна произведению модуля си­лы на косинус угла между вектором силы и положительным напра­влением оси.

Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (чертеж 2).

Чертеж 2

F_1x = F₁ cosα₁ > 0;    F_2x = F₂ cosα₂ = -F₂ cos β₂

F_3x = F₃ cos90° =0;    F_4x = F₄ cos 180° = -F₄.

Проекция силы на две взаимно перпендикулярные оси (чертеж 3)

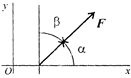
Чертеж 3

F_x = Fcosα > 0;  F_y = F cosβ = Fsinα > 0.

3.2 Условия равновесия плоской системы сходящихся сил в аналитической форме

Плоская система сходящихся сил находится в равновесии, ес­ли алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской сходящейся системы сил:

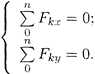
В задачах координатные оси выбирают так, чтобы решение бы­ло наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.

4 ПРИМЕР  ВЫПОЛНЕНИЯ  ЗАДАНИЯ

Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях (чертеж 4).

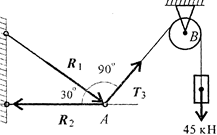
Чертеж 4

Решение:

1. Нанести на схему возможные направления усилий, приложен­ных в точке А. Реакции стержней — вдоль стержней, усилие от каната -— вдоль каната от точки А к точке В.

2. Груз находится в равновесии, следовательно, в равновесии находится точка А в которой пересекаются три силы.

Освободить точку А от связей и рассмотреть ее равновесие (чертеж 5).

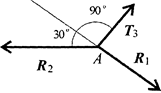
Чертеж 5

3амечание. Рассмотреть только силы, приложенные к точке А. Груз растягивает канат силой 45 кН по всей длине, поэтому усилие от каната известно:

Т₃ = 45 кН.

2. Записать условия равновесия плоской системы сходящихся сил в аналитической форме

∑ F_ку=Т₃ – R₂ cos60°

R₂ = Т₃/ cos60°

R₂ =45/0,5=90кН

∑ F_кх=R₁ – R₂ cos30°

R₁ =R₂ cos30°

R₁=90•0,866=77,94кН

Ответ: усилия в стержнях R₁ =77,94кН;  R₂ =90кН

5 ЗАДАНИЕ

Определить силы, нагружающие стержни кронштейна. Кронштейн удерживает в равновесии грузы F₁ и F₂ или груз F₁ и растянутую пружину, сила упругости которой F₂. Весом частей конструкции, а также трением на блоке пренебречь.

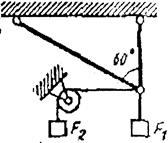
Рисунок 1

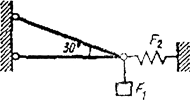
Рисунок 2

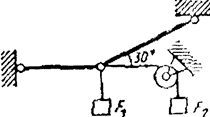
Рисунок 3

Рисунок 4

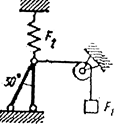
Рисунок 5

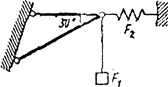
Рисунок 6

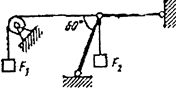
Рисунок 7

ВАРИАНТЫ  ЗАДАНИЙ

6 КОНТРОЛЬНЫЕ    ВОПРОСЫ

1.     Чему равна проекция силы на ось ОХ?

2.     Чему равна проекция силы на ось ОУ?

3.     Когда проекция имеет положительный знак?

4.     Когда проекция имеет отрицательный знак?

5.     Какое условие равновесия плоской системы сходящихся сил в аналитической форме?