Практическая работа специальности 38.02.04.

Практическое занятие № 5

Тема: Исследование функции с помощью производной и построение графика

Цель занятия: приобретение практического навыка исследования функции с помощью производной и построения графика

Наглядные пособия: учебники, таблица производных

Литература:

1.   Григорьев С.Г. Математика: учебник для СПО. – М.: Изд. центр «Академия», 2014.

2.   Гусев В.А. Математика для профессий и специальностей соц.-экон. профиля: учебник для образовательных учреж. нач. и сред. проф. образ. – М.: Изд. центр «Академия», 2013.

Теоретические сведения

Общая схема исследования функции и построения графика функции

Исследование функции целесообразно вести в определенной последовательности.

1. Найти область определения функции.

2. Найти (если это можно) точки пересечения графика с осями координат.

3. Найти интервалы знакопостоянства функции (промежутки, на которых >0 или <0).

4. Выяснить, является ли функция четной, нечетной или общего вида.

5. Найти интервалы монотонности функции.

6. Найти экстремумы функции.

7. Найти интервалы выпуклости и точки перегиба графика функции.

Пример. Исследовать функцию  и построить ее график.

Решение:

1.

2.

Точка (0;0) – точка пересечения графика с осями Ох и Оу.

3. Функция знакоположительна (у>0) в интервалах  и , знакоотрицательна – в  и

4. Функция   является нечетной т.к. . Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при .

5..

Так как у’>0 в области определения, то функции является возрастающей на каждом интервале области определения.

6. Т.к. , то критическими точками является точки

 х₁ = –1 и х₂ = 1.

Данные точки не принадлежат области определения функции, значит, функция экстремумов не имеет.

7. Найдем у”

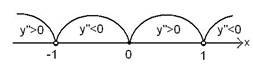
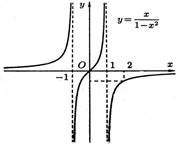Точка (0;0) – точка перегиба графика функции.

График выпуклый вверх на интервалах  и ; выпуклый вниз на интервалах  и

Практическая часть

Вариант 1

1.      Найдите производную функции:

a.      f(x) = 2

b.    f(x) = (

c.   f(x) =

d.    f(x) =

2.           Найдите критические точки функции: а)
б).

3.   Найдите точки экстремума функции:

4.  Найдите промежутки возрастания и убывания функции:  

5.  Исследуйте функцию и постройте её график:.

Вариант 2

1.      Найдите производную функции:

a.      f(x) = 3

b.    f(x) = (

c.  

d.    f(x) =

2.  Найдите критические точки функции: а) 
б) .

3.  Найдите точки экстремума функции:

4.  Найдите промежутки возрастания и убывания функции:

5.  Исследуйте функцию и постройте её график:

Контрольные вопросы:

1.      Как найти критические точки функции?

2.      Как найти интервалы монотонности функции?

3.      Как найти точки экстремумов функции?

4.      Как найти интервалы выпуклости и точки перегиба функции?

5.