Практическая работа специальности 38.02.04.

Практическое занятие № 6

Тема: Нахождение неопределенных и определенных интегралов.

Цель занятия: повторить, обобщить и систематизировать знания по нахождению неопределенных и определенных интегралов

Наглядные пособия: учебники, таблица интегралов

Литература:

1.                       Григорьев С.Г. Математика: учебник для СПО. – М.: Изд. центр «Академия», 2019.

2.                       Гусев В.А. Математика для профессий и специальностей соц.-экон. профиля: учебник для образовательных учреж. нач. и сред. проф. образ. – М.: Изд. центр «Академия», 2013.

Теоретические сведения

Неопределенным интегралом от функции  называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:  где

Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:

Для проверки правильности выполненного интегрирования необходимо продифференцировать результат интегрирования и сравнить полученную функцию с подынтегральной.

Каждая из приведенных в таблице формул справедлива на промежутке, не содержащем точек разрыва подынтегральной функции. Вычисление интегралов с использованием таблицы и основных свойств называют непосредственным интегрированием.

Пример. Пользуясь таблицей основных интегралов и свойствами неопределенного интеграла, найти интегралы:

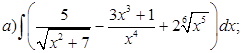
Решение.

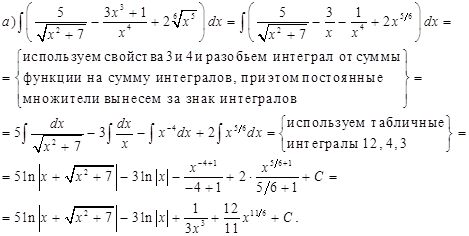
Метод замены переменной

Теорема 1. Пусть монотонная, непрерывно дифференцируемая функция, тогда

                        (1)

При этом, если  то  где — функция, обратная .

Формула (1) называется формулой замены переменной в неопределенном интеграле.

Алгоритм замены переменной:

1) Связать старую переменную интегрирования  с новой переменной  с помощью замены .

2) Найти связь между дифференциалами .

3) Перейти под знаком интеграла к новой переменной.

4) Проинтегрировать и в полученной первообразной вернуться к старой переменной, подставив

Пример. Проинтегрировать подходящей заменой переменной.

Решение:

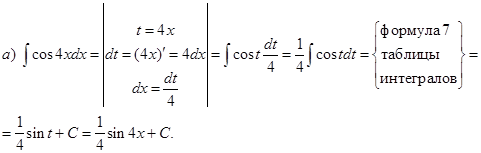
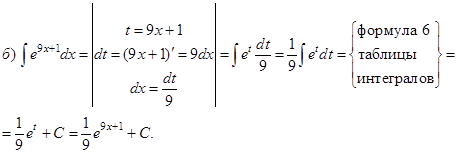
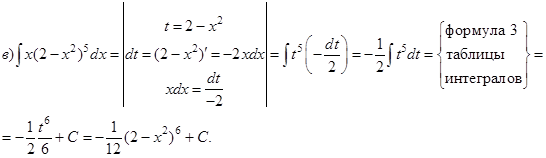
Определенный интеграл от функции, непрерывной на отрезке , вычисляется по формул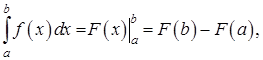е:  где — первообразная для функции , т. е. Формула называется формулой Ньютона — Лейбница.

Свойства определенного интеграла:

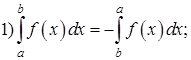
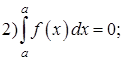
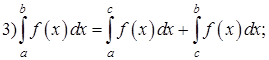
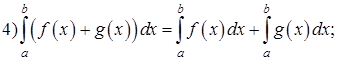
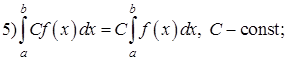
6) Если  для всех , то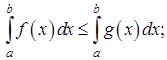

7) Если  для всех , то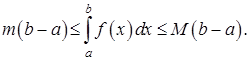

При вычислении определенного интеграла для нахождения первообразной используют те же методы, что и для нахождения неопределенного интеграла, т. е. замену переменной, интегрирование по частям и т. д. Однако есть ряд особенностей. При замене переменной по формуле (1) необходимо в соответствии с заменой менять пределы интегрирования: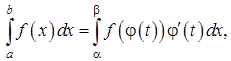        

где  — обратная к  функция.

Формула интегрирования по частям приобретает вид: 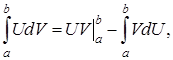Пример. Вычислить определенный интеграл

Решение.

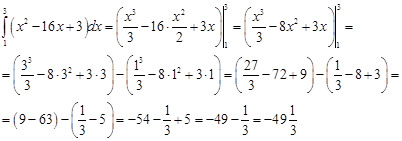
Практическая часть

Контрольные вопросы:

1.      Что называется неопределенным интегралом?

2.      Сформулируйте алгоритм нахождения неопределенного интеграла методом замены переменной?

3.      Запишите формулу интегрирования по частям.

4.      Сформулируйте понятие  определенного интеграла.

5.      Формула Ньютона — Лейбница.

6.