Практическая работа специальности 38.02.04.

Практическое занятие № 7

Тема: Вычисление площадей плоских фигур, объемов тел вращения, пути пройденного точкой.

Цель занятия: приобретение практического навыка в вычислении площадей плоских фигур, объемов тел вращения, пути, пройденного точкой

Наглядные пособия: учебники, таблица интегралов

Литература:

1.     Григорьев С.Г. Математика: учебник для СПО. – М.: Изд. центр «Академия», 2014.

2.       Гусев В.А. Математика для профессий и специальностей соц.-экон. профиля: учебник для образовательных учреж. нач. и сред. проф. образ. – М.: Изд. центр «Академия», 2013.

Теоретические сведения

1.     Криволинейная трапеция

Пусть на отрезке [а; b] оси Ох задана непрерывная функция f, не меняющая на нем знака. Фигуру, ограниченную графиком этой функции, отрезком [а; b] и прямыми х = а и х = b (рис. 1), называют криволинейной трапецией.

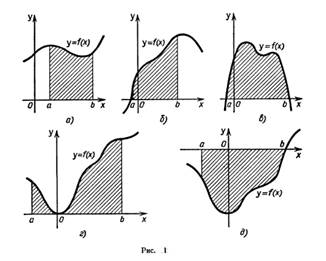
2.     Площадь криволинейной трапеции.

S=F(b)-F(a).

Алгоритм нахождения площади криволинейной трапеции

1.     Построить графики линий.

2.     Определить криволинейную трапецию.

3.     Выделить функцию  f , ограничивающую трапецию.

4.     Определить отрезок [a; b] оси Ох.

5.     Найти одну из первообразных функции  f .

6.     Используя формулу   S=F(b)-F(a) , вычислить площадь.   

Пример: Вычислить площадь криволинейной трапеции, ограниченной линиями
у = 4 - х² и у = 0

Решение:   1. Построим криволинейную трапецию:  у = 4 - х²- квадратичная функция, график – парабола, ветви направлены вниз.
у = 0 - ось абсцисс.

2. Найдём [а;b]: 4-х² = 0;    х² = 4;     х = -2 или х = 2, т. е. а = -2 b = 2

3. Найдём площадь криволинейной трапеции по формуле: S = F(b) – F(а)

3.      Вычисление пути, пройденного точкой

Путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью за промежуток времени от до вычисляется по формуле .

Пример: Скорость движения точки  м/с. Найти путь, пройденный точкой за 4-ю секунду.

Решение: Согласно условию, . Следовательно,

Пример: Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью м/с, второе  со скоростью v = (4t+5) м/с. На каком расстоянии друг от друга они окажутся через 5 с?

Решение: очевидно, что искомая величина есть разность расстояний, пройденных первым и вторым телом за 5 с:

Пример: Тело брошено с поверхности земли вертикально вверх со скоростью и = (39,2—9,8^) м/с. Найти наибольшую высоту подъема тела.

Решение: тело достигнет наибольшей высоты подъема в такой момент времени t, когда v = 0, т.е. 39,2—9,8t = 0, откуда I = 4 с. По формуле (1) на ходим

Практическая часть

Вариант 1

1.     Вычислите определенный интеграл:

а) 

2. Скорость точки, движущейся прямолинейно, задана уравнением v=3t²­2t­1,м/c. Вычислить путь, пройденный точкой за 5 секунд после начала движения.

3. Найдите площадь заштрихованной фигуры:

                              y                                        

                       1          y=

                                                   х

       - π           -              0                

                                -1

4.Найти площадь фигуры, ограниченной кривыми, заданными уравнениями:

          а)  y=2x­x²;         y=0.

б) ;

Вариант 2

1.     Вычислите определенный интеграл

а)        

2.     Скорость точки, движущейся прямолинейно, задана уравнением v=6t²-4t-10,см/с. Вычислить  путь, пройденный точкой за 4с от начала движения.

3.     Найдите площадь заштрихованной фигуры:

                y                                        

          1                   y=

                                                   х

        -              0                     π        

         -1

4.Найти площадь фигуры, ограниченный кривыми, заданными уравнениями:

      а)   y= x²,     y= ­3x.      

  б).

Контрольные вопросы:

1.     Что называется определенным интегралом?

2.     Как вычисляется определенный интеграл?

3.     Свойства определенного интеграла?

4.     Что называется криволинейной трапецией?

5.     Как с помощью интеграла найти площадь криволинейной трапеции; путь, пройденный телом при неравномерном движении.