Практическая работа

Задача поиска кратчайшего пути

Цель работы – решение задачи нахождения кратчайшего пути в графе средствами Excel.

Порядок выполнения работы Рассмотрим задачу: определить наикратчайший путь между

вершиной 1 и вершиной 7 на графе, представленном на рис. 2.1.

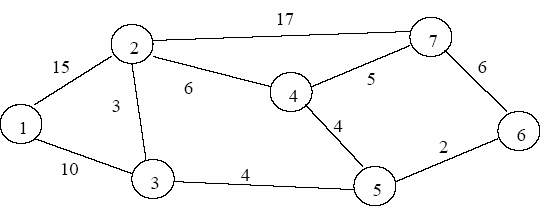Рисунок 2.1. Исходные данные задачи

Для решения задачи в процедуре Excel «Поиск решения», представим ее как транспортную задачу с промежуточными пунктами. Будем считать, что транспортные расходы при перевозке одной единицы груза равны (в условных единицах) расстояниям между вершинами. Одна единица груза отправляется из вершины 1 (исходный пункт) и должна прибыть в вершину 7 (пункт назначения). Вершины 2, 3, 4, 5, 6 рассматриваются как промежуточные пункты, которые являются одновременно и исходными пунктами и пунктами назначения.

Требуется определить такую последовательность вершин, по которым должна перемещаться единица груза, отправленная из вершины 1, при которой стоимость транспортных расходов будет минимальна и груз попадет в вершину 7.

Так как транспортные расходы при перемещении груза из одной вершины в другую равны расстоянию между вершинами, то последовательность вершин, при которой транспортные расходы будут минимальными, определяет наикратчайший путь из вершины 1 в вершину 7.

Матрица транспортных расходов, соответствующая данному графу имеет вид:

Таблица 2.1

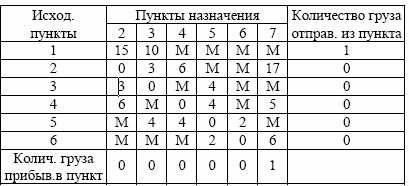
Буквой М обозначается случай, когда между соответствующими вершинами нет пути. В качестве М берут число, значительно большее самого большего пути. В данной задаче наибольший путь между 5-й и 7- ой вершинами, поэтому можно взять, например, М=100. Для промежуточных пунктов 2, 3, 4, 5, 6 должны быть предусмотрены буферные емкости (В).

Буферная емкость должна быть не меньшей, чем количество груза, которое перемещается в сети описываемой графом. В данной задаче – В=1. После введения буферных емкостей в первый столбец и нижнюю строку таблицы и замены М=100, получим транспортную задачу, представляющую задачу о назначениях.

Таблица 2.2

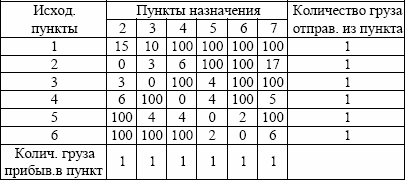
1.   В ячейках В22:G27 вводим матрицу транспортных расходов.

2.   Вводим формулы:

Таблица 2.3

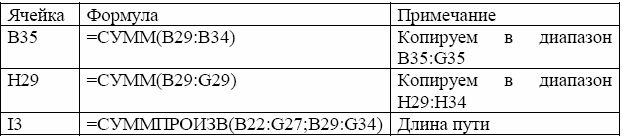
Исходные данные приведены на рисунке 2.2.

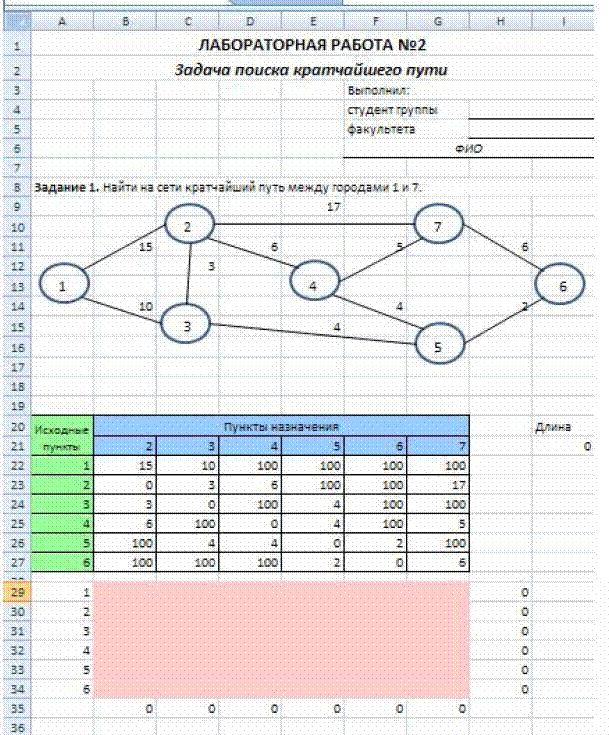
Рисунок 2.2. Исходные данные задачи

3.   Сценарий решения:

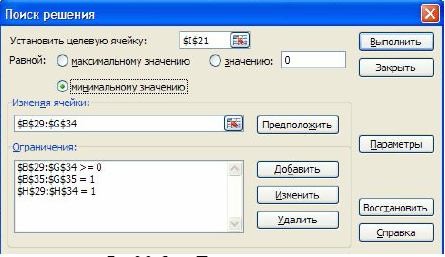
Рисунок 2.3. Окно Поиск решения.

В окне «Параметры» установить «Линейная модель», что соответствует решению задачи симплекс-методом.

4.   Он приводит к следующим результатам:

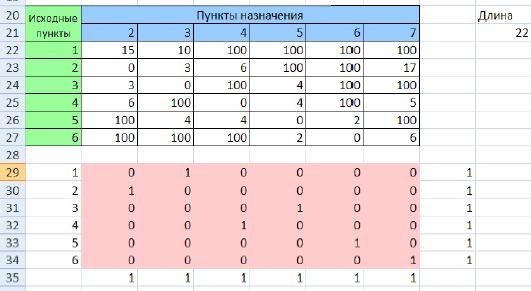
Рисунок 2.4. Результаты решения задачи

Порядок выполнения работы

1.   В соответствии с вариантом задания, определенным преподавателем, по графу составить матрицу транспортных расходов и найти ее решение.

2.   Оформить отчет о выполнении задания с приведением условия задачи, формул для расчета, результатов решения и заключения.

Варианты заданий

На рисунке показана транспортная сеть, соединяющая 16 населенных пунктов, и расстояния между ними. Найдите кратчайшие маршруты между следующими населенными пунктами:

6