Практическое применение теории графов

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ АЛТАЙСКОГО КРАЯ

КРАЕВОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «АЛТАЙСКИЙ ТРАНСПОРТНЫЙ ТЕХНИКУМ»

 

 

 

 

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

 

 

Тема:

«Практическое применение теории графов»

 

 

 

 

 

Выполнил :Пергушев Данил

 Студент 1  курса, группы АВ 93/94

профессия/специальность: Автомеханник

 

Руководитель

Утева Любовь Петровна

 

 

 

 

 

 

 

 

Барнаул 2020

 

 

 

 

 

Актуальность работы:

 

Теория графов в настоящее время является интенсивно развивающимся разделом математики. Это объясняется тем, что в виде моделей графов описываются многие объекты и ситуации, что очень важно для нормального функционирования общественной жизни. Именно этот фактор определяет актуальность их более подробного изучения. Поэтому тематика данной работы достаточно актуальна.                                                                                

Гипотеза:  Если теорию графов сблизить с практикой, то можно получить самые благотворные результаты.

Цель: Ознакомится с понятием графы, и научиться применять их  при решении различных задач.

Задачи:

1)    познакомиться с историей теории графов.

2)    изучить основные понятия теории графов и основные характеристики графов

3)    узнать о применении графов в науке и в различных сферах деятельности

4)    выделить типы задач, решение которых требует применения теории графов.

5)    рассмотреть способы решения задач с помощью графов и составить собственные задачи.

 

I.      ВВЕДЕНИЕ

 

                    Для разного рода практических задач мы используем различные методы решения. В некоторых случаях, для более быстрого, наглядного и эффективного решения задач можно использовать “Теорию Графов”.

 

II. Основная часть

Понятие графа

Теория графов – наука сравнительно молодая. «Графы» имеют корень греческого слова «графо», что значит «пишу». Тот же корень в словах «график», «биография».

В 2020 году исполняется 284 года со дня зарождения теории графов.

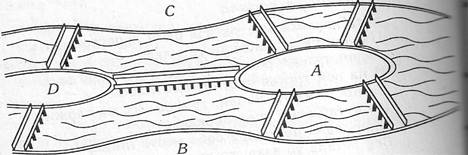
Первая работа по теории графов принадлежит Леонарду Эйлеру. Она появилась в 1736 году в публикациях Петербургской Академии Наук и начиналась с рассмотрения задачи о кенигсбергских мостах.        Вы наверное, знаете, что есть такой город Калининград, раньше он назывался Кенигсберг. Через город протекает река Преголя. Она делится на два рукава и огибает остров. В 17 веке в городе было семь мостов, расположенных так, как  показано на рисунке.

 

             

4

      Рассказывают, что однажды житель города спросил у своего знакомого, сможет ли он пройти по всем мостам так, чтобы на каждом из них побывать только один раз и вернуться к тому месту, откуда началась прогулка. Многие горожане заинтересовались этой задачей, однако придумать решение никто не смог. Этот вопрос привлек внимание ученых из многих стран. Разрешить  проблему удалось известному математику Леонарду Эйлеру. Леонард Эйлер, уроженец города Базеля родился 15 апреля, 1707 года. Научные заслуги Эйлера огромны. Он оказал влияние на развитие почти всех разделов математики и механики как в области фундаментальных исследований, так и в их приложениях. Леонард Эйлер не только решил эту конкретную задачу, но и придумал общий метод решения этих задач. Эйлер поступил следующим образом: он «сжал» сушу в точки, а мосты «вытянул» в линии. В результате получилась фигура -граф, изображенная на рисунке.

 

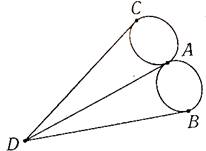
Казалось бы, ребус, детская забава — а из неё выросла целая наука — теория графов.

Графом называется конечное множество точек, некоторые из которых соединены линиями.

Точки называются вершинами графа, а соединяющие линии – рёбрами.

Вершины, из которых выходит нечетное число ребер, называют нечетными вершинами, а вершины, из которых выходит четное количество ребер, - четными.

 Свойства графа

      Если все вершины графа четные, то можно одним росчерком  ( т.е. не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии ) начертить граф. При этом движение можно начать с любой вершины и окончить в той же вершине.

      Граф с двумя нечетными вершинами тоже можно начертить одним росчерком. Движение нужно начинать от любой нечетной вершины, а заканчивать на другой нечетной вершине.

      Граф с более чем двумя нечетными вершинами невозможно начертить одним росчерком.

      Число нечетных вершин графа всегда четное.

      Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф будет равно половине числа нечетных вершин этого графа.

Например, если фигура имеет четыре нечетные, то её можно начертить, самое меньшее, двумя росчерками.

В задаче о семи кенигсбергских мостах все четыре вершины соответствующего графа нечетные, т.е. нельзя пройти по всем мостам один раз и закончить путь там, где он был начат.

 Виды графов

Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.

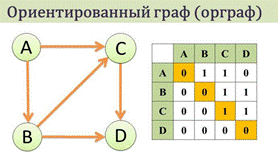
Неориентированный граф - это граф, в котором нет направления линий.

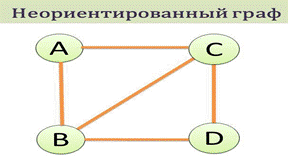
 Взвешенный граф – дуги или ребра имеют вес (дополнительная информация).

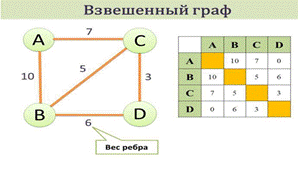
Области практического применения графов

Во многих областях человеческой деятельности можно упростить обработку информации, изображая людей, населенные пункты, химические вещества и т.п. точками и соединяя эти точки линиями или стрелками, означающими некоторые отношения. Такие схемы встречаются всюду под разными названиями:

-             социограммы (в психологии);

-             симплексы (в топологии);

-             электрические цепи (в физике);

-             диаграммы организации (в экономике);

-             сети коммуникаций;

-             генеалогические деревья.

II.Применение теории графов при решении задач

Задачи на вычерчивание фигур одним росчерком.      

Попытки нарисовать одним росчерком пера каждую из следующих фигур приводят к неодинаковым результатам.

              1                          2                  3                       4

              

               

 

 

 

 

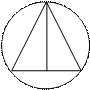
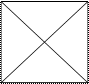
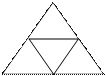
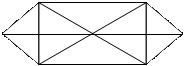
              5                                    6                                    7                                                                                                                          

              

    Если нечетных точек в фигуре нет, то она всегда поддается вырисовыванию одним росчерком пера, безразлично, с какого места ни начинать черчение. Таковы фигуры 1 и 5.

     Если в фигуре имеется только одна пара нечетных точек, то такую фигуру можно нарисовать одним росчерком, начав черчение в одной из нечетных точек (безразлично в  какой). Легко сообразить, что вычерчивание должно оканчиваться во второй нечетной точке. Таковы фигуры 2, 3, 6. В фигуре 6, например, вычерчивание надо начинать либо из точки А, либо из точки В.

     Если фигура имеет более одной пары нечетных точек, то она вовсе не может быть нарисована одним росчерком. Таковы фигуры 4 и 7, содержащие по две пары нечетных точек. Сказанного достаточно, чтобы безошибочно распознавать, какие фигуры нельзя нарисовать одним  росчерком и какие можно, а также, с какой точки надо начинать вычерчивание.                   

Логические задачи

ЗАДАЧА №1

    В первенстве группы по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис - с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько ещё осталось?

РЕШЕНИЕ:

Построим граф как показано на рисунке.

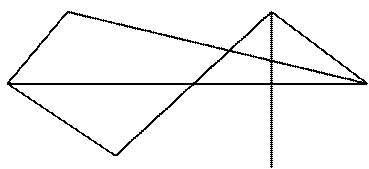
Сыграно 7 игр.

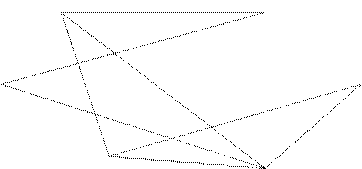
На этом рисунке граф имеет 8 ребер, следовательно, осталось провести 8 игр.

 

ЗАДАЧА №2

     Во дворе, который окружен высоким забором, находятся три домика: красный, желтый и синий. В заборе есть три калитки: красная, желтая и синяя. От красного домика проведите дорожку к красной калитке, от желтого домика – к желтой калитке, от синего – к синей так, чтобы эти дорожки не пересекались.

РЕШЕНИЕ:

Решение задачи приведено на рисунке.

           

            

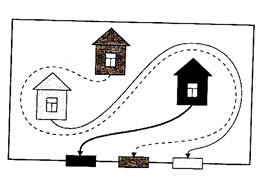
Задачи на составление оптимального маршрута

1.Сколькими способами, двигаясь по указанным отрезкам, можно кратчайшим путем переместиться из точки А в точку В?

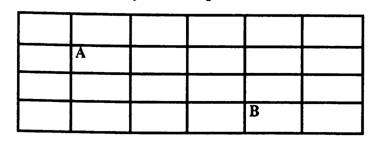
Решение  Это классическая задача на минимальный путь и возможное количество путей. Начнем с того, что вычеркнем все отрезки, лежащие вне прямоугольника с вершинами А и В. Ясно, что они не могут давать минимальный путь:

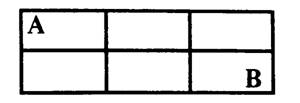
Теперь последовательно будем убирать симметричные пути:

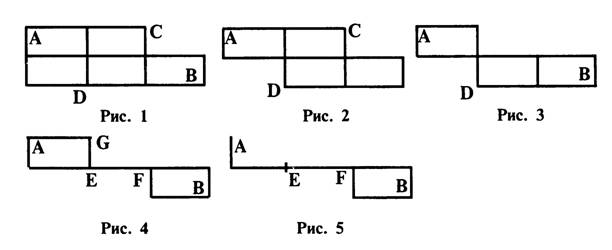
Пройдем из точки А по периметру через верхний правый угол (рис. 1), потом пройдем через левый нижний угол (рис. 2) — два пути уже получены. Обратимся к рисунку 2: пройдя через точки А и С, далее мы можем попасть в точку В двумя способами (см. рис. 3). Задача имеет симметрию. Теперь из точки В пройдем через точку D (см. рис. 3) в точку А. Ясно, что это можно сделать еще двумя способами. Пройдя из А через G и Е, мы получим еще два варианта пути. И оставшиеся два варианта представлены на рисунке 5.

Ответ: десятью способами.

Примечание. Это задача на отыскание оптимального (симметричного) решения задачи.

2. Между населёнными пунктами A, B, C, D, E, F, G построены дороги с односторонним движением. В таблице указана протяжённость каждой дороги. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).

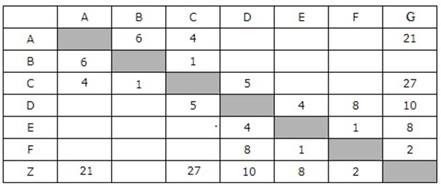
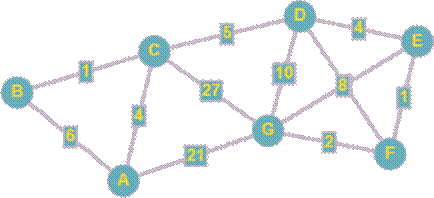
Начнем из пункта А. Из него мы можем попасть в B, С и сразу в G. Запомним, что A-G = 21. Пункт В приведет только к пункту С. A-B-C = 6 + 1 = 7, A-C = 4. Т.к. в обоих случаях мы попадаем в пункт С, выбираем наиболее короткий путь: это прямой путь A-C = 4. Из пункта C мы можем попасть в пункт D и в пункт G – нашу цель. До пункта C длина пути 4, из С в G – 27, то есть A-G = 31. Это больше, чем прямой путь, посчитанный ранее, поэтому это значение запоминать не будем. Значит, идем в пункт D. A-D = A-C + 5 = 9. Из пункта D можем попасть в E, F. Посмотрим, какой маршрут короче. Из пункта F мы можем попасть в E – и оттуда в G – и сразу в G. D-F-E-G = 8 + 1 + 8 = 17, D-F-G = 8 + 2 = 10. Из пункта E можем пойти в F – и потом в G – или сразу в G: D-E-F-G = 4 + 1 + 2 = 7, D-E-G = 4 + 8 = 12. Выбираем кратчайший маршрут: D-G = 7. Итак, A-C = 4, D-G = 7, то есть A-G = 4 + 5 + 7 (учитываем дорогу C-D) = 16. Прямая дорога A-G = 21, а A-C-D-G = 16. Значит, ответ – 16. Ответ: 16
III. Заключение

В результате работы над проектом я узнал, что Леонард Эйлер был основоположником теории графов, решил задачи с применением теории графов. Для себя сделал вывод, что теория графов находит применение в различных областях современной математики и её многочисленных приложений. Не приходится сомневаться в полезности ознакомления нас, студентов, с основными понятиями теории графов. Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность. Многие доказательства также упрощаются, приобретают убедительность, если воспользоваться графами. В особенности это относится к таким областям математики, как математическая логика, комбинаторика.

Таким образом, изучение этой темы имеет большое общеобразовательное, общекультурное и общематематическое значение. В повседневной жизни все большее применение находят графические иллюстрации, геометрические представления и другие приемы и методы наглядности. Владение, методом решения задач используя теорию графов, имеет большое практическое значение.    

 

 

 

Список используемых источников и литературы

1.     Уилсон Р.: Введение в теорию графов: учеб. пособие / Р. Уилсон.

2.     Хакари Ф.: Теория графов: / Ф. Хакари.  М.: Мир, 1973. 

3.     Кормен Т. М.и др.: Часть VI. Алгоритмы для работы с графами: / Т. М. Кормен и др.

4.     Салий В. Н., Богомолов А. М.: Алгебраические основы теории дискретных систем/  Салий В. Н., Богомолов А. М.

5.     Кирсанов М. Н. Графы в Maple/ Кирсанов М. Н. 

6.     Википедия. [Электронный ресурс]  /http://ru.wikipedia.org/

7.      Google. [Электронный ресурс] /http://www.google.ru/

8.     Альхова З.Н., Макеева А.В. «Внеклассная работа по математике».

 Журнал «Математика в школе». Приложение «Первое сентября» № 13 2008г.

9.     3. Я.И.Перельман «Занимательные задачи и опыты».- Москва: Просвещение, 2000 г.

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru