Практическое занятие №7 Аналитические модели для подсчета результатов принятия решений

Практическое занятие №7

Аналитические модели для подсчета результатов принятия решений

Существует множество аналитических моделей, используемых для подсчета результатов принятия того или иного варианта. Наиболее распространенными являются:

•    численные методы решения уравнений или их систем;

•    теория игр;

•    теория полезности;

•    теория статистических решений и т.д.

Подсчет результатов с помощью уравнений выполняется во многих случаях. Все они привязаны к конкретной области применения и поэтому систематизировать их достаточно сложно. Можно лишь отметить, что существуют области, где эти методы применяются успешно, но существуют и такие, где с их помощью не удается достичь желаемого результата.

Теория игр используется в условиях конфликтных ситуаций. Схема игры позволяет получить формулу подсчета результатов для каждого варианта. Формализация процесса игры и есть формализация процесса подсчета результатов.

Предметом теории полезности служит представление в действительных числах относительных предпочтений отдельного лица при выборе варианта из некоторого их множества. Она позволяет сравнивать полезности альтернативных решений при условии учета в каждом варианте вклада существенных факторов.

Теория статистических решений используется для формирования вариантов довольно часто. С ее помощью создаются выражения, применяющие различные распределения изучаемого случайного процесса.

Генерирование вариантов решений на основе баз знаний, которые могут быть представлены в форме семантических сетей, деревьев целей или деревьев вывода, получило широкое распространение в результате применения экспертных систем. Наиболее популярными являются правила И-ИЛИ, синтезируемые в деревья. Правила снабжаются информацией, указывающей на степень доверия, как к самому правилу, так и условиям его реализации. С помощью правил И-ИЛИ воспроизводятся процессы принятия решений в областях, где исходная информация характеризуется противоречивостью, обрывочностью, приблизительностью.

На третьем этапе, согласно сформулированному на втором этапе критерию выбора, происходят сопоставление, оценка и выбор решения на основании функции полезности.

Простейшим методом оценки, используемым в условиях определенности, является оценка с помощью таблицы «Стоимость-эффективность». Критерием выбора в данном случае выступает максимальный доход на единицу издержек. Метод требует расчета общих издержек и общих доходов по каждому из вариантов. В табл. 1 приведен пример использования" метода «Стоимость—эффективность» для оценки вариантов капиталовложений.

Таблица .1 -  Использование метода " Стоимость-Эффективность"

Вычисленное отношение доходов к издержкам показало, что вариант В₄, имеет наибольшую величину (3,2), поэтому ему присваивается первый ранг, варианту В₁ присваивается второй ранг и т.д. Очевидно, согласно критерию, который требует выбора варианта с максимальным уровнем дохода на единицу издержек, лучшим будет вариант В₄. Варианты в данном случае сопоставимы, так как результаты измеряются в одной и той же шкале (шкала отношений) и одних и тех же единицах измерения (рублях). Величины в последней графе измеряются в ранговой шкале.

Таблица «Стоимость—эффективность» может быть использована лишь в том случае, если каждый из вариантов оценивается на основе одного критерия. Если же применяется больше одного критерия, создается таблица «Стоимость—критерий» (табл. 2).

Таблица.2 - "Стоимость -Критерий»

В ней представляются варианты решений, оцениваемые с различных точек зрения. Допустим, те же четыре варианта капитальных вложений необходимо оценить с позиций трех критериев: близость расположения к железной дороге (транспортные затраты), близость расположения к водоемам (затраты на транспортировку воды), наличие в данной местности работоспособного населения (затраты на перевозку людей).

Элементами таблицы могут быть, как абсолютные величины, указывающие на издержки или доходы, так и относительные, например, ранг варианта, вычисленный на основе таблицы «Стоимость—эффективность». Будем считать что используется величина издержек, измеряемая в относительной шкале. В последней строке таблицы указываются коэффициенты значимости каждого из критериев оценки. Это та качественная информация, которая собственно и отличает систему поддержки принятия решений от формальных оптимизационных методов. Здесь лицо, принимающее решение, вносит свой опыт и знание в процесс оценки вариантов.

Распространенным методом сравнения вариантов служат оценочные баллы. Оценочные баллы нормируют, т.е. ограничивают, их значения в некотором диапазоне, например от 0 до 1. Кроме того, устанавливается закон оценки: например, сумма всех баллов должна быть равна 1.

Общая оценка каждого из вариантов рассчитывается по формуле:

О_i  =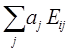

где О_i — общая оценка і-го варианта решения;

a_j — оценка j-го критерия;

Е_ij — результат, который может быть получен при і- м варианте согласно критерию j.

Тогда по варианту B₁ общая оценка равна:

O_l = E_{i i} • a_l + E₁₂ a₂+ E₁₃ a₃  = 1 78.

Наилучшим вариантом, согласно данным табл. 2, является вариант В₄. Однако абсолютные величины в большинстве случаев мало информативны. Например, издержки в сумме 153, не соотнесенные с доходами, не дают полностью объективной картины. Поэтому в большинстве случаев в качестве элементов E_tJ используют относительные величины (ранги, рентабельности, нормы прибыли и т.д.).

Кроме критериев оценки в табл. 2.2 могут указываться и условия, влияющие на результат реальных событий. Такие таблицы получили название «таблицы решений».

Таблицы решений сочетают в себе варианты решений и возможные ситуации (условия) Их элементы указывают на ожидаемый результат. Продолжая рассматривать пример о капитальных вложениях, будем считать, что в результате применения таблицы «Стоимость-критерий» выбран вариант В₄. При данном варианте возможны различные условия его реализации. В результате будут различаться и последствия. Допустим, возможны следующие факторы:

•    U₁— тарифы на энергоносители не будут превышать установ ленных границ;

•    U₂ — тарифы на водозабор не будут превышать установлен ных границ;

• U₃— работоспособного населения достаточно. Таблица решения в данном случае имеет вид (табл. 3).

Таблица.3. Таблица решений

В табл. 2. с помощью символа U_i представлено условие, отрицающее фактор U.

Таблицы решений используются в том случае, если:

•    можно выделить условия, влияющие на результаты вариантов решений;

•    выделенные условия достаточно весомы.

Деревья решений используются в условиях риска и при этом условия, определяющие варианты решения, находятся в отношениях соподчиненности. На практике это означает, что процесс принятия решения носит многоступенчатый характер: принятие одного решения на более низком уровне управления позволяет перейти к другому, более высокому уровню. Как правило, условия носят качественный характер и определяются вероятными величинами.

Иерархические отношения удобно представлять в виде дерева: дуги дерева отражают альтернативы частичных решений, а узлы — результаты. Таким образом, получают дерево решений с помощью которого можно представлять вероятностные (частотные) характеристики условий. Это позволяет достаточно просто определять результат принятия решения на том или ином уровне дерева с помощью математического ожидания:

Е(загального _ результату) =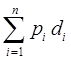

где Е (общего_результата) — математическое ожидание общего, или промежуточного, результата;

р_i — вероятность наступления события i;

d_i, — результат (частный), получаемый при наступлении события i;

n — количество событий, влияющих на общий (промежуточный) результат.

Рассмотрим пример. Допустим, лицу, принимающему решение, известны два варианта повышения уровня рентабельности на 5%:

1. Произвести продукцию А в количестве 100 ед. и продать ее по цене 10 ед. за штуку. Себестоимость единицы продукции составляет 8 ед.

2. Произвести продукцию В в количестве 50 ед. и продать ее по цене 20 ед. за штуку. Себестоимость единицы продукции составляет 18 ед.

Конъюнктура рынка неизвестна, поэтому будем считать, что рынок одинаково благоприятен для обоих видов продукции. Для упрощения задачи будем считать, что в случае неблагоприятного рынка для какой-либо продукции предприятие терпит убытки по ее себестоимости. Тогда в случае благоприятного рынка предприятие получит от продажи продукции следующий доход:

1. От продукции A: d₁ = 100 • 10 = 1000 од.

2. От продукции B: d₃ = 50 • 20 = 1000 од.

При неблагоприятном рынке оно будет убыточным:

1. От продукции A: d₂ =-100 • 8 = -800 ед.

2. От продукции B: d₄ = -50 • 18 = -900 ед.

Построим дерево решений, на котором отразим последовательность событий от корня к листьям, а затем выполним расчет доходов (убытков) в обратном направлении.

На дереве решений (рис. 2.) представлены альтернативные варианты, при которых предприятие ожидают доходы или убытки. Так как отсутствует информация о рынке, будем считать, что он одинаково благоприятен или неблагоприятен для обоих видов продукции и вероятность такого состояния рынка равна 0,5.

Рис. 2. Дерево решений производства продукции и В

Определим средний ожидаемый доход для каждого из вариантов.

1.   (дохід _ від _А) = 0,5 ·1000 – 0,5 ·800 = 100 од

2. (дохід _ від _ В) = 0,5-1000 - 0,5-900 = 50 од.

Вывод: целесообразным будет вариант 1, т.е. производство продукции А.

Можно пойти на некоторые затраты с целью получения информации о конъюнктуре рынка, что позволит уточнить, насколько рынок будет благоприятен для того или иного товара.

Допустим, в результате такого обследования получены следующие вероятности:

• ситуация будет благоприятна для продукта А с вероятностью 0,6;

• ситуация будет благоприятна для продукта В с вероятностью 0,7. Воспользовавшись формулой расчета математического ожидания получим:

1.   ( дохід _ від _ А) = 0,6 • 1000 - 0,4 • 800 = 280 од.

2.   (дохід _ від _В) = 0,7 ·1000 - 0,3 · 900 = 430 од.

В данном случае выгоднее выбрать вариант 2, т.е. производство продукции В.

Решение может формироваться не только одним лицом, но и группой лиц (экспертов). Групповые решения более точны, так как базируются на совокупном опыте группы. Мнения отдельных членов группы по поводу принятия того или иного варианта решения, как правило, не совпадают, поэтому должны использоваться специальные методы, учитывающие мнение каждого. Простейшим является метод суммирования рангов. Суть метода в следующем: каждый из участников ранжирует варианты решений в соответствии с его представлением о правильности варианта. Далее для каждого варианта подсчитывается сумма присвоенных им рангов. Выбирается вариант, получивший наибольший ранг.

Обратимся к табл. 4, где представлены результаты оценки трех вариантов решений четырьмя участниками группы оценки. Если считать, что ранг варианта снижается от 1 до 3, то наилучшим вариантом является bi, так как сумма рангов для него минимальная (7).

Таблица.4. Групповая оценка вариантов

Рассмотренные методы и модели формирования управленческих решений не затронули весьма важные аспекты данного процесса, касающиеся нравственной стороны дела. Принятие решений в любой сфере человеческой деятельности базируется на системе нравственных ценностей, усвоенной лицом, принимающим решение. Ценности условно можно разделить на собственные и нормативные, т.е. общественно признанные. У каждого человека свое отношение к общепризнанным ценностям: одни он принимает, другие нет. Однако в любом случае ему необходимо определиться в двух принципиальных позициях:

•    в главной цели, которая может быть гуманистической, корыстной, узковедомственной, общественно значимой и т.д.;

•    в средствах достижения целей, которые могут быть приемлемыми или нет в глазах общественности.

Выбор управленческих решений зависит не только от интеллектуального уровня личности, но и от его нравственно-этической позиции. Современная действительность подчеркивает особую актуальность этой проблемы во всех звеньях управления экономикой.