Практическое занятие на тему: Обратные функции и их графики. Обратные тригонометрические функции. Преобразования графика функции. Гармонические колебания. Прикладные задачи. Показательные, логарифмические, тригонометрические уравнения и неравенства.

ПЗ № 19. Обратные функции и их графики. Обратные тригонометрические функции. Преобразования графика функции. Гармонические колебания. Прикладные задачи. Показательные, логарифмические, тригонометрические уравнения и неравенства.

Задание:

1)А)Опорный конспект.

1.Определение обратной функции.

Пусть функция  строго монотонная (возрастающая или убывающая) и непрерывная на области определения , область значений этой функции , тогда на интервале  определена непрерывная строго монотонная функция  с областью значений , которая является обратной для.

Другими словами, об обратной функции  для функции  на конкретном промежутке имеет смысл говорить, если на этом интервале  либо возрастает, либо убывает.

Функции f и g называют взаимно обратными.

Пример. Найти функцию обратную для .

Решение.

Областью определения и областью значений этой функции является все множество действительных чисел. Выразим x через y (другими словами, решим уравнение  относительно x ).  - это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать .Таким образом,  и  - взаимно обратные функции.

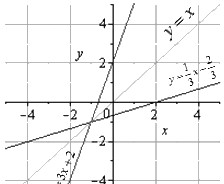
Приведем графическую иллюстрацию взаимно обратных линейных функций.

Очевидно, что графики симметричны относительно прямой y=x (биссектрисы первого и третьего квадрантов).

Перечислим свойства взаимно обратных функций  и .

 и .

Из первого свойства видно, что область определения функции совпадает с областью значений функции  и наоборот.

Графики взаимно обратных функций симметричны относительно прямой y=x.

Если  возрастает, то и  возрастает, если  убывает, то и  убывает.

Примеры нахождения взаимнообратных функций.

1)Для степенной функции  при  обратной является также степенная функция  Если заменить буквы, то получим пару взаимно обратных функций  и 

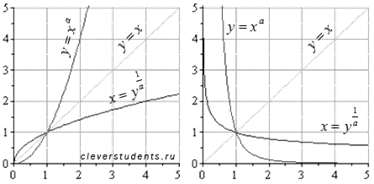
Графики для положительных а и отрицательных а.

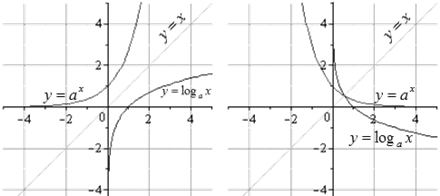
2) Взаимно обратные показательная и логарифмическая функции  и , графики.

Подразумеваем, что а положительное и не равное единице число.

Графики для  и для 

3) Обратные тригонометрические функции.

а) График  арксинуса.                     б) График  арккосинуса.

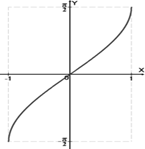  y = arcsin x  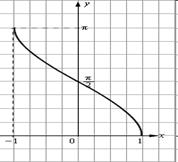y = arccos x                                                          

в) График  арктангенса .                   г) График  арккотангенса .

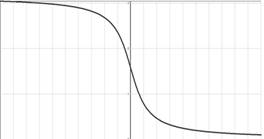         y=arcctgx

y = arctg x

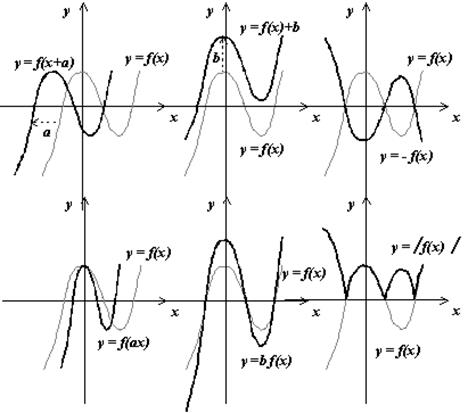
2.Преобразования графиков функций — это линейные преобразования функции y = f(x) или её аргумента x к виду y = af(kx + b) + m, а также преобразование с использованием модуля. Зная, как строить графики функции y = f(x), где y = kx + b, y = ax², y = xⁿ , y=k/x, 

y = sin x, y = cosx, y = tgx, y = ctgx, y=a^x,y=log_ax можно построить график функции y = af(kx + b) + m.

3. Алгоритм решения уравнений графическим способом            

                   Чтобы решить графически уравнение вида f(х) = g(х), нужно:

1.Построить в одной координатной плоскости графики функции: у = f(х)  и  у = g(х).

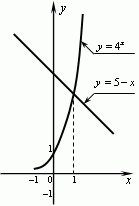2. Найти точки пересечения этих графиков.

3. Указать абсциссу каждой из этих пересечения.

4. Записать ответ. 

№ 1. Решите уравнение            

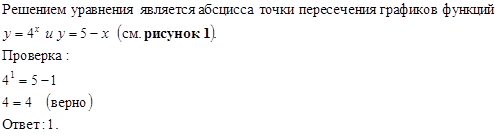
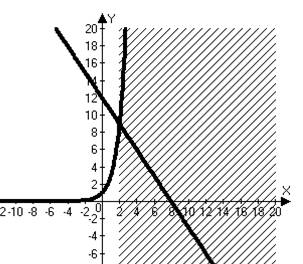
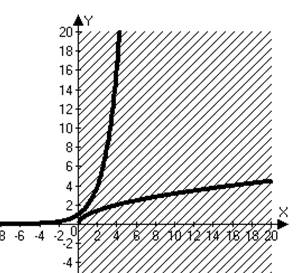
№2. Решите неравенство  >12 - 1,5х.                    №3. Решите неравенство  .                    Oтвет: х>0.                                                                         Ответ: х>2.

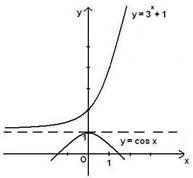№4.Решить неравенство:   сos x 1 + 3^x

Решение:

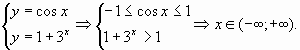
Ответ: ( ; ).

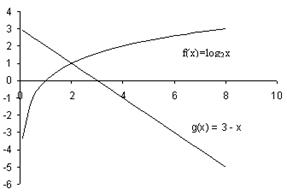
№5. Решить уравнение 

В нашем случае функция возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как .

Ответ: 2 .

Б) Построить таблицы:

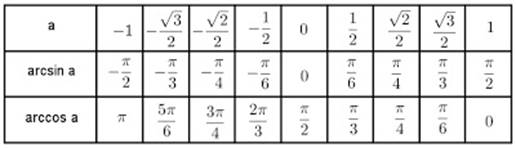
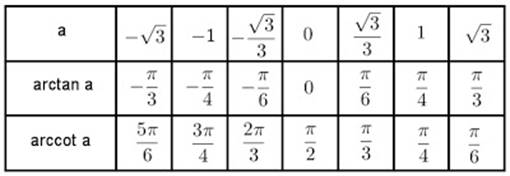
Табличные значения обратных тригонометрических функций.

В) Преобразование выражений. (Перепишите и заполните пропуски)

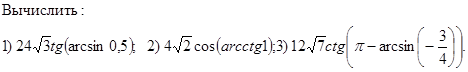
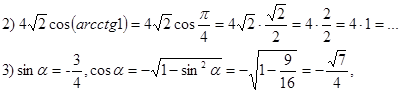
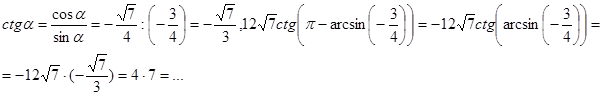
4) Вычислить  без  калькулятора

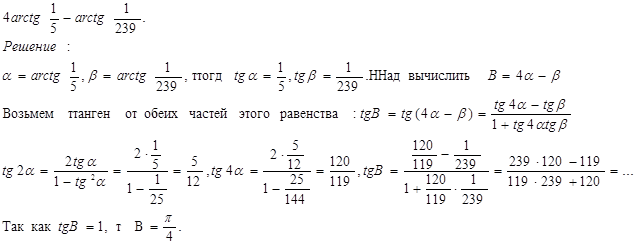
2)Решить задание ( по примерам):

1.1. Преобразование выражений

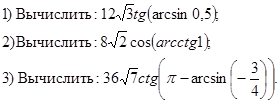
1.2.

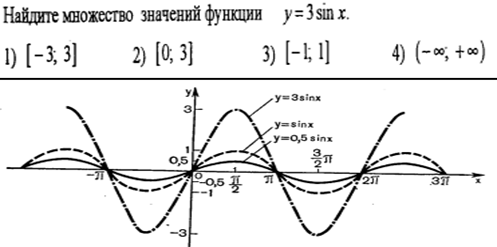
1.3.

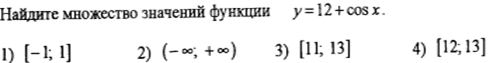
1.4.

Скачано с www.znanio.ru