Практическое занятие на тему :Построение и чтение графиков функций. Исследование функции. Свойства линейной, квадратичной, кусочно-линейной и дробно-линейной функций. Непрерывные и периодические функции. Свойства и графики синуса, косинуса, тангенса и котангенса.

ПЗ № 18. Построение и чтение графиков функций. Исследование функции. Свойства линейной, квадратичной, кусочно-линейной и дробно-линейной функций. Непрерывные и периодические функции. Свойства и графики синуса, косинуса, тангенса и котангенса.

Задание:

1)Опорный конспект.

1.1.Построение и чтение графиков.

Построение и чтение графиков должно опираться на множество практических навыков.

Приведем некоторые из рекомендованных правил при графической обработке данных и чтении графиков:

- во всякой диаграмме графический образ, как основной элемент, для которого существуют и которому подчинены все остальные элементы, должен быть в центре внимания пользователя;

- композиция диаграммы должна подчиняться правильному соотношению ее частей (согласованию их размеров, толщины, формы и положения);

- график должен быть достаточно четким, но наиболее важные его элементы должны выделяться на общем фоне в соответствии с их значением;

- вертикальную шкалу для кривой независимо от ее назначения желательно выбирать так, чтобы на диаграмме оказалась нулевая отметка;

- нулевые линии шкал для кривой следует резко отграничивать от других координатных линий;

- кривые линии диаграммы должны резко отличаться от прямых линий;

- горизонтальную шкалу для кривых следует писать слева направо, а вертикальную - снизу вверх;

- название графика располагают под ним, хотя иногда его можно писать выше диаграммы;

- общая структура графиков должна предполагать чтение слева направо;

- чтение графика следует начинать с заголовка, сообщающего, какие сведения можно из него получить. Затем надо уяснить строение графического образа и изучить специфику его элементов: шкалу, масштабы, единицы измерения, легенды и т.п., что необходимо для определения сообщаемой информации по частным вопросам. Нужно начинать восприятие графического образа как общего целого, т. е. во взаимоотношениях элементов. Затем надо увидеть выражаемое содержание графика, ясно представлять, чему соответствуют те или иные изменения графического образа.

1.2. Общие понятия.

Переменная величина y называется функцией переменной величины x, если каждому значению x соответствует определенное значение y.

Множество всех тех значений, которые принимает аргумент x функции y = f (x) , называется областью определения этой функции.

Множество всех тех значений, которые принимает сама функция y = f (x) , называется областью значений (изменения) этой функции.

Функция y = f (x)   называется четной, если при всех значений x из области определения этой функции f (- x) = f (x).

Функция y = f (x)   называется нечетной, если при всех значений x из области определения этой функции f (- x) = -  f (x).

Функция y = f (x)   называется возрастающей (убывающей)  на данном промежутке, если при произвольных двух различных значениях аргумента, из данного промежутка, большему значению аргумента соответствует большее (меньшее) значение функции.

Функция y = f (x)   называется периодической, с периодом T, где T ≠ 0, если значение функции не изменяется при прибавлении числа T к любому допустимому значению аргумента:

 f ( x +T) = f (x).

Функция y = f (x)   называется ограниченной, если можно указать такое положительное число M, что для всех значений x из области определения функции. Если же точка M не существует, то функция называется неограниченной.

Графиком функции y = f (x)   называется множество всех точек плоскости,

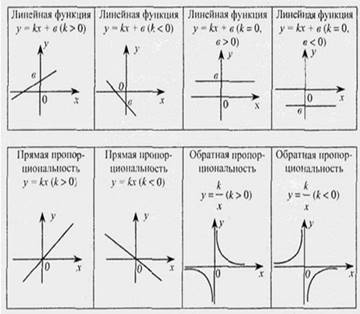
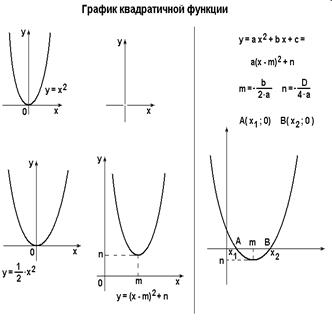
координаты которых (x, f (x)). Функцию вида y = ax² + bx + c называют квадратичной. Графиком квадратичной функции является кривая, называемая параболой.

Точку с координатами (-  b/2a, -  (b² – 4ac) / 4a) называют вершиной параболы.

Соответствие между элементами двух множеств X и Y, при котором каждому элементу множества X сопоставляется не более одного элемента Y, называется функцией.

Отсюда следует, что понятие функции имеет три главных компонента:

множество X (которое называется областью определения функции);

множество Y (которое называется областью значений функции);

закон соответствия (который иногда называется функциональной зависимостью).

При этом закон соответствия может быть задан любым способом: таблицей, графиком, формулой или как-то иначе, например, при помощи словесного описания.

Если функцию задают формулой, то при этом фактически указывают область определения функции и закон соответствия (область значений функции не указывается явно, так как она устанавливается, исходя из данной формулы).

Областью определения функции, заданной явной аналитической формулой, считают множество всех тех значений аргумента, для которых все указанные в формуле операции выполнимы.

Способы построения графиков функций.

1 способ «по точкам». 

2 способ «путем сдвига графиков основных функций или сдвига осей координат». Чтобы построить график функции y = f (x)  + c можно или график функции y = f (x)   сдвинуть вдоль оси 0y на c единиц в сторону, совпадающую со знаком c , или перенести параллельно ось 0y в сторону, противоположную знаку c.

Чтобы построить график функции y = f (x + b) , можно или график функции y = f (x)   вдоль оси 0x на b единиц в сторону, противоположную знаку b, или перенести параллельно ось 0y в сторону, совпадающую со знаком b.

3 способ, «путем симметричного отображения относительно осей координат». 

4 способ, «путем деформирования графиков основных функций». Чтобы построить график функции y =a f (x)   при a > 0, можно график исходной функции растянуть (сжать) вдоль оси ординат, если a > 1 (0 < a < 1).

Чтобы построить график функции y = f (bx)    при b > 0, можно график исходной функции растянуть (сжать) вдоль оси абсцисс, если b > 1 (0 < b < 1).

5 способ. «Кусочно-линейная функция».

Графиком кусочно-линейной функции является ломаная линия. Для построения графика находят уравнения звеньев ломаной.

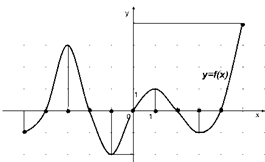Примеры графиков.

1) По  графику  найдите:

а)Какова область определения функции?

б)Назовите множество значений функции.

в)Назовите нули функции.

г) Назовите точки максимумов функции.

д)Назовите точки минимумов функции.

Ответ:

а) ,б) ,в) – 4, - 2,0,2,4 , г) – 3 ;1, д) – 1 ;3.

2) Построить график функции  на основании результатов исследования функции.

Решение:

Для построения графика функции исследуем ее, придерживаясь общей схемы исследования.

1.    Нахождение области определения:

.

2.    Определение четности или нечетности:

.  Функция  — четная.

Дальнейшее исследование будем проводить для .

3.    Область изменения функции.

Если x = 1, то y = 0. Если . Следовательно, .

4.    Пересечение с координатными осями.

 Пересечений с осью 0y нет, т.к. x = 0 не входит в область определения функции.

5.    Выделение промежутков монотонности.

Для x₁ > x₂  ≥ 1 рассмотрим разность:

.

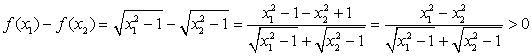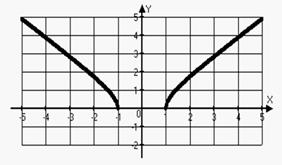При возрастании значений x от 1 до ∞ значения y возрастают.

6.    Нахождение корней функции и промежутков знакопостоянства.

Если  при x = 1,  при всех .

По результатам исследований строим график функции 

3)

4) Построить графики функции:

а) y = sin x                                                                                              в) у = tg x

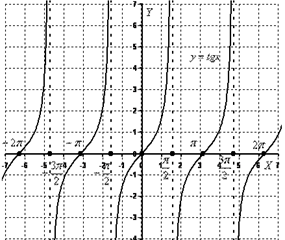
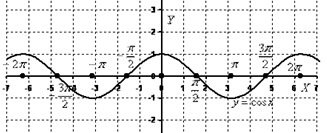
б) y = cos x

2)Решить задание:

1.    Функция задана формулой . Найдите значение , при котором () =0.

2.    Определите при каких значениях  существует функция .

3.    Постройте график квадратичной функции:   

4.    Определите при каких значениях  существует функция .

5.    Функция задана формулой . Найдите (-5).

6.    Функция задана формулой . Найдите (-3).

7.    Функция задана формулой . Найдите значение , при котором () =0.

8.    Постройте график функции у = 2х + 3 .    

9.    Проходит ли график функции у = через точки  А(13; 196 );    В(7; 49);  С(–10; 100).

10.  Постройте график у = найдите:

а) значение y, если  х = 10; х = – 8;

б) значение x, если у = 11;у = – 7.

11.  Постройте график функции у = – 2х

12.  Функция задана формулой . Найдите (-3).

13.  Функция задана формулой . Найдите значение , при котором () =0.

14.  Вычислите координаты точек пересечения параболы и прямой:

      .

15.  Найдите область значения функции .

16.  Для каждой функции, заданной формулой, укажите график.

               1) у = х – 1                     2) у = – х + 1                      3) у = х² – 1

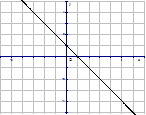
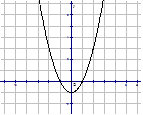
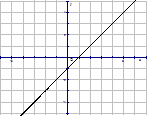
                          а)                                       б)                                    в)

17.  Постройте график функции: .

18.  Функция задана формулой f(х) = - 2х –12. Найдите: а) f(0); б) f(2); в) f(- 3); г) f().

19.  Функция задана формулой f(х) = . Найдите: а) f(0); б) f(2); в) f(- 3); г) f().

20.  Постройте график функции у = х +2. При каких значениях х выполняется неравенство ?

21.  С помощью формул описано изменение температуры воды в баке (в ⁰С) как функции времени t (в минутах):                            

                                                2t + 20, если 0 ≤ t < 40,

                                 p =       100, если 40 ≤ t < 60,

                                             t + 140, если 60 ≤ t ≤ 150.

Найдите: р (20); р (40); р (50); р (60); р (90). Постройте график функции р = f (t). Какой физический смысл имеет рассматриваемый процесс в каждом из промежутков [0;40], [40;60], [60;150]?

22.    Известно, что g(х) = 2х – 6. Найдите значение х, при котором: а) g(х) = 0; б)  g(х) = - 8.

23.    Найдите х, при котором  функция пересекает ось  ох: а) y = cos x при ,

б) y = sin x  при,в) у = tg x при .

24.    Построить график функции по таблице: а) y = 6cos x .   б) y = 4sinx 

25.    Построить график функции y = ctg x ;  запишите свойства этой функции, используя свойства функции y = tg x, и то что эти функции взаимо обратны.

Скачано с www.znanio.ru