Практическое занятие на тему :Примеры зависимостей между переменными в реальных процессах из смежных дисциплин. Определение функций.

ПЗ № 17. Примеры зависимостей между переменными в реальных процессах из смежных дисциплин. Определение функций.

Задание:

1) Опорный конспект.

А) Примеры применения различных функций  в жизни, технике, природе.

Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу x из множества D сопоставляется по некоторому правилу единственное число y, зависящее от x.  Принято называтьx независимой переменной или аргументом, а у — зависимой переменной или значением функции.

Записывают указанное соотношение между x и у в общем виде так: у = f (x) или у = F (x) и т. п.

График функции y = f (х) - это множество всех точек плоскости, координаты (х, у) которых удовлетворяют соотношению y = f(x).

Способы задания функции:

1)   аналитический (с помощью формулы);

2)   графический;

3)   табличный;

4)   словесный.

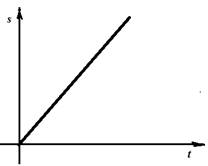
а) Линейная функция

Функция y = a x + b называется линейной потому, что ее график есть прямая линия. Характеристическим свойством линейной функции является изменение функции пропорционально изменению аргумента. Поэтому с помощью линейной функции описываются пропорциональные зависимости. Например, при равномерном движении с постоянной скоростью v пройденный путь s пропорционален времени t и выражается формулой s = v t, т.е. s – линейная функция t.

Пример линейной функции дает зависимость между различными шкалами температур. Абсолютная температура Т (по Кельвину) связана с температурой t ^ͦ C на шкале Цельсия формулой t = T + 273 ^ͦ. Другой пример – напряжение в электрической цепи прямо пропорционально силе тока U = IR. Можно много приводить примеров линейных зависимостей в физике, химии. Рассмотрим задачу на линейное расширение тел.

Задача. При температуре 0 ^оС рельс имеет длину l₀= 12,5 м. при возрастании температуры происходит тепловое расширение рельса и его длина, выраженная в метрах, меняется по закону l(t^о) = l₀(1 + t^о),где = 1,2 ˖ 10^–5 – коэффициент теплового расширения в градусах Цельсия в минус первой степени, t^о – температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм. Ответ выразить в градусах Цельсия.

Решение. Выразим из заданной формулы t:    .

Заметим, ,

тогда

Ответ: 40.

б) Квадратичная функция

Графиком квадратичной функции

 является парабола.

Хорошо известно, что траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Однако мало кто знает, что зона достижимости для пущенных нами камней вновь будет параболой. В данном случае мы говорим об огибающей кривой траекторией камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью. Если рассматривать такую огибающую в пространстве, то возникнет поверхность, образованная вращением этой параболы вокруг ее оси. Такая поверхность носит название параболоида вращения.

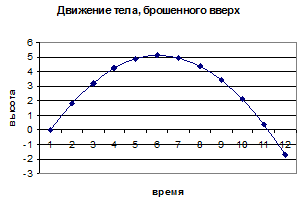
Задача. Высота над замлей подброшенного вверх мяча меняется по закону , где h — высота в метрах, t — время в секундах, прошедшее c момента броска. Сколько секунд мяч будет находиться на высоте не менее трёх метров?

Решение. Решим неравенство,

, , t₁ = 1,4,  t₂ = 0,2

0,2  ≤ t ≤ 1,4

t = 1,4 - 0,2 = 1,2

                                                         Ответ: 1,2

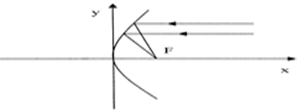Парабола обладает оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно ее оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения.            

Б)Функциональные зависимости в повседневной жизни

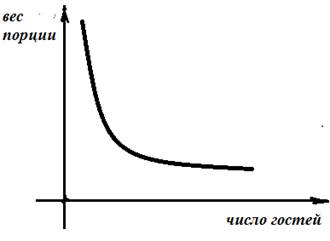
Пример 1. Рассмотрим деление праздничного торта между гостями. Отчего зависит количество порций?– от числа гостей. А от чего зависит вес порции? – тоже от числа гостей.

− В первом случае, чем больше гостей, тем на большее количество порций мы должны разделить торт (рис. 1).

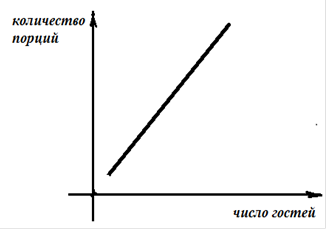
Здесь наглядно можно представить прямую пропорциональную зависимость.

Во втором случае, чем больше гостей, тем меньше вес порции. Здесь мы видим обратную пропорциональную зависимость (рис. 2).

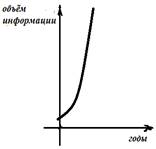Пример 2. Мы живём в век информационных технологий. Ежедневно мы получаем массу информации из различных источников: телевидения, радио, газет, журналов, и, конечно, из Интернета. Известно, что объём информации каждые пять лет увеличивается в два раза.

Если построить график зависимости объёма информации от времени, то получим некоторую кривую, которая в математике называется экспонентой и является графиком показательной функции (рис. 3).

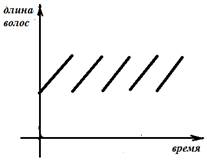Пример 3.На голове человека растут волосы, которые регулярно  стригут.

График полученной зависимости (при условии, что стрижку делают регулярно) похож на функцию дробной части числа, смещённую на aединиц вверх:   (рис. 4).    

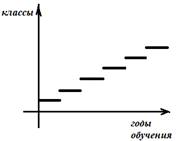
Пример 4. За время обучения в школе каждый год переходим в следующий класс.

 Такая зависимость сходна с функцией целой части числа  на ограниченном промежутке  (рис. 5).

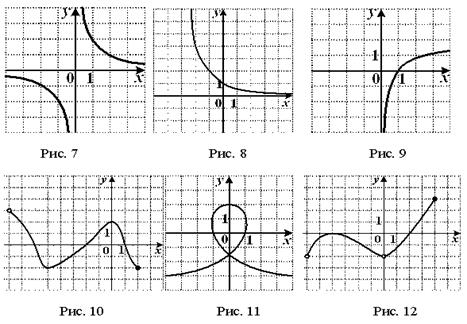
Пример 5. По графикам оценить

множество значений каждой из

представленных функций.          

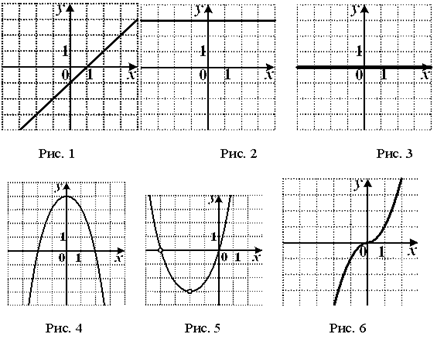
Ответ:

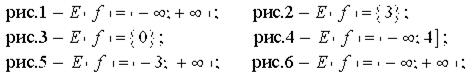
2)Решить задание:

1)

2) Функция задана формулой f(х) = - 5х – 2. Найдите: а) f(0); б) f(2); в) f(- 3); г) f().

3) Известно, что g(х) = 12 – 4х. Найдите значение х, при котором: а) g(х) = 0; б) g(х) = - 8.

4) Функция задана формулой f(х) = . Найдите: а) f(0); б) f(2); в) f(- 3); г) f().

5) Постройте график функции у = х +3. При каких значениях х выполняется неравенство ?

6) С помощью формул описано изменение температуры воды в баке (в ⁰С) как функции времени t (в минутах):                            

                                                2t + 20, если 0 ≤ t < 40,

                                 p =       100, если 40 ≤ t < 60,

                                             t + 140, если 60 ≤ t ≤ 150.

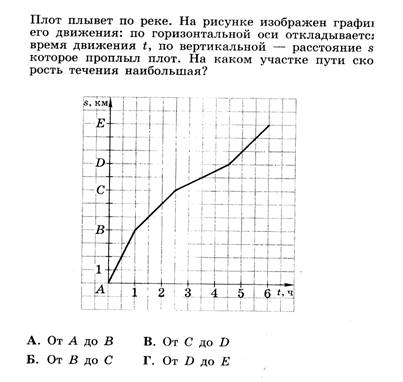
Найдите: р (20); р (40); р (50); р (60); р (90). Постройте график функции р = f (t). Какой физический смысл имеет рассматриваемый процесс в каждом из промежутков [0;40], [40;60], [60;150]?

7) Известно, что g(х) = 2х – 4. Найдите значение х, при котором: а) g(х) = 0; б)  g(х) = - 8.

8) Зависимость расстояния s (в километрах) велосипедиста до базы от времени его движения t (в часах) задана следующим образом:    

                                                                                       2t + 20, если 0 ≤ t < 40,

                                                                       s  =       100, если 40 ≤ t < 60,

                                                                                    t + 140, если 60 ≤ t ≤ 150.

Найдите: s (0); s (1); s (1,4); s (2). Постройте график функции s = f (t) (масштаб по оси t: 1 ед. – 6 клеточек; по оси s: 10 ед. – 4 клеточки). Опишите, как происходило движение велосипедиста.

9) По графикам оценить множество значений каждой из представленных функций.        

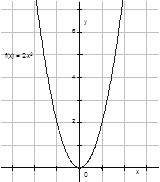
10) 1. По графику функции у = 2х² найдите:

а) значение функции, если х = 10; х = – 12;

б) значение аргумента, если у = 4; у = – 5.

2. Постройте график функции у = – 0,5х²

11) Садово-огородные процессы тоже можно представить в виде функции и построить график. К примеру, яблоко росло, зрело, потом его высушили. Постройте эту кусочную функцию.

12) Постройте график функции:

.

13) Вычислите координаты точек пересечения параболы и прямой:

      .

14) Постройте график функции:

      .