Практическое занятие на тему:Арифметические действия над числами, нахождение приближенных значений величин и погрешностей вычислений (абсолютной и относительной), сравнение числовых выражений.

ПЗ № 11. Арифметические действия над числами, нахождение приближенных значений величин и погрешностей вычислений (абсолютной и относительной), сравнение числовых выражений.

1)Опорный  конспект.

В процессе вычислений весьма часто приходится иметь дело с приближенными числами. Пусть А — точное значение некоторой величины, называемое в дальнейшем точным числом А. Под приближенным значением величины А, или приближенным числам, называется число а, заменяющее точное значение величины А. Если а < А, то а называется приближенным значением числа А по недостатку. Если а > А, — то по избытку. Например, 3,14 является приближенным значением числа π по недостатку, а 3,15 — по избытку. Для характеристики степени точности данного приближения пользуются понятием погрешности или ошибки.

Погрешностью Δа приближенного числа а называется разность вида

Δа = А — а,                                                              (1.1)

где А — соответствующее точное число.

Определение. Абсолютной погрешностью А приближенного числа а называется абсолютная величина погрешности этого числа

Δ = |А — а|.                                                               (1.2)

В силу того, что точное число А, как правило, неизвестно, то пользуются понятием предельной абсолютной погрешности.

Определение. Предельной абсолютной погрешностью Δ_a приближенного числа а называется число, не меньшее абсолютной погрешности этого числа, т. е.

Δ_a ≥ Δ.                                                                       (1.3)

Из (1.3) имеем

Δ_a ≥  |А — а|,

следовательно,

а - Δ_a £ А £ а + Δ_a,                                                   (1.4)

т. е. а - Δ_a является приближением числа А по недостатку, а а + Δ_a — приближением числа А по избытку. Формулу (1.4) кратко записывают в виде А = а ± Δ_a.

На практике под точностью измерений обычно понимают предельную абсолютную погрешность. Например, если расстояние между двумя пунктами, равное S = 900 м, получено с точностью до 0,5 м, то точное значение величины S заключено в границах 899,5 м £ S £ 900,5 м.

Введение абсолютной или предельной абсолютной погрешностей совершенно недостаточно для характеристики степени точности приближенных чисел. Существенным показателем точности приближенных чисел является их относительная погрешность.

Определение. Относительной погрешностью δ приближенного числа а называется отношение абсолютной погрешности Δ этого числа к модулю соответствующего точного числа А (А ¹ 0)

.                                                                     (1.5)

Определение. Предельной относительной погрешностью приближенного числа а называется число δ_а не меньшее относительной погрешности этого числа, т. е.

δ_а ≥ δ.                                                                        (1.6)

Из (1.6) имеем Δ £ |А|δ_а

Следовательно, можно считать, что предельная абсолютная погрешность числа а равна

Δ_а £ |А|δ_а.                                                                  (1.7)

Если принять А » а, то формула (1.7) примет вид

Δ_а £ |а|δ_а.                                                                  (1.8)

Следовательно, точное число А  лежит в следующих границах:

а(1 - δ_а) £ А £ а(1 + δ_а).

Формула (1.8) позволяет определять предельную абсолютную погрешность по заданной предельной относительной погрешности и наоборот.

Пример 1. Округляя точные числа  до трех значащих цифр, определить абсолютную  и относительную погрешности полученных приближенных чисел.

Дано:   . Найти: 

Решение:

- приближенное значение числа A

Абсолютная погрешность: 

Относительная погрешность: 

Ответ: ; 

Пример 2. Определить абсолютную погрешность приближенных чисел  по их относительной погрешности .

Дано:  .    Найти: 

Решение:

Абсолютная погрешность: 

Ответ: 

Пример 3 . При измерении длины с точностью до 5 м получено  км, а при определении другой длины с точностью до 0.5 см, получено  метров. Какое измерение по своему качеству лучше?

Дано: Км, М, М, См

Сравнить:  и 

Решение: Итак, по 1-му измерению, результат Км = М с точностью до М ( - абсолютная погрешность величины ).

Тогда относительная погрешность: %

По 2-му измерению, результат Км с точностью до См =М ( - абсолютная погрешность величины ).

Тогда относительная погрешность: %

Так как , то измерение  можно считать по качеству лучше, чем .

Ответ: измерение  по качеству лучше, чем .

2)Решить задание:

А)Вычислить:

1.        а) (– 2,35 – 4,65) · 5 : (16,9 – 2,9),    
           б) (7,63 + (– 5,13)) · 0,4 : (3,17 + 6,83),

2.        а) 30,3 · (124,9 – (48,96 : 6,8 + 36,04) : 9,2),

       б) 73, 2 · 48, 3 – 37,4 · (166,02 + 219,38) : 1,64,

3.        а) 3,44 : 0,4 + 24,56 ,     б) 684 · 245 – 675 · 246,

4.        а) (93 · 7 + 141) : 72 ,     б) 7091 + 9663 – (243916 + 75446) : 527 : 3,

       в) (15,964 · 5,2 – 12) · 0,1 ,     г) (96,6 + 98,6) : 6,4 · 1,2 – 0,2,

5.        а) ((27,12+ 43,08) · 0,007 – 0,0314) · 100,    
            б) 1,53 · 54 – 0,42 · (512 – 491,2) + 1,116,

       в) (867000 : 2125 – 396,4) · 2,15,

6.        а) 51,6 + (70,2 – 4,4 · (73,73 : 7,3)) · 1,6,    
           б) 18,305 : 0,7 – 0,0368 : 0,4 + 0,492 : 1,2,

       в) (0,6739 + 1,4261) · 557, 55 : (16,7 · 2,9 – 42,13),    

       г) 702,3 – (59 – 389,64 : 6,8) · (59,3 – 5,64 : 9,4),

7.        а) 316219 – (27090 : 43 +16422 : 119),     б) 565,3 – 465,3 : ((1,25 + 5,8) · (55,8 – 49,2)),

       в) 74 : 100 – 0,4 : 10 + 17,8 : 1000,     г) 0,35 · 10 + 0,0237 · 100 – 0,00087 · 1000,

8.        а) 0,7 : 0,1 + 0,0474 : 0,01 – 0,00174 : 0,001,     б) 12,3 + 7,7 · 187,2 : 4,5 : 6,4 – 3,4,

       в) 10,1 + 9,9 · 107,1 : 3,5 · 6,8 – 4,85,     г) 37 · 0,01 – 0,2 · 0,1 + 8,9 · 0,001.

9.        Найди значения выражений:
            а) (18370+23679):7, 156-96:(12:4):2,     б)  (800035 – 784942)∙6,

       в) 98560:7 ,83216:4, 8656:4 ,91620:4,     г) 73170:9 ,3726:9 ,91728:9, 705355:5.

10.    Найди значения выражений:
            а) (10283+16789):9, 5∙(125+75):20+80,                      б) (200496 – 134597)∙2,

        в) 54663:7, 80395:5, 6543:9, 860073:3,    г) 1836:4,7542:9, 3906:6, 9150:3,

        д)795 ·504 – 248.952:492,

11.    Реши примеры на деление:

12.    а)1098 + (1453 – 564) · 176  + 195 539– 352 004,

       б)30257 · 8  + 7 280400 · 5  – 5 897 · 6 3504: 8.

В)

1.        Найдите значение выражения:

       а) 48 – 29 + 37 – 19;  б) 156 + 228 – 193 – 66;  в) 39 • 45 : 65 • 2;  г) 1024 : 128 • 15 : 10; 
            д) 245 : 7 – 224 : 16 + 35 • 11;     е) 322 : 23 • 70 – 161 • 9 : 69; 

2.        а) 315 : (162 + 12 • 24 - 11 • 39) + 558 : 31;   б) (24 • 7 - 377 : 29) • (2378 : 58 – 38); 
            в) (120 + 16 • 7) • 240 : (300 – 5 • 44);            г) (372 + 118 • 6) : (38 • 35 – 34 • 37) - 12; 
            д) 3124 : (3 • 504 – 4 • 307) + 10 403 : 101;    е) 15 + (12 322 : (24 + 37) – 12 • 15) : (35 • 2 – 59).

3.        Измените порядок действий на основании свойств сложения, вычитания и умножения для удобства вычислений:

 а) 348 + 54 + 46;                       г) 54 • 2 • 50; 
      б) 543 + 89 – 43;                       д) 34 • 8 + 66 • 8; 
      в) 427 – 33 – 67;                        е) 135 • 12 – 35 • 12.

4.        Выполните действия по схеме .

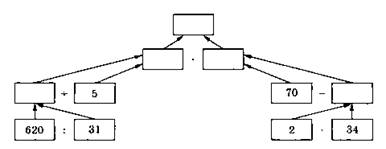
5.        Найдите частное:

а) 1 989 680 : 187;                            в) 9 018 009 : 1001; 
     б) 572 163 : 709;                               г) 533 368 000 : 83 600.

С) ТЕСТ.

D)

1.Округляя точные числа  до трех значащих цифр, определить абсолютную  и относительную погрешности полученных приближенных чисел.

Дано: А= 0,1766 ,  . Найти: .

2. Определить абсолютную погрешность приближенных чисел  по их относительной погрешности .

Дано: а =\ 4,782, .    Найти: 

3.Вычислить:

а)

б)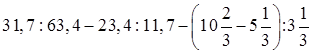

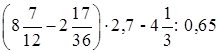
в)

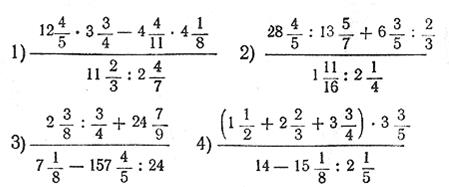
г)

д)

Скачано с www.znanio.ru