ПРАКТИЧЕСКОЕ ЗАНЯТИЕ РАЗРАБОТКА ПРОГРАММ С ИСПОЛЬЗОВАНИЕМ ВЛОЖЕННЫХ ЦИКЛОВ

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ РАЗРАБОТКА ПРОГРАММ С ИСПОЛЬЗОВАНИЕМ

ВЛОЖЕННЫХ ЦИКЛОВ

1.     ЦЕЛЬ ЗАНЯТИЯ

Целью занятия является получение навыков в составлении циклических программ с использованием вложенных циклов For.

2.     ИНФОРМАЦИОННЫЙ БЛОК

Цикл называется вложенным, если он размещается внутри другого цикла. На первом проходе, внешний цикл вызывает внутренний, который исполняется до своего завершения, после чего управление передается в тело внешнего цик- ла.

3.   ИСПОЛНИТЕЛЬНЫЙ БЛОК

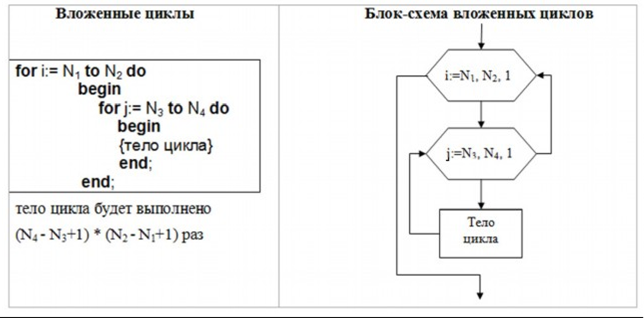
По представленным ниже блок-схемам составить программы и определить,

что они выполняют.

4.   ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ

1)       Вывести на экран таблицу умножения (от 1 до 9).

Пояснение к задаче и алгоритм решения: Перебрать во внешнем цикле числа от 1 до 9. Для каждого из них перебрать во внутреннем цикле числа от 1 до 9. Во внутреннем цикле выполнять умножение переменных-счетчиков внешнего и внутреннего циклов. Таким образом на одну итерацию внешнего цикла произойдет девять итераций внутреннего, и сформируется одна строка таблицы умножения. После каждой строки надо перейти на новую. Это делает- ся во внешнем цикле, после того как закончится выполняться внутренний.

2)       Посчитать, сколько раз встречается определенная цифра в введенной последовательности чисел. Количество вводимых чисел и цифра, которую не- обходимо посчитать, задаются вводом с клавиатуры.

Пояснение к задаче и алгоритм решения:

-          Запросить у пользователя количество вводимых чисел (n) и цифру для подсчета (d).

-          Присвоить счетчику цифр значение 0.

-          Выполнить n раз цикл, в теле которого

-         запрашивать очередное число,

-         пока это число не сократиться до нуля

-         извлекать последнюю его цифру и сравнивать с цифрой, кото- рую надо посчитать,

-         увеличивать значение счетчика цифр на 1, если сравниваемые цифры совпадают,

-         избавляться от последней цифры числа.

-          В конце программы вывести количество посчитанных цифр на экран.

3)       Вводятся десять натуральных чисел больше 2. Посчитать, сколько сре- ди них простых чисел.

Пояснение к задаче и алгоритм решения

Простым называется натуральное число (кроме 1), делителями которого являются только оно само и 1. Например, число 5 - простое, т.к. его можно на- цело разделить только на 5 и 1, а число 6 - сложное, т.к. помимо 6 и 1 делится на 2 и 3.

-          Предположим изначально, что все десять чисел простые. Присвоим счетчику простых чисел значение 10.

-          Каждое вводимое число надо проверить на делимость на все натураль-

ные числа начиная с двойки и до квадратного корня до него.

-          Если хотя бы один из делителей делит число нацело, значит число сложное и надо уменьшить счетчик простых чисел.

-          В конце программы вывести значение счетчика простых чисел. Оно будет уменьшено на количество введенных сложных чисел, следовательно, бу- дет показывать количество введенных простых чисел.

4)       Вывести на экран числа в виде следующих таблиц:

5)       Даны 20 чисел, образующие неубывающую последовательность. Не- сколько чисел, идущие подряд, равны между собой. Найти количество таких чисел. Сколько различных чисел имеется в последовательности?

Скачано с www.znanio.ru