ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ

УНИВЕРСИТЕТ»

СУДОМЕХАНИЧЕСКИЙ ТЕХНИКУМ

 

 

Цикловая комиссия физико – математических дисциплин

Уколова Ю.В.

 

 

 

 

 

 

 

 

 

 

 

 

 

ФИЗИКА

 

Практикум по лабораторным работам

для студентов (курсантов) второго курса специальностей:

 

26.02.04 «Монтаж и техническое обслуживание судовых машин механизмов»

26.02.05 «Эксплуатация судовых энергетических установок»

26.02.06 «Эксплуатация судового электрооборудования и средств автоматики»

22.02.06 «Сварочное производство»

 

 

 

 

профиля технического очной формы обучения

 

 

 

 

 

 

                                                                                               Керчь,2018                                       

          

СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ .............................................................................................................. 4

1   ПРАВИЛА ВЫПОЛНЕНИЯ ЛАБОРАТОРНЫХ РАБОТ .................................. 5

1.1   Критерии оценивания лабораторной работы .................................................... 6

1.2   Тематический план дисциплины «Физика» ...................................................... 7

1.3   Правила по технике безопасности ..................................................................... 9 2 ИНСТРУКЦИИ К ЛАБОРАТОРНЫМ РАБОТАМ ........................................... 12 2.1 Лабораторная работа №1.Определение погрешности измерений различными способами ............................................................................................................... 12

2.2        Лабораторная работа №2.Определение центра масс физического маятника и его приведенной длины ......................................................................................... 17

2.3        Лабораторная работа №3.Определение момента инерции физического маятника ................................................................................................................. 22

2.4        Лабораторная работа №4.Определение коэффициента вязкости жидкости методом Стокса ...................................................................................................... 25

2.5        Лабораторная работа №5. Определение электрической емкости конденсатора .......................................................................................................... 30

2.6        Лабораторная работа №6.Определение удельного сопротивления проводника ............................................................................................................. 37

2.7        Лабораторная работа №7. Измерение последовательного и параллельного соединения проводников. Проверка закона Ома. ................................................ 40

2.8        Лабораторная работа №8.Градуирование термопары и определение термоэлектродвижущей силы (термоэдс) ............................................................. 44 СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ................................................ 49

Приложение А.Методика определения погрешностей измерений ..................... 50

Приложение Б.Табличные данные ........................................................................ 51

ВВЕДЕНИЕ

 

Физика как естественная наука представляет собой совокупность теоретических и экспериментальных исследований. Теоретическая и экспериментальная составляющие физики развиваются взаимосвязано, взаимно дополняя друг друга. Новые экспериментальные достижения подчас требуют создания новых теорий. И наоборот, достижения в области теоретической физики создают основания для постановки новых экспериментов.

При изучении физики как учебной дисциплины важно получить навыки как экспериментальных, так и теоретических исследований. Основные навыки экспериментальных исследований в курсе физики приобретаются в рамках лабораторного практикума.

При выполнении лабораторных работ студенты (курсанты) не только применяют свои знания, развивают умения и навыки, но и учатся творчески, осознано выполнять задания, логически отвечать на контрольные вопросы, анализировать полученные результаты, делать выводы.

Основное назначение лабораторных работ, экспериментальных заданий – способствовать формированию у студентов (курсантов) глубоких и прочных знаний по физике, творческого подхода к их выполнению, развитию мышления, познавательной самостоятельности.

Каждый студент (курсант) учится выполнять простые наблюдения, измерения, опыты, обращаться с приборами, строить графики, осуществлять математические вычисления.

Данное методическое пособие предназначено для студентов (курсантов) второго курса специальностей: 26.02.04 «Монтаж и техническое обслуживание судовых машин механизмов», 26.02.05 «Эксплуатация судовых энергетических установок», 26.02.06 «Эксплуатация судового электрооборудования и средств автоматики», 22.02.06 «Сварочное производство» . 

Согласно учебной программе на выполнение лабораторных работ отводится:

Ø для специальности  26.02.04 «Монтаж и техническое обслуживание судовых машин механизмов» - 6 часов;

Ø для специальностей 26.02.05 «Эксплуатация судовых энергетических установок», 26.02.06 «Эксплуатация судового электрооборудования и средств автоматики» - 24 часа; Ø для специальности 22.02.06 «Сварочное производство» - 14 часов.

        

1 ПРАВИЛА ВЫПОЛНЕНИЯ ЛАБОРАТОРНЫХ РАБОТ

 

1.Студент (курсант) должен прийти на занятие подготовленный к лабораторной работы. На специальных листах формата A4 должно быть написано:

а) тема,  номер работы;

б) цель работы;

в) перечень оборудования;

г) схема или рисунок установки;

д) чертеж таблицы;

2.Каждый студент       (курсант)    должен       знать правила      по      технике безопасности при работе в физической лаборатории.

3.После проведения работы обучающийся должен представить отчёт и устно защитить лабораторную работу преподавателю, ответив на контрольные вопросы. 

4.Отчёт о проделанной работе следует выполнять на специальных листах формата  A4. 

5.Таблицы и рисунки следует выполнять с помощью чертёжных инструментов (линейки, циркуля, и т. д.) карандашом.

6.Расчёт следует проводить с точностью до двух значащих цифр.

При мелких исправлениях неправильное слово (буква, число и т. п.) аккуратно зачёркиваются и над ним пишут правильное пропущенное слово

(букву, число и т. п.). Вспомогательные расчёты можно выполнять на отдельных листках, а при необходимости на листах отчёта.

Если студент (курсант) не выполнит лабораторную работу или часть работы, то он может выполнить её во внеурочное время, согласованное с преподавателем.

7.Оценку по лабораторной работе студент (курсант) получает, с учётом срока выполнения работы, если:

-    расчёты выполнены правильно и в полном объеме;

-    сделан анализ проделанной работы и вывод по результатам работы;

-    студент (курсант) может пояснить выполнение любого этапа работы;  отчёт выполнен в соответствии с требованиями к выполнению работы;

-    устно защищена работа преподавателю.

Отчёт должен содержать:

1.Тема работы. 2.Цель работы.

3.Перечень необходимого оборудования.

4.Формулы искомых величин и их погрешностей.

5.Таблица с результатами измерений и вычислений.

6.Выводы о проделанной работе.

Допуск к экзамену по физике студент (курсант) получает при условии выполнения       и       устной        защите                 всех   предусмотренных         программой лабораторных работ!     

1.1   Критерии оценивания лабораторной работы

 

Уровень учебных достижений	Оценка	Критерии оценивания учебных достижений студентов (курсантов)
Начальный	2	Студент (курсант) описывает явления или часть их без объяснения причин, с помощью преподавателя отвечает на вопросы, требующие ответа «да» или «нет». Не знает теорию лабораторной работы и не понимает, как ее выполнять.
Средний	3	Студент (курсант) описывает явления, без объяснений приводит примеры, по теории базируется на собственных наблюдениях, материале учебника, объяснения преподавателя. Может выполнять лабораторную работу, снять показания приборов, заполнить таблицу.
Достаточный	4	Студент (курсант) умеет объяснять физические явления, производит анализ, обобщение знаний и их систематизацию. Работу выполняет сознательно, но вывод в работе, ответы на контрольные вопросы дает с помощью преподавателя, учебника.
Высокий	5	Студент (курсант)  свободно высказывает свои мысли, самостоятельно оценивает, аргументирует различные физические явления, имеет свое личное мнение. Умеет находить источники информации и использует полученные знания и умения при выполнении лабораторных работ, отвечает обосновано на контрольные вопросы, делает вывод.

         

1.2   Тематический план дисциплины «Физика»

 

 

Специальность 26.02.04 «Монтаж и техническое обслуживание судовых машин механизмов»

 

 

Наименование разделов	Объем аудиторных часов	Объем часов для лабораторных работ
Раздел 1 Физические основы механики.	16	4
Раздел 2 Молекулярная физика и термодинамика	8	-
Раздел 3 Электричество и магнетизм	12	2
Всего	36	6

 

 

Специальность 26.02.05 «Эксплуатация судовых энергетических установок»

 

 

Наименование разделов	Объем аудиторных часов	Объем часов для лабораторных работ
Раздел 1 Физические основы механики.	22	10
Раздел 2 Молекулярная физика и термодинамика	8	-
Раздел 3 Электричество и магнетизм	34	14
Всего	64	24

         

Специальность 26.02.06 «Эксплуатация судового электрооборудования и средств автоматики»

 

 

Наименование разделов	Объем аудиторных часов	Объем часов для лабораторных работ
Раздел 1 Физические основы механики.	30	12
Раздел 2 Молекулярная физика и термодинамика	8	-
Раздел 3 Электричество и магнетизм	26	12
Всего	64	24

 

 

Специальность 22.02.06 «Сварочное производство»

 

 

Наименование разделов	Объем аудиторных часов	Объем часов для лабораторных работ
Раздел 1 Физические основы механики.	22	6
Раздел 2 Молекулярная физика и термодинамика	12	2
Раздел 3 Основы электродинамики	36	6
Всего	70	14

           

1.3 Правила по технике безопасности

 

Общие требования.

 

1.     К проведению лабораторных работ по физике допускаются студенты (курсанты), прошедшие инструктаж по охране жизнедеятельности, медицинский осмотр, не имеющие противопоказаний по состоянию здоровья и изучившие методические указания.

2.     Студенты (курсанты) должны соблюдать правила поведения, расписание учебных занятий, установленные режимы труда и отдыха.

3.     При проведении лабораторных работ по физике возможно воздействие на студентов (курсантов) следующих опасных и вредных производственных факторов: поражение электрическим током при работе с электроприборами; термические ожоги при нагревании жидкостей и различных физических тел; порезы рук при небрежном обращении с лабораторной посудой, и приборами из стекла; возникновение пожара при неаккуратном обращении с легковоспламеняющимися и горючими жидкостями.

4.     Лаборатория физики должна быть укомплектована медицинской аптечкой с набором необходимых медикаментов и перевязочных средств.

5.     При проведении лабораторных работ по физике соблюдать правила пожарной безопасности, знать места расположения первичных средств пожаротушения. Лаборатория физики должна быть оснащена первичными средствами пожаротушения: огнетушителем углекислотным ОУ-3.

6.     О каждом несчастном случае пострадавший или очевидец несчастного случая обязан немедленно сообщить преподавателю. При неисправности оборудования, приспособлений и инструмента прекратить работу и сообщить об этом преподавателю, лаборанту.

7.     В процессе работы студенты (курсанты),  должны соблюдать порядок проведения лабораторных работ, правила личной гигиены, содержать в чистоте рабочее место.

8.     Студенты (курсанты), допустившие невыполнение или нарушение инструкции по жизнедеятельности, привлекаются к ответственности и со всеми студентами (курсанты), проводится внеплановый инструктаж.

 

Требования безопасности перед началом работы

 

1.     Внимательно изучить содержание и порядок проведения лабораторной работы, а также безопасные приемы его выполнения.

2.     Подготовить к работе рабочее место, убрать посторонние предметы. Приборы и оборудование разместить таким образом, чтобы исключить их падение и опрокидывание.

3.     Проверить исправность оборудования, приборов, целостность лабораторной посуды и приборов из стекла.

        

Требования безопасности во время работы

 

1.     Точно выполнять все указания преподавателя при проведении лабораторной работы, без его разрешения не выполнять самостоятельно никаких работ.

2.     При работе со спиртовкой беречь одежду и волосы от воспламенения, не зажигать одну спиртовку от другой, не извлекать из горящей спиртовки горелку с фитилем, не задувать пламя спиртовки ртом, а гасить его, накрывая специальным колпачком.

3.     При нагревании жидкости в пробирке или колбе использовать специальные держатели , отверстие пробирки или горлышко колбы не направлять на себя и на своих товарищей.

4.     Во избежание ожогов, жидкость и другие физические тела нагревать не выше 60-70°С, не брать незащищенными руками.

5.     Соблюдать осторожность при обращении с приборами из стекла и лабораторной посудой, не бросать, не ронять и не ударять их.

6.     Следить за исправностью всех креплений в приборах и приспособлениях, не прикасаться и не наклоняться близко к вращающимся и движущимся частям машин и механизмов.

7.     При сборке электрической схемы использовать провода с наконечниками, без видимых повреждений изоляции, избегать пересечений проводов, источник тока подключать в последнюю очередь.

8.     Собранную электрическую схему включать под напряжение только после проверки ее преподавателем.

9.     Не прикасаться к находящимся под напряжением элементам электрической цепи, к корпусам стационарного электрооборудования, к зажимам конденсаторов, не производить переключений в цепях до отключения источника тока.

10. Наличие напряжения в электрической цепи проверять только приборами.

11. Не допускать предельных нагрузок измерительных приборов.

12. Не оставлять без надзора включенные электрические устройства и приборы.

 

Требования безопасности по окончании работы

 

1.     Отключить источник тока. Разрядить конденсаторы с помощью изолированного проводника и разобрать электрическую схему.

2.     Разборку установки для нагревания жидкости производить после ее остывания.

3.     Привести в порядок рабочее место, сдать преподавателю приборы, оборудование, материалы и тщательно вымыть руки с мылом.

        

Требования безопасности в аварийных ситуациях

 

1.     При обнаружении неисправности в работе электрических устройств, находящихся под напряжением, повышенном их нагревании, появлении искрения, запаха горелой изоляции, задымлении и т.д. немедленно отключить источник электропитания и сообщить об этом преподавателю.

2.     В случае, если разбилась лабораторная посуда или приборы из стекла, не собирать их осколки незащищенными руками, а использовать для этой цели щетку и совок.

3.     При разливе легковоспламеняющейся жидкости и ее загорании немедленно сообщить об этом преподавателю и по его указанию покинуть помещение.

4.     При получении травмы сообщить об этом преподавателю, который немедленно должен оказать первую помощь пострадавшему и сообщить администрации, при необходимости помочь в отправке пострадавшего в ближайшее лечебное учреждение.

5.     Оказание первой доврачебной помощи пострадавшему при ожогах огнём, паром, горячей водой: осторожно снять одежду, перевязать обожжённое место стерилизованным материалом. При ожогах кислотами, щёлочью, реактивами: промыть обожжённое место сильной струёй воды и наложить примочку из содового раствора.

6.     Оказание первой доврачебной помощи пострадавшему при слабом кровотечении: закрыть рану стерильным материалом и плотно забинтовать. При артериальном кровотечении: наложить жгут или «закрутку» выше места раны поверх ткани одежды на время не более 1,5 (летом) или 2 часа (зимой).

7.     Оказание первой доврачебной помощи при поражении электрическим током: 

-    освободить пострадавшего от действия тока, отключив напряжение или оттащив его от проводов при помощи диэлектрических перчаток;

-    при необходимости сделать ему пострадавшему искусственное дыхание и закрытый массаж сердца (после вдувания воздуха в лёгкие пострадавшему, 5-6 раз надавить на нижнюю треть грудной клетки; за 1 мин. производить 48-50 сжатий грудной клетки и 10-12 вдуваний воздуха в лёгкие).

8.     Об        аварийной ситуации    сообщить   администрации   для    проведения расследования.

          

2 ИНСТРУКЦИИ К ЛАБОРАТОРНЫМ РАБОТАМ

 

2.1 Лабораторная работа №1

 

Тема: Определение погрешности измерений различными способами

 

Цель: изучить виды погрешностей и методы их расчета, научиться пользоваться измерительными приборами: штангенциркулем, микрометром определить плотности тел правильной геометрической формы, погрешности измерений.

Оборудование: штангенциркуль, микрометр, весы, тела правильной геометрической формы, калькулятор

 

Краткие теоретические сведения

 

При изучении физических явлений и законов большое значение имеет четкое и правильное оформление, числовая обработка результатов, построение графиков и диаграмм для установления новых или подтверждения старых законов. При достаточно высокой степени измерительной вычислительной техники в настоящее время все равно невозможно произвести измерения абсолютно точно. Поэтому истинное значение измеряемой величины всегда будет отличаться от результатов измерения и последующее использование этого значения приводит к появлению погрешностей, т.е. отклонениям или ошибкам при установлении количественного результата. Физические измерения бывают прямые и косвенные. Прямые измерения производят с помощью инструментов и приборов, шкалы которых проградуированы в единицах измерения физической величины. Косвенные измерения рассчитываются по формулам, в которые входят прямые измерения физических величин. При прямых измерениях бывают погрешности в виде:

 

Таблица 2.1 – Виды погрешностей прямых измерений

а) промахи	b) случайные	с) систематические
Грубые ошибки возникающие из- за некорректного выполнения эксперимента, несоответствия единиц измерения, неисправности оборудования, выявляются при дальнейших вычислениях	Выявляются при многократном повторении опыта при измерении одной и той же величины, одним и тем же прибором.	Ошибки, связанные с несовершенством построения опыта; к ним относятся погрешности измерительных приборов и погрешности округления

 

Оценка погрешностей при прямых измерениях

 

Предположим, что мы произвели  n  прямых измерений величины x. Обозначим через x₁ , x₂, ... x_n  результаты отдельных измерений, которые вследствие наличия случайных погрешностей будут в общем случае неодинаковыми. В теории вероятностей доказывается, что истинное значение измеряемой величины  (при отсутствии систематических погрешностей равно ее среднему значению, получаемому при бесконечно большом числе измерений, т.е.

x1 x2 x3..xn xñð õèñò                        (2.1) n

Разницу между результатом измерения и истинным (средним) значением измеряемой величины, называют абсолютной погрешностью Δх. Для каждого измерения, абсолютная погрешность рассчитывается по формулам:

 

                                                                   х1 х1 xср,

        

                                                    х2 х2 xср,                                                       (2.2)

                                                х3 х3 xср,

                                                хn хn xср.

Далее определяют среднее арифметическое значение этих погрешностей:

 

x1 x2 x3..xn xñð                 (2.3) n

и принимают его за абсолютную погрешность измерения.

Относительная погрешность – отношение средней абсолютной погрешности к среднему значению измеряемой величины:

x_ñð

                                                                                                 100%                                    (2.4)

x_ñð

Конечный результат записывают в виде:

                                                                                                     xõ_ñð õ_ñð                                            (2.5)

В данной лабораторной работе необходимо определить плотность тел правильной геометрической формы и оценить погрешность сделанных вычислений.

Плотность вещества ρ – есть физическая величина, измеряемая массой вещества в единице объема. Если масса тела m, а его объем V, то плотность тела определяется по формуле:

m

                                                                                                 _                                                         (2.6)

V

Для определения плотности твердых тел существуют различные методы, например, метод гидростатического взвешивания, пикнометра и т.д.. В данной работе речь пойдет о телах правильной геометрической формы; их объем вычисляют по известным формулам геометрии, а массу измеряют взвешиванием на электронных весах. Линейные размеры тел правильной геометрической формы определяют с помощью штангенциркуля и микрометра.

Штангенциркуль – это прибор для измерений линейных размеров с точностью от 0,1 до 0,02 мм. Штангенциркуль (Рис. 2.1) состоит из стальной линейки (штанги) 5 с миллиметровыми делениями, относительно которой перемещается рамка 4 с нониусом, и двух пар губок (ножек): неподвижных 1 и подвижных 2. При сомкнутых губках отсчет по нониусу равен нулю.

 

Рисунок 2.1 – Устройство штангенциркуля

 

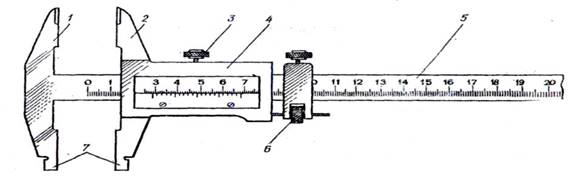
Между губками зажимают деталь. Чтобы точно определить ее размер, подвижную губку штангенциркуля перемещают до момента касания ее детали при помощи микрометрического устройства 6, чтобы избежать чрезмерного нажатия губок на деталь. Закрепляют подвижную губку на штанге стопорным винтом 3, а затем по масштабу между нулем штанги и нулем нониуса отсчитывают количество целых миллиметров. Десятые доли миллиметра определяют по делению нониуса, совпавшему с делением штанги.

Для измерения внутренних размеров детали используют калибровочные губки 7. Общая ширина их при сомкнутых губках зачастую равна 10 мм, этот размер необходимо добавлять к отсчету по шкале.

Микрометр (Рис. 2.2) – инструмент для измерения линейных размеров с точностью до 0,01 мм. Он состоит из стальной скобы 8, имеющей опорную неподвижную пяту 1, стебля 3, микрометрического винта 2 и стопорного винта

7.

 

Рисунок 2.2 – Устройство микрометра

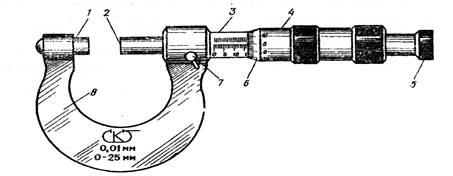
Микрометрический винт перемещается в середине специальной гильзы с резьбой, закрепленной в стебле 3. Шаг винта 0,5 – 1,0 мм.

На внешней поверхности стебля нанесены две продольные шкалы, сдвинутые одна относительно другой на 0,5 мм. Стебель заканчивается барабаном 4, соединимым с микрометрическим винтом. Таким образом, при вращении барабана вращается и винт; при этом перемещается его измерительная поверхность 2. Действие микрометра основано на особенности винта осуществлять при повороте поступательное движение, пропорциональное углу поворота. Скошенный обод барабана разделен на 50 (или на 100) одинаковых делений. На правом конце барабана есть особенное фрикционное устройство – трещотка 5. При измерении барабан необходимо вращать только за головку трещотки. Деталь при измерении зажимается между пятой и микрометрическим винтом. После того, как достигнута определенная степень нажима на деталь, фрикционная головка начинает проскальзывать, давая характерный треск. Благодаря этому зажатая деталь деформируется сравнительно мало и, кроме того, это предупреждает повреждение микрометрического винта.

Для отсчета показаний микрометра по шкале стебля определяют целое число (нижняя шкала) и половины (верхняя шкала) миллиметров.

Для отсчета сотых долей миллиметра пользуются делениями на барабане (шаг микрометрического винта определяется заранее). Перед тем как пользоваться микрометром, необходимо проверить, совпадает ли нулевое деление круговой шкалы барабана с продольным отсчетным штрихом стебля микрометра, когда соприкасаются измерительные плоскости пятки и микрометрического винта. Если же они не совпадают, следует заметить величину сдвига нулевого деления шкалы в ту или иную сторону от указанной линии и учесть ее при измерениях.

V   4 где d – диаметр,  h – высота цилиндра. Объем шара определяют по формуле:

(2.7)

Объем цилиндра определяется по формуле: d²h

                                                                                                V  r³  d³                                      (2.8)

где r – радиус,  d – диаметр  шара. Подставляя (2.7), (2.8) в (2.6), получим: для цилиндра:
4m                                                                               2					(2.9)

d h

для шара:

6m

                                                                                              ₃                                                    (2.10)

d

Для измерения линейных размеров в работе предлагается использовать штангенциркуль и микрометр, для измерения массы – весы

 

Порядок выполнения работы Задание 1.

1.            Измерьте массу m цилиндра на электронных  весах. Измерения выполните не менее 3 раз. Результаты занесите в таблицу 2.2.

2.            С помощью штангенциркуля определите высоту  и диаметр основания цилиндра. Измерения выполните также не менее 3 раз. Результаты занесите в таблицу 2.2.

 

Таблица 2.2 -  Результаты измерений для цилиндра

№	m (г)	d (мм)	h (мм)	ρ, (кг/м3)	ρср (кг/м3)	Δρ (кг/м3)	Δρср (кг/м3)	ε (%)	материал
1
2
3

 

Задание 2.

1.            Измерьте массу m шара на электронных  весах. Измерения выполните не менее 3 раз. Результаты занесите в таблицу 2.3.

2.            С помощью штангенциркуля определите диаметр шара. Измерения выполните также не менее 3 раз. Результаты занесите в таблицу 2.3.

 

Таблица 2.3 -  Результаты измерений для шара

№	m (г)	d (мм)	ρ, (кг/м3)	ρср (кг/м3)	Δρ (кг/м3)	Δρср (кг/м3)	ε (%)	материал
1
2
3

 

Обработка результатов измерения Задание 1.

1. Рассчитайте три раза плотность вещества ρ для цилиндра по формуле (2.9), подставив соответствующие данные. 

2.Вычислите среднее значение плотности, абсолютную и относительную погрешность полученных результатов по формулам (2.1 – 2.4)  3. Полученные результаты внесите в таблицу 2.2. 

4.  Конечный результат запишите в соответствии с формулой (2.5).

5.  Сравните полученную плотность цилиндра ρ_ср с табличным значением Приложение Б, таблица Б1 и определите с какого материала он изготовлен.

Задание 2.

1. Рассчитайте три раза плотность вещества ρ для шара по формуле (2.10), подставив соответствующие данные. 

2.Вычислите среднее значение плотности, абсолютную и относительную погрешность полученных результатов по формулам (2.1 – 2.4)  3. Полученные результаты внесите в таблицу 2.3. 

4.  Конечный результат запишите в соответствии с формулой (2.5) 

5.  Сравните полученную  плотность шара ρ_ср с табличным значением Приложение Б, таблица Б1 и определите с какого материала он изготовлен.

 

 

Контрольные вопросы

 

1.  Какие физические измерения называются прямыми, какие косвенными?

2.  Назовите и охарактеризуйте виды погрешностей прямых измерений?

3.  Чему равно истинное значение измеряемой величины?

4.  Что называют абсолютной погрешностью?

5.  Дайте определение относительной погрешности.

6.  Как правильно записать результат измерений?

7.Для чего используют штангенциркуль?

8.       Назовите основные структурные элементы штангенциркуля.

9.       Как устроен нониус? Чему равна точность нониуса?

10.   Для чего используют микрометр?

11.   Назовите основные структурные элементы микрометра.

12.   Как определить плотность тела?

13.   Выведите формулу для определения плотности параллелепипеда, массой m , с размерами a x b х h см?

 

Рекомендуемая литература

 

[1], [2], [3], [4], [5].

 

2.2 Лабораторная работа №2

 

Тема: Определение центра масс физического маятника и его

приведенной длины

 

Цель: научиться определять центр масс физического маятника и его приведённой длины

Оборудование: физический маятник (картонная пластинка) 1 шт., штатив с отвесом, математический маятник, линейка,  секундомер, электронные весы.

 

 

 

Краткие теоретические сведения

 

Обычно под маятником понимают тело, совершающее колебания под действием силы тяжести. При этом ось маятника не проходит через центр тяжести тела. Простейший математический маятник (Рис. 2.3), представляет  собой тело, размерами которого по сравнению с длиной нити, на которой тело подвешено, можно пренебречь. Период колебаний такого маятника зависит от его длины: 

                                                                                                 T 2                                               (2.11)

где g = 9,8 м/с² ,  l – длина нити

 

Рисунок 2.3 – Математический маятник

 

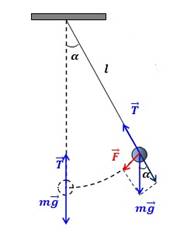
Математический маятник – это модель системы, совершающей гармонические колебания. Свободные колебания математического маятника при малых углах отклонения описываются уравнением гармонических колебаний.       _r

В положении равновесия сила тяжести mg и сила упругости (сила r

натяжения нити) T нити уравновешивают друг друга, и материальная точка находится в покое. При отклонении материальной точки от положения r равновесия на малый угол α на тело будет действовать возвращающая сила F , которая является тангенциальной составляющей силы тяжести:

Эта сила сообщает материальной точке тангенциальное ускорение, направленное по касательной к траектории, и материальная точка начинает двигаться к положению равновесия с возрастающей скоростью. По мере приближения к положению равновесия возвращающая сила, а следовательно, и тангенциальное ускорение точки, уменьшаются. В момент прохождения положения равновесия угол отклонения α=0, тангенциальное ускорение также равно нулю, а скорость материальной точки максимальна. Далее материальная точка проходит по инерции положение равновесия и, двигаясь в направлении, r противоположном силе F , сбавляет скорость. В крайнем положении материальная точка останавливается, и затем начинает двигаться в обратном направлении.

Физическим маятником называется твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки не совпадающей с его центром масс.

Центр масс — это геометрическая точка, положение которой характеризует распределение масс в теле.

При малых углах отклонения (Рис.2.4) физический маятник также совершает колебания, близкие к гармоническим, с периодом 

J

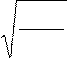                                                                                     T 2                                                           (2.12)

mgl

где l –расстояние от точки подвеса О до центра масс С; m − масса тела;

J – момент инерции относительно оси, проходящей горизонтально через точку подвеса О.

 

 

Рисунок 2.4 − Физический маятник

 

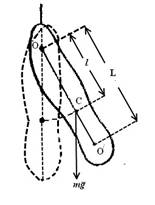
Точка О^/ на продолжении прямой ОС, находящаяся на расстоянии L от оси подвеса, называется центром качания маятника, а точка С – центр масс физического маятника При этом расстояние ОО^/ = L всегда больше ОС =l.Точка О оси подвеса маятника и центр качания О^/ обладают свойством взаимности. Если ось подвеса сделать проходящей через центр качаний, то точка О, прежней оси подвеса, станет новым центром качаний и период колебаний  маятника не изменится. 

Расстояние L, между точкой подвеса и О и центром  качания О^/, называют приведенной длиной физического маятника.

J

L                                                  (2.13) ml

При подстановке последнего выражения в формулу 2.12, получим:

L

                                                                                                  T2                                                     (2.14)

g

Сравнивая (2.14) и (2.12), видим, что период колебаний физического маятника совпадает с периодом колебаний математического маятника, если L=l. Иными словами, приведенная длина физического маятника равна длине математического маятника, качающегося синхронно с физическим.

Свойства маятника широко пользуются в различных приборах: в часах, при определении ускорений тел, колебаний земной коры, в гироскопах, для определения моментов  инерции тел, и др.

 

Порядок выполнения работы

 

Задание 1 Определение центра масс физического маятника

1.Проткните физический маятник  булавкой (Рис 2.5) недалеко от края, расширьте отверстие настолько, чтобы физический маятник свободно  вращался около булавки, как около оси.

2.            Воткните булавку вместе с физическим маятником и отвесом в деревянный штатив. Отметьте место, где нить отвеса пересекает нижний край физического маятника. 

3.            Снимите физический маятник и проведите линию через прокол и отмеченную точку.

4.            Повторите пункты 1-3 для двух других точек. Три проведенные линии пересекаются в одной точке С.

 

Рисунок 2.5 − Эксперимент по определению центра масс физического маятника

 

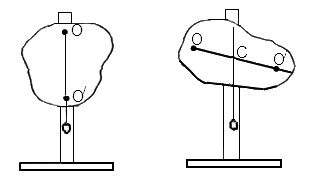
Задание 2 Определение периода и приведенной длины колебаний физического маятника.

1.            Расположите рядом с физическим маятником математический  маятник, длину которого можно изменить по ходу опыта. Добейтесь синхронного колебания математического маятника и физического.

2.            Измерьте длину математического маятника (от точки подвеса до центра тяжести), имеющего период колебания, одинаковый с периодом данного физического маятника. Эта длина L является приведенной длиной физического маятника. Отмерьте L на физическом маятнике (Рис.2.4) и найдите центр качений  т. О^/

3.Проделайте в физическом маятнике отверстие в точке О^/ и пропустите ось через эту точку. Заставьте физический маятник вновь колебаться около оси, проходящей через центр качаний. Остался ли прежним период колебаний? 

4.Определите  время 6-10 полных колебаний физического маятника, а затем 

математического маятника и  занесите в таблицы 2.4 и 2.5

5 Пункт 4 повторите еще раз

Таблицы 2.4 −Экспериментальные данные

			Математический маятник
№	N	t,c	T,c	Тср c	L, м	Lср, м
1
2

 

Таблицы 2.5 −Экспериментальные данные

			Физический маятник
№	N	t,c	T,c	Тср c	L, м	Lср, м
1
2

 

Обработка результатов измерения

 

1.Определить числовое значение периодов Т₁ и Т₂ по формуле Ò _ ^t в

N

первом и втором экспериментах для математического и физического маятников. 

2.Вычислите среднее значение периодов математического и физического маятников по формуле Ò_ñð Ò^{1 }Ò² 2

3.Измерьте приведенную длину L в каждом эксперименте и вычислите ее среднее значение.

4. Полученные данные внесите в таблицы 2.4 и 2.5

5.Сделайте вывод о периоде колебаний физического и математического маятников.

Контрольные вопросы

1.  Дайте определение математического маятников. 

2.  Назовите формулу для вычисления периода колебаний физического маятника. 

3.  От чего зависит и от чего не зависит период колебаний математического маятника?

4.  Что называется физическим маятником? 

5.  Назовите формулу для вычисления периода колебаний физического маятника. 

6.  От чего зависит и от чего не зависит период колебаний физического  маятника?

7.Что такое точка подвеса маятника?

8. Что такое центр тяжести? Что такое центр масс?

9.Сформулируйте понятие приведенной длины физического маятника и назовите определяющую ее формулу.

10.Что означает выражение «маятники синхронны»?

 

Рекомендуемая литература

 

[1], [2], [3], [4], [5].

 

2.3 Лабораторная работа №3

 

Тема: Определение момента инерции физического маятника

 

Цель: научиться определять момент инерции физического маятника

Оборудование: физический маятник (картонная пластинка), штатив с отвесом, математический маятник, линейка,  секундомер, электронные весы.

 

Краткие теоретические сведения

 

Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат расстояния от оси:

                                                                                                J_i m_ir_i²;                                                  (2.15)

Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс п материальных точек системы на квадраты их расстояний до рассматриваемой оси:

n

                                                                                                J m_ir_i²                                                (2.16)

i1

В случае непрерывного распределения масс эта сумма сводится  к интегралу m ²dm, где интегрирование производится по объему тела, т.е J ₀ r

m

J  _r²dV

0

Главный момент инерции — момент инерции относительно главной оси вращения проходящей через центр масс.

Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.

 

Таблица 2.6 - Моменты инерции однородных тел массой m, имеющих правильную геометрическую форму и равномерное распределение массы по объему

Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр радиуса R	Ось симметрии	mR2
Сплошной цилиндр или диск радиуса R	Ось симметрии	mR2
Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его середину	ml2
Шар радиусом R	Ось проходит через центр шара	mR2

 

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси z равен сумме момента его инерции J_с относительно параллельной оси, проходящей через центр масс С тела, и произведения массы m тела на квадрат расстояния a между осями:

                                                                                                 J_Z J_C ma²                                             (2.17)

Например, момент инерции прямого тонкого стержня длиной l относительно оси, которая перпендикулярна стержню и проходит через его конец (эта ось отстоит на l/2 от оси, проходящей через центр стержня):

 l 2 1 ml2 1

                                                  JZ  JC m2 12     4ml2 13ml2



Таким образом, величина момента инерции зависит от выбора оси вращения.

При малых углах отклонения (Рис.2.4) физический маятник также совершает колебания, близкие к гармоническим, с периодом 

J

T 2

mgl

где l –расстояние от точки подвеса О до центра масс С; m − масса тела;

J – момент инерции относительно оси, проходящей горизонтально через точку подвеса О, отсюда 

T²mgl

                                                                                                              J  ₂                                   (2.18)

4

Расстояние L, между точкой подвеса и О и центром качания О^/ (Рис.2.4), называют приведенной длиной физического маятника.

J

L   , ml

где J – момент инерции физического маятника; m – масса маятника;

l – расстояние от точки подвеса до центра масс точки С, отсюда

                                                                                                                 J  Lml                                  (2.19)

 

Порядок выполнения работы

 

Задание. Определение момента инерции физического маятника

 

1. Взвешиванием на весах определите массу физического маятника, полученные данные занесите в таблицу 2.7

2.На физическом маятнике измерьте расстояние от точки подвеса (О) до центра масс (С) l=ОС и занесите в таблицу 2.7

3.Период (Т_ср) физического маятника  и приведенную длину L=ОО^/  для маятника возьмите из таблицы 2.5 лабораторной работы 2.2.

 

Таблица 2.7 − Экспериментальные данные

 

				Физический маятник
m, кг	l=ОС, м	Т, c	L=ОО/, м	J1, кг м 2	J2, кг·м2	Jср, кг·м2	ΔJ, кг·м2	ΔJср, кг·м2	ε, %

 

Обработка результатов измерения

 

1.Определить момент инерции маятника J₁. по формуле (2.18) 

2.Рассчитайте момент инерции физического маятника J₂ по формуле (2.19) 3.Рассчитайте относительную погрешность ε момента инерции физического маятника методом среднего арифметического

 

Контрольные вопросы

 

1.Дайте определение момента инерции материальной точки, моментом инерции системы (тела)  твердого тела? 

2.Какой буквой обозначают момент инерции, в каких единицах измеряют?

3.Сформулируйте теорему Штейнера.

4.            Чему равны моменты инерции различных тел относительно оси, проходящей через центр: цилиндра,  диска,  шара, стержня.

5.            Определить момент инерции J тонкого однородного стержня длиной l = 40 см и массой m = 250 г относительно оси, перпендикулярной стержню и проходящей через: 1) середину стержня; 2) точку, отстоящую от конца стержня на 1/3 его длины; 3) точку, отстоящую от конца стержня на 1/6 его длины.

6.            Определите момент инерции сплошного однородного диска радиусом R = 40 см и массой m = 1 кг относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.

7.            Опишите метод определения момента инерции физического маятника в данной работе.

Рекомендуемая литература

 

[1], [2], [3], [4], [5], [7]

 

2.4 Лабораторная работа №4

 

Тема: Определение коэффициента вязкости жидкости методом

Стокса

 

Цель: научиться определять коэффициент вязкости жидкости по методу Стокса 

Оборудование: пластиковые шарики разного диаметра и известной плотности, мерный цилиндр заполненный водой  или другой вязкой жидкостью, секундомер, штангенциркуль.

 

Краткие теоретические сведения

 

Вязкость (ее иногда называют внутренним трением) – свойство текучих веществ (жидкостей и газов) сопротивляться перемещению одной их части относительно другой под действием внешних сил.

Количественно вязкость определяется величиной касательной силы, которая должна быть приложена к площади сдвигаемого слоя, чтобы поддерживать в этом слое ламинарного течения с постоянной скоростью относительного сдвига.

Вязкость газов и жидкостей, согласно молекулярно – кинетической теории, вызвана передачей импульса от молекул более быстро движущегося слоя к молекулам более медленного слоя, которая происходит при перемещении молекул соседних слоев вследствие теплового движения.

Различают стационарное, ламинарное, турбулентное движение жидкости (газа). При стационарном течении жидкость протекает сплошным потоком. Скорости молекул одинаковы по величине и направлению. Стационарное течение наблюдается в маловязких жидкостях, при большом сечении трубы, при небольших скоростях. При ламинарном течении частицы жидкости или газа движутся с постоянными по направлению скоростями, образуя параллельные слои, которые не перемешиваются друг с другом. Ламинарное течение наблюдается у очень вязких жидкостей или при течениях, происходящих с достаточно малыми скоростями, а также при медленном обтекании жидкостью тел малых размеров, в частности, ламинарное течение имеет место в узких (капиллярных трубках). Течение жидкости, в котором наблюдается турбулентность (завихрения) называется турбулентным. При таком течении частицы жидкости или газа совершают неупорядоченные неустановившиеся движения, что приводит к их интенсивному перемешиванию.

Между соприкасающимися слоями при различии их скоростей возникают силы направленные вдоль плоскости соприкосновения и препятствующих их относительному перемещению –силы внутреннего трения. Ньютон опытным путем установил, что сила внутреннего трения F пропорциональна площади соприкосновения движущихся слоев S и градиенту

d

скорости: dx

d^

F  S                                          (2.20) dx

где коэффициент пропорциональности η называется коэффициентом внутреннего трения исследуемой жидкости или коэффициентом динамической вязкости.  Из формулы (2.20) можно выразить коэффициент внутреннего трения:

F

                                          (2.21) d

S  dx

Это выражение позволяет определить физический смысл коэффициента внутреннего трения (коэффициента динамической вязкости).

Коэффициент внутреннего трения η – это сила внутреннего трения, возникающая между двумя соседними слоями, имеющими площадь соприкосновения S, равную единице, и движущимися относительно друг друга так, что градиент скорости равен единице.

В системе СИ единица измерения коэффициента динамической вязкости:

 ^{Н }₂^с  Пас м

 

Методика эксперимента

 

Для определения коэффициента динамической вязкости жидкости в работе используется метод Стокса, основанный на измерении скорости падения шарика в жидкости. Стокс установил, что при небольших скоростях движения, сила сопротивления, с которой действует жидкая среда на движущееся в ней твердое тело, пропорциональна коэффициенту динамической вязкости жидкости η, скорости υ движения тела относительно жидкости и характерному размеру тела l_к. Коэффициент пропорциональности зависит от формы тела. Для шара, если в качестве l взять радиус шара r, коэффициент пропорциональности оказывается равным 6π . Следовательно, сила сопротивления движению шарика в жидкостях при небольших скоростях в соответствии с формулой Стокса равна:

                                                                                           F  6r                                          (2.22)

Формула (2.22) получена в предположении, что расстояние от тела до границ жидкости, в данном опыте до стенок сосуда, значительно больше размеров тела r << R.

На падающий в жидкости шарик действуют три силы (рис. 2.6): 

–   сила сопротивления среды F , определяемая (2.22), 

–   сила тяжести 

–   выталкивающая сила Архимеда: mg   r³  g    (2.23)

ø

                                                                                                                       4         ³

                                                                                             F_A  _æ  r  g                                (2.24)

3

 

где ρ_ш и ρ_ж – плотности материала шарика и жидкости соответственно.

Второй закон Ньютона для падающего шарика запишется в виде:

d^

                                                                                             mg  F  F  m                                      (2.25)

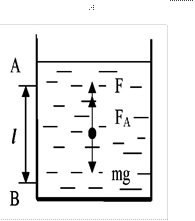dt

 

 

 

 

 

 

 

 

 

 

Рисунок 2.6 − Силы, действующие на шарик

 

Описание экспериментального исследования d

Вначале движение шарика будет ускоренным      f0, но так как сила dt

сопротивления согласно формуле Стокса увеличивается с увеличением скорости падения, то при некоторой скорости υ0 левая и правая части уравнения

движения (2.26) обратятся в нуль, и движение шарика станет равномерным

d

                                                                                                              0                                              (2.26)

dt

Параметры установки подобраны таким образом, чтобы движение шарика установилось, когда он при своем падении достигнет верхней метки А (Рис.

2.6). Тогда скорость равномерного движения определяется из соотношения: 

l

₀                                        (2.27) t

 

где l и t – расстояние между верхней и нижней метками и время, за

которое это расстояние пройдено. 

Подставляем  формулы (2.22 – 2.24) в уравнение (2.25), с учетом(2.26) получим: 

                                                                           ³                                        4         ³

                                             ø   r  g _æ  r  g  6r  0                                              (2.28)

3

откуда с учётом (2.27) находим коэффициент динамической вязкости: 

_ø _æ  g t d²

                                                                                                                      (2.29)

18l

Таким образом, определение коэффициента динамической вязкости жидкости сводится к измерению радиуса шарика и скорости его равномерного падения в жидкости, плотности материала шарика и жидкости считаются известными. 

Описание экспериментальной установки

1 – шкала мерного цилиндра; 2 – цилиндр с жидкостью; 3 – воронка; 4 – метки движения шарика в цилиндре.

 

Рисунок 2.7 − Экспериментальная установка

 

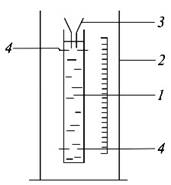
Схема установки представлена на рисунке 2.7. На цилиндрической части сосуда 2 нанесены две кольцевые метки – верхняя и нижняя 4. Расстояние между ними определяется с помощью линейки. В верхней части сосуда установлена воронка 3, обеспечивающая падение шарика вдоль оси цилиндра. Цилиндрический сосуд заливается испытываемой жидкостью 1 выше уровня верхней метки.

 

Порядок выполнения работы

 

1. Измерить диаметр d каждого шарика несколько раз и найти среднее значение и внести его в таблицу 2.8. Диаметр измеряют штангенциркулем.

2.Опустить шарик в цилиндр с жидкостью как можно ближе к его оси и в момент прохождения мимо верхней метки включить секундомер.

3.В момент прохождения шариком нижней метки  остановить секундомер.

Выполнить аналогичные измерения для всех шариков.

4.Расстояние между метками l измерить линейкой.

5.Плотности шарика и жидкости взять из таблицы Б1, приложения Б.

6.Результаты измерений занести в таблицу 2.8

 

Таблица 2.8 − Экспериментальные данные

 

										ε, %
1
2
3
4
5

 

Обработка результатов измерения

 

1.  Определить коэффициент вязкости согласно соотношению (2.29) для каждого опыта.

2.  Вычислите среднее значение вязкости 

3.  По таблице Б.2 приложения Б определите коэффициент вязкости исследуемой жидкости

4.  Вычислите абсолютную и относительную погрешности эксперимента, воспользовавшись формулами приложения А.

 

Контрольные вопросы

 

1.  Что называют вязкостью текучих веществ?

2.  Каков физический смысл коэффициента вязкости жидкости?

3.Как зависит коэффициент внутреннего трения жидкостей от температуры?

4.Какое движение  жидкости (газа) называют стационарным? ламинарным? турбулентным?

5.В чем заключается метод определения коэффициента вязкости жидкости по Стоксу?

6. Какие силы действуют на шарик при его движении в жидкости?

7.Вывести расчетную формулу для определения коэффициента вязкости.

 

Рекомендуемая литература [1], [2], [3], [4], [5], [8]     

2.5 Лабораторная работа №5

 

Тема: Определение электрической емкости конденсатора

 

Цель: экспериментальным путем определить емкость конденсатора, электроемкость батареи конденсаторов при последовательном и параллельном соединении.

Оборудование: источник питания на 4В, двойной  ключ (демонстрационный), микроамперметр, соединительные провода, конденсаторы.

 

Краткие теоретические сведения

 

Электрическая ёмкость (С) – физическая величина, характеризующая его способность накапливать электрический заряд.

Электроемкостью двух проводников равна отношению заряда q одного из проводников к разности потенциалов между ними Δφ=U: 

                                                                                                            q       q

Ñ      (2.30)  U

где q – заряд; 

Δφ=U – разность потенциалов или напряжение.

В системе СИ ёмкость измеряется в фарадах С[Ф]

Электроемкость двух проводников численно равна единице, если при сообщении им зарядов +1 Кл и  -1 Кл между ними возникает разность

Êë

потенциалов 1 В. Эту единицу и называют фарад (Ф); 1Ô 1

Â

Из-за того что заряд в 1 Кл очень велик, емкость 1 Ф оказывается очень большой. Поэтому на практике часто используют доли этой единицы: микрофарад (мкФ) – 10^-6 Ф и пикофарад (пФ) – 10^-12 Ф.

Система проводников (обкладок), разделенных диэлектриком, обладающая большой электроёмкостью при относительно небольших размерах, называется конденсатором. 

Простейший плоский конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга

(Рис.2.8)

 

Рисунок 2.8 – Плоский конденсатор

         

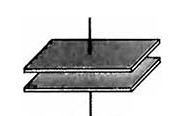
Электроемкость плоского конденсатора определяется по формуле:

                                                                                      Ñ _^0S                                                (2.31)

d

где ε – диэлектрическая проницаемость среды; ε₀ = 8,85•10^-12Ф/м – электрическая постоянная; S – площадь пластин; d – расстояние между ними.

 

Последовательное и параллельное соединения конденсаторов.

 

На практике конденсаторы часто соединяют различными способами. На рисунке 2.9 представлено последовательное соединение трёх конденсаторов.

 

Рисунок 2.9 – Последовательное соединение конденсаторов

 

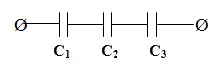
При последовательном соединении  на всех обкладках конденсаторов будут одинаковые по величине заряды q. 

                                                                                                     q_îáù q₁ q₂ q₃                                         (2.32)

Напряжение батареи конденсаторов равно сумме напряжений каждого конденсатора.

                                                                                                    U_îáù U₁ U₂ U₃                                       (2.33)

При последовательном соединении конденсаторов различной емкости, электроемкость батареи определяется по формуле:

                                                                                                       ¹  ¹  ^{1           1}                                (2.34)

_{ }... Ñîáù Ñ1 Ñ2 Ñ3

При параллельном соединении конденсаторов (рис.10) все положительно заряженные обкладки подсоединены к одному проводу, а отрицательно заряженные – к другому проводу. В этом случае заряд на батарее равен сумме зарядов на отдельных конденсаторах, а напряжения на всех конденсаторах одинаковы и равны U

q_îáù q₁ q₂ q₃                              (2.35) U_îáù U₁ U₂ U₃                  (2.36)

 

Рисунок 2.10 – Параллельное соединение конденсаторов

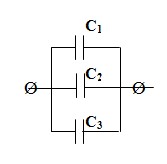
При параллельном соединении общая емкость С_общ определяется по формуле:          

                                                                                 Ñ_îáù Ñ₁ Ñ₂ Ñ₃ ..                                           (2.37)

Если заряжать конденсатор постоянной емкости от одного и того же источника постоянного напряжения, а затем разряжать его через гальванометр, то стрелка гальванометра всякий раз будет отклоняться по шкале на одно и то же число делений. При конденсаторах другой емкости гальванометр покажет другое отклонение стрелки.

Имея конденсаторы известной емкости (эталоны), можно на опыте убедиться, что величина емкости конденсатора С прямо пропорциональна числу делений n, на которое отклоняется стрелка гальванометра. 

Коэффициент пропорциональности, выражающий собой электроемкость, соответствующую одному делению определяется по формуле: n

                                                                                                                 k                                              (2.38)

C

Зная коэффициент и повторив опыт с конденсатором неизвестной емкости, можно определить его емкость по отклонению стрелки гальванометра по формуле:

n^x

                                                                                                             C_x                                             (2.39)

k

где С_х –емкость неизвестного конденсатора;

n_x – число делений на которое отклоняется стрелка гальванометра, при подключении неизвестного конденсатора в цепь.

 

Порядок выполнения работы

Часть 1

Задание 1

1.Составьте  электрическую цепь по схеме, изображенной на рисунке 2.11 . В цепи установите один из конденсаторов известной емкости.

 

Рисунок 2.11 − Экспериментальная схема задания №1

 

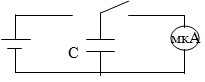
2.Конденсатор зарядите: для этого соединить его (переключателем) на короткое время с источником питания.

3.Сосредоточив внимание на микроамперметре, быстро замкните конденсатор на измерительный прибор и определите число делений, соответствующее максимальному отклонению стрелки.

4.Опыт повторить  еще два раза для более точного определения числа делений n.

5.Опыт повторите с другим конденсатором известной емкости, согласно пунктам 1-4.

6.Результаты измерений запишите в таблицу 2.9

7. Возьмите конденсатор неизвестной емкости С_х и повторить опыт(п.1-4); 8.Запишите данные n_х для конденсатора с неизвестной емкостью, полученные по микроамперметру, в таблицу 2.10.

 

Таблица 2.9 − Экспериментальные данные

 

№	Емкость конденсаторов С, мкф	Число делений по шкале микроамперметра n	Среднее число делений по шкале микроамперметра nср	Коэффициент пропорциональности n k  ñð C
1
2

 

Таблица 2.10 − Экспериментальные данные

 

№	Число делений по шкале микроамперметра nх	Найденная емкость конденсатора неизвестной емкости Сх , мкф	Средняя емкость конденсатора неизвестной емкости Схср , мкф	Стабл Схср ε =*100% Стабл
1
2
3

 

Обработка результатов измерения части 1

 

1.Рассчитайте среднее число делений n_ср для каждого конденсатора с известной емкостью.

2.Определите коэффициент пропорциональности (k) по формуле (2.38) для каждого конденсатора с известной емкостью.

3.Определите емкость С_х конденсатора с неизвестной емкостью для каждого случая по формуле (2.39). 4.Вычислите среднее значение емкости С_хср.

5.Узнайте у преподавателя табличное значение емкости исследуемого конденсатора и, приняв ее за табличное значение, определите относительную погрешность. 6.Сделайте вывод о полученной относительной погрешности.

        

Порядок выполнения работы

 

Часть 2 

Задание 1. Параллельное соединение конденсаторов

1.Составьте электрическую цепь по схеме, изображенной на рисунке 2.12, включив в нее два параллельно соединенные конденсатора известной емкости.

 

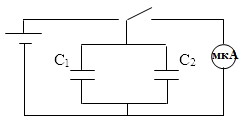
Рисунок 2.12 – Экспериментальная схема задания 1 части 2.

 

2. Батарею конденсаторов зарядите: для этого соедините их (переключателем) на короткое время с источником питания.

3.Сосредоточив внимание на микроамперметре, быстро замкните батарею конденсаторов на измерительный прибор и определите число делений, соответствующее максимальному отклонению стрелки.

4.Опыт повторить  еще два раза для более точного определения числа делений n.

Таблица 2.11 − Экспериментальные данные

 

				Коэффициент пропорциональности батареи конденсаторов n k  ñð C	Емкость батареи конденсаторов Cx1	Емкость батареи конденсаторов Cx2	ε, %

 

Задание 2. Последовательное соединение конденсаторов

1.Составьте электрическую цепь по схеме, изображенной на рисунке 2.13, включив в нее два последовательно соединенные конденсатора известной емкости.

 

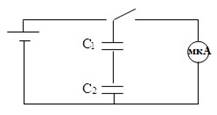
Рисунок 2.13 – Экспериментальная схема задания 2 части 2.

 

2. Батарею конденсаторов зарядите: для этого соедините их (переключателем) на короткое время с источником питания.

3.Сосредоточив внимание на микроамперметре, быстро замкните батарею конденсаторов на измерительный прибор и определите число делений, соответствующее максимальному отклонению стрелки.

4.Опыт повторить  еще два раза для более точного определения числа делений n.

Таблица 2.12 − Экспериментальные данные

 

				Коэффициент пропорциональности батареи конденсаторов n k  ñð C	Емкость батареи конденсаторов Cx1	Емкость батареи конденсаторов Cx2	ε, %

 

Обработка результатов измерения части 2

 

Задание 1. Параллельное соединение конденсаторов

1.Рассчитайте среднее число делений n_ср для батареи конденсаторов с известной емкостью.

2.Перепишите значение коэффициента пропорциональности (k) из таблицы 2.9 в таблицу 2.11

n_ñð

3.Определите емкость батареи конденсаторов С_х1 по формуле C_x1  k

4. Определите емкость батареи конденсаторов С_х2 по формуле C_x2  C₁ C₂

5.Оопределите относительную погрешность измерений по формуле:

Cx2 Cx1

  

Cx2 6.Внесите полученные данные в таблицу 2.11. 7.Сделайте вывод о полученной относительной погрешности.

 

Задание 2. Последовательное соединение конденсаторов

 

1.Рассчитайте среднее число делений n_ср для батареи конденсаторов с известной емкостью.

2.Перепишите значение коэффициента пропорциональности (k) из таблицы 2.9 в таблицу 2.12

n_ñð

3.Определите емкость батареи конденсаторов С_х1 по формуле C_x1 

k

                                                                                                                                                                              1       1      1

4. Определите емкость батареи конденсаторов С_х2 по формуле             

Ñx2 C1 C2

5.Определите относительную погрешность измерений по формуле: Cx2 Cx1



Cx2 6.Внесите полученные данные в таблицу 2.12. 7.Сделайте вывод о полученной относительной погрешности.

 

Контрольные вопросы

 

1.  Какое физическое свойство проводников называется электроемкостью?

2.  Как вычисляется электроемкость проводника? В каких единицах измеряется?

3.  Какие устройства называются конденсаторами?

4.  Какой конденсатор называется плоским?

5.  Как вычисляется электроемкость плоского конденсатора?

6.  Сформулируйте законы последовательного соединения конденсаторов.

7.  Сформулируйте законы параллельного соединения конденсаторов.

8.  В чем сущность метода определения емкости конденсатора в данной работе?

9.  Определите заряд батареи конденсаторов, соединенных так, как показано на рисунке 4.6, емкость каждого конденсатора С₁ =4мкф; С₂ =3мкф; С₃ =1мкф; С₄ =0,5мкф; С5 =0,7мкф; С6 =6мкф; С7 =6мкф; С8 =4мкф; С9 =4мкф; С10 =5мкф; С11 =2мкф.

 

 

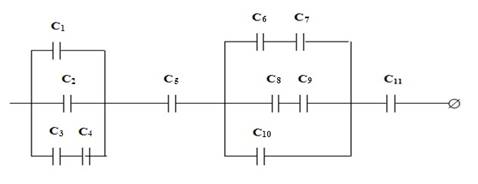
Рекомендуемая литература

 

[1], [2], [3], [4], [5], [6]

 

2.6 Лабораторная работа №6

 

Тема: Определение удельного сопротивления проводника

 

Цель: научиться опытным и расчетным путем определять удельное сопротивление проводника. 

Оборудование: источник питания, реостат, исследуемый резистор (спираль), панель с электроизмерительными приборами, соединительные провода, штангенциркуль.

 

Краткие теоретические сведения

 

Электрическое сопротивление R – физическая величина, характеризующая свойства проводника  препятствовать прохождению электрического тока.

В СИ единицей сопротивления проводника является ом (Ом). 1 Ом – сопротивление такого проводника, сила тока в котором равна 1 А при напряжении на нем 1 В.

По закону Ома сила тока I в цепи прямо пропорциональна напряжению U на её участке и обратно пропорциональна сопротивлению R этого участка, т.е

U

                                                                                                 I                                                        (2.40)

R

отсюда, сопротивление проводника R:

U

                                                                                                R                                                       (2.41)

I

Сопротивление проводника зависит от материала, из которого он изготовлен, длины проводника и площади поперечного сечения:

l

                                                                                                R                                                     (2.42)

S

где ρ – удельное сопротивление проводника, которое характеризует сопротивление 1 м провода, площадью поперечного сечения 1м². Удельное сопротивление различных материалов можно определить по таблице Б3 Приложения Б. 

Из формулы 2.42 можно вывести формулу для определения удельного сопротивления:

RS

                                                                                                                                                     (2.43)

l

Таким образом, опытным путем вычислить удельное сопротивление можно, если определить геометрические параметры проводника и сопротивление на нем.

Проводник, в данной работе представляет собой спираль с количеством витков N. Тогда, длина проводника может быть вычислена по формуле:

                                                                                            l  N 2r                                              (2.44)

где N – число витков спирали; r – радиус витка спирали.

Так как диаметр витка спирали D = 2r, то 

                                                                                           l  N  D                                              (2.45)

Площадь поперечного сечения проводника S:

d²

                                                                                                 S                                                 (2.46)

4

где d – диаметр  проволоки, из которой изготовлена спираль.

 

Порядок выполнения работы

 

1.Собрать цепь по схеме (Рис.2.14) и показать преподавателю.

2.Сделать соответствующие измерения тока и напряжения U и I, изменяя положение ползунка реостата три раза. 

3.Штангенциркулем измерить диаметр d  проволоки в трех точках, из которой изготовлена спираль и найти средне значение.

4.Определить диаметр D  витка спирали в трех точках и найти среднее значение.

5.Подсчитать число витков N в спирали добавив еще 2 витка

6. Все данные занести в таблицу 2.13

 

Таблица 2.13 − Экспериментальные данные

 

№

U, B

I, A

R, Oм

N

dср, м

Dср, м

 Oм∙м

ср Ом∙м

 Ом∙м

ср Ом∙м

ε%

Материал

1

2

3

 

 

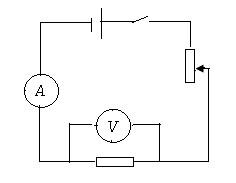
Рисунок 2.14 – Схема электрической цепи

 

Обработка результатов измерения

 

1. Вычислите длину провода l по формуле 2.45.

2.Определите сечение провода S по формуле 2.46

3.  Определите сопротивление проводника по формуле 2.41

4.  Вычислите удельное сопротивление проводника по формуле 2.43

5.  Рассчитайте погрешность измерения удельного сопротивления методом среднего арифметического

6.  Определите материал проводника по таблице Б.3 приложения Б.

7.  Запишите полученные данные в таблицу 2.13.

8.Сделайте вывод к работе.

 

Контрольные вопросы

 

1.  Какая физическая характеристика называется сопротивлением? В каких единицах измеряется?

2.  От чего зависит сопротивление проводника?

3.  Что характеризуется удельное сопротивление? 

4.  Сформулируйте закон Ома для участка цепи.

5.Какой проводник (медный или никелиновый) обладает лучшей удельной  проводимостью.

6. На рисунке изображен график зависимости силы тока в проводнике от напряжения между его концами.

 

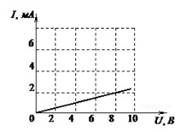
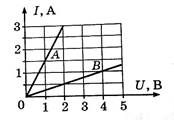
7.На рисунке приведены графики зависимости силы тока от напряжения для проводников А и В. Укажите все правильные утверждения.

1)Сопротивление проводника А больше, чем сопротивление проводника В.

2)Сопротивление проводника А меньше 0,5 Ом

3)  Сопротивление проводника В больше 5 Ом

4)  За одно и то же время при одинаковом напряжении в проводнике А выделится меньшее количество теплоты, чем в проводнике В

5)  Среди утверждений 1) – 4) нет ни одного правильного 

 

8.Сопротивление алюминиевого проводника диной 0,9 км и сечением 10 мм² равно 2,5 Ом. Определите его удельное сопротивление.

9. Определите сопротивление железной проволоки диаметром 1 мм, если масса этой проволоки 1 кг. Удельное сопротивление железа 9,8•10^-8 Ом•м, а плотность 7900 кг/м³.

 

Рекомендуемая литература

 

[1], [2], [3], [4], [5], [8]

 

2.7 Лабораторная работа №7

 

Тема: Измерение последовательного и параллельного соединения проводников. Проверка закона Ома.

 

Цель: проверка законов последовательного и параллельного соединения проводников. 

Оборудование: набор сопротивлений: 1Ом, 2Ом, 4Ом; источник питания; реостат; ключ; соединительные провода; амперметр; вольтметр.

 

Краткие теоретические сведения

 

Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. Последовательное соединение проводников.

 

 

Рисунок 2.15 – Последовательное соединение проводников

 

При последовательном соединении проводников (Рис. 2.15) сила тока во всех проводниках одинакова, т.е

                                                                                I  I₁  I₂ ..I_n                                                    (2.47)

Общее напряжение равно сумме напряжений на каждом резисторе:

                                                                               U U₁ U₂ ..U_n                                                (2.48)

Общее сопротивление равно сумме сопротивлений:

                                                                              R  R₁  R₂ ..R_n                                                 (2.49)

Параллельное соединение проводников

 

Рисунок 2.16 – Параллельное соединение проводников

 

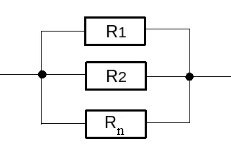
При параллельном соединение проводников (Рис.2.16) сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках:

                                                                              I  I₁  I₂.. I_n                                                    (2.50)

Напряжение U на концах проводников, соединенных параллельно, одинаковое:

                                                                               U U₁ U₂ ..U_n                                                (2.51)

Общее сопротивление при параллельном соединении:

                                                                              1      1      1        1

  ..     (2.52) R R1 R2 Rn

Тогда, общее сопротивление двух параллельно подключенных резисторов будет вычисляться по формуле:

                                                                                    R  R^{1 R2}                                          (2.53)

R1  R2 Сопротивление трех проводников:

                                                                             R  R1 R2 R3                                                                                              (2.54)

R1R2  R2R3  R1R3

 

Порядок выполнения работы задания 1

Задание 1. Проверить законы последовательного соединения проводников.

1.Собрать электрическую цепь по схеме (Рис. 2.17).  

 

 

Рисунок 2.17 − Схема электрической цепи

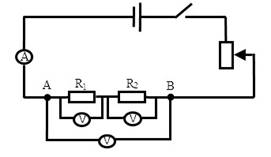
2. Снять показания вольтметра на резисторе R₁ и R₂, записать полученные напряжения U₁ и U₂, в таблицу 2.14.

3.Измерить полное напряжение U_АВ на участке АВ.

4.Измерить силу тока во всей цепи I_АВ, подключив амперметр последовательно, после или перед резисторами. 

5.Измерить силу тока I₁ и I₂ между резисторами R₁ и R₂. 

6. Внести полученные данные в таблицу 2.14.

 

Таблица 2.14 − Экспериментальные данные

 

Сопротивление [Ом]				Напряжение[В]				Сила тока[А]
R1	R2	R	U1	U2	U	UAB	I1	I2	I	IАВ

 

Обработка результатов измерения задания 1

 

1.Проверить соотношение силы тока по формуле (2.47).Сделать вывод. 

2.Рассчитать общее напряжение U на участке АВ по  формуле (2.48) и сравнить его с напряжением U_АВ, найденным экспериментально. Сделать вывод.

3.Определить общее сопротивление цепи R по формуле (2.49).

 

Порядок выполнения работы задания 2

 

Задание 2. Проверить законы параллельного соединения проводников.

1.Собрать электрическую цепь по схеме (Рис. 17).  

 

 

Рисунок 17 − Схема электрической цепи

 

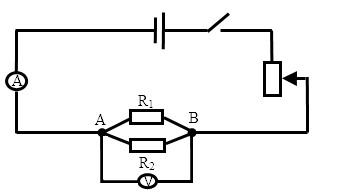
2. Снять показания вольтметра на резисторе R₁ и R₂, записать полученные напряжения U₁ и U₂, в таблицу 2.15.

3.Измерить полное напряжение U_АВ на участке АВ.

4.Измерить силу тока во всей цепи I_АВ, подключив амперметр последовательно, после или перед резисторами. 

5.Измерить силу тока I₁, подключив амперметр после или перед резистором  R₁ и I₂  – подключив амперметр после или перед резистором R₂.  6. Внести полученные данные в таблицу 2.15.

 

Таблица 2.15 − Экспериментальные данные

 

Сопротивление [Ом]				Напряжение[В]				Сила тока[А]
R1	R2	R	U1	U2	U	UAB	I1	I2	I	IАВ

 

Обработка результатов измерения задания 2

 

1. Рассчитать общее значение силы тока на участке АВ по формуле (2.50) и сравнить его с общим током I_АВ, найденным экспериментально. Сделать вывод.

2.Проверить соотношение напряжения по формуле (2.51). Сделать вывод.

3.Определить общее сопротивление цепи R по формуле (2.52 – 2.53).

 

Контрольные вопросы

 

1. Сформулируйте законы последовательного и параллельного соединения проводников.

2.Определите сопротивление участка цепи, изображенного на рисунке, между точками С и D, если R₁ = 2 Ом, R₂ =5 Ом, R₃ = 20 Ом, R₄ = 5 Ом, R₅ = 10 Ом

 

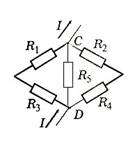
3.Найти полное сопротивление R показанной на рисунке цепи, если R₁ = R₂= R₅= R₆ = 3 Ом, R₄ = 24 Ом, R₃ = 20 Ом

 

        

4.            Найти сопротивление цепи, изображенной на рисунке, если каждое сопротивление равно 2 Ом.

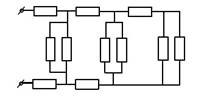
5.            Найдите распределения сил токов и напряжений в цепи, изображенной на рисунке, если вольтметр показывает 110 В, а R₁ = 6,4 Ом, R₂ =4 Ом, R₃ = 12 Ом, R₄ = 6 Ом, R₅ = 3 Ом, R₆ = 8 Ом, R₇ = 20 Ом.

 

Рекомендуемая литература

 

[1], [2], [3], [4], [5], [7]

 

2.8 Лабораторная работа №8

 

                   Тема:          Градуирование          термопары          и           определение

термоэлектродвижущей силы (термоэдс)

 

Цель: установить графическую зависимость электродвижущей силы термопары от различия температур ее спаев. Научиться работать с зеркальным гальванометром. Определить термоЭДС.

Оборудование: термопара константан – железо; два колориметра; один с холодной водой, другой с комнатной водой; горячая вода в сосуде; зеркальный гальванометр.

 

Краткие теоретические сведения

 

Термопара образуется при соединении друг с другом двух разнородных металлов. Место соединения обычно называется спаем. Между двумя соприкасающимися металлами возникает контактная разность потенциалов. Её возникновение связано с переходом свободных электронов из одного металла в другой, так как разные металлы имеют разную концентрацию электронов. В результате один металл заряжается положительно, другой – отрицательно. Это явление получило название термоэлектричества, а возникающая э.д.с. называется термоэлектродвижущей силой (термоэдс). Простейшую замкнутую цепь, состоящую из двух разнородных проводников (полупроводников) А и В (Рис.2.18), называют термоэлементом или термопарой.

 

                                                        Рисунок 2.18 − Термопара

 

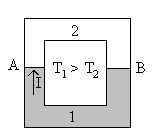
Возникновение термоэлектродвижущей силы в замкнутой электрической цепи, составленной из последовательно соединенных разнородных проводников, если места их контакта (спаи) поддерживают при различных температурах, называют явлением Зеебека.

Величина термоЭДС (ε) зависит от абсолютных значений температур спаев (T₁, T₂), разности этих температур ΔT и от природы материалов, составляющих термоэлемент. ТермоЭДС контура определяется формулой:

                                                                                         k T₂ T₁ k T                           (2.55)

где k – коэффициент термоЭДС; 

∆T-разность температур контактов, или

                                                                                           I  R  k T                                             (2.56)

Явление Зеебека, или термоэлектрический эффект, используют для измерения температур. Если один спай термопары поддерживать при постоянной температуре, а другой поместить в объем, температуру которого хотят измерить, то о величине температуры (согласно уравнению 2.56), можно судить по силе возникающего термотока, измеряемой гальванометром. Для этой цели необходимо сначала термопару проградуировать, т.е. установить соответствие между разностью температур спаев (t_n‑t₀) и показаниями гальванометра n. Из формулы 2.54 коэффициент термоЭДС термопары может быть определен по формуле

                                                                                                     k  I ^{ R}                                                                                                                    (2.57)

T

Зная k, можно легко измерить любые температуры по отклонению гальванометра, т.к. k показывает величину отклонения стрелки гальванометра при нагревании на 1 К

Величина тока I определяется по отклонению стрелки гальванометра, поэтому можно построить график зависимости между  различием температур и показаниями «зайчика»  гальванометра, тогда

n

                                                                                                             k                                             (2.58)

T

где n – величина показывающая число делений, на которые указывает «зайчик» гальванометра.

Установка (Рис.2.19) для выполнения работы состоит из железоконстантановой термопары, включенной в цепь по дифференциальной схеме, когда соединяются проводником одноименные металлы в, а измерительный прибор включается в ветвь металлов. Один из спаев помещается в калориметр с водой, находящейся при комнатной температуре, а другой  (нагреваемый спай) – в сосуд с водой, в которую будут постепенно добавлять горячую воду. В цепь включаются гальванометр. Температура фиксируется с помощью термометров T₁иT₂.

 

 

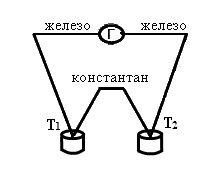
Рисунок 2.19. – Экспериментальная установка

 

Порядок выполнения работы 

 

Часть1

1.Соберите цепь с термопарой и зеркальным гальванометром (Рис.2.19). Установите «зайчик» на нулевой отметке шкалы.

2.Наполните 1-й колориметр водой и через несколько минут замеряйте температуру t₀.

3.Опустите оба конца термопары в колориметры. Во  второй колориметр наливайте по чуть-чуть горячую воду, каждую минуту замеряя температуру воды в нем.

4. Для каждого значения  температуры горячей воды во втором калориметре одновременно отмечайте показания «зайчика» гальванометра n.

5.Данные t_i и гальванометра n занесите в таблицу 2.16 сделав 10 замеров.

6.            На миллиметровой бумаге постройте график зависимости n(_∆t) показания «зайчика» гальванометра n и разности температур _∆t для горячей и холодной воды.

7.            По графику n(_∆t) прямой зависимости между n и _∆t определите k_ср – коэффициент термоЭДС. 8. Внесите данные в таблицу 2.16

         

Таблица 2.16 – Экспериментальные данные

 

№	Начальная температура t0 ,С0	Температура горячей воды tгор.С0	Показания амперметра n	Разность температур  t.С0	Среднее значение коэффициента термоЭДС k	термоЭДС ε, В
0
1
2
..

 

Часть 2

1.Не отключая зеркальный гальванометр и не меняя положения приборов, измерьте температуру горячей воды – это будет температура t₀ во второй части лабораторной работы. Снимите показания зайчика n0.

2. С помощью холодной воды, снижайте температуру воды во 2-м калориметре, ежеминутно снимая показания термометра в нем и показания «зайчика» гальванометра n.

3.Для каждого значения  температуры охлажденной  воды во втором калориметре одновременно отмечайте показания «зайчика» гальванометра n.

5.Данные t_i и гальванометра n занесите в таблицу 2.17 сделав 10 замеров.

6. На миллиметровой бумаге постройте график зависимости n(_∆t) показания «зайчика» гальванометра n и разности температур _∆t для холодной и охлажденной воды во 2-м калориметре.

7.По графику n(_∆t) прямой зависимости между n и _∆t определите k_ср – коэффициент термо ЭДС.

 

Таблица 2.17 – Экспериментальные данные

 

№	Начальная температура t0 ,С0	Температура охлажденной воды tхол.С0	Показания амперметра n	Разность температур  t.С0	Среднее значение коэффициента термоЭДС k	термоЭДС ε, В
0
1
2
..

 

Обработка результатов измерения

 

1.            2.Определить разность температур между значением горячей воды t_i⁰ и первоначальной t⁰. Внести полученные данные в таблицу 2.16.

∆t₁= t₁ – t₀

∆t₂= t₂ – t₀

………………..

∆t_i= t_i – t₀

2.            Определить         разность     температур          между         охлажденной         водой          и первоначальной. Внести данные в таблицу 2.17.

∆t₁= t₁ – t₀

∆t₂= t₂ – t₀

………………..

∆t_i= t_i – t₀

3.            Постройте графики зависимости n(_∆t) показания «зайчика» гальванометра n от  разности температур _∆t для горячей воды и отдельно для охлажденной воды.

4.            По графику n(_∆t) прямой зависимости между n и _∆t определите k_ср – коэффициент термоЭДС, учитывая, что

nñð

kñð 

t_ñð

5.Определите ЭДС термопары по формуле (2.55) для горячей и охлажденной воды, взяв одну и ту же разность температур.

6.Внесите все полученные данные в таблицу 2.16 и 2.17. Запишите вывод в работе.

 

Контрольные вопросы

 

1.  Что такое термопара? Из каких элементов она состоит?

2.  Какими причинами обусловлена контактная разность потенциалов?

3.  В чем состоит явление Зеебека?

4.  От чего зависит термоЭДС?

5.  Что значит проградуировать термопару?

6.  Для чего используют термопары?

 

Рекомендуемая литература

 

[1], [2], [3], [4], [5], [8]

         

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

 

Основная литература:

1.Андреева А.В., Кузина Л.А., Штрекерт О.Ю. Общая физика (основы физики): учебное пособие [Электронный ресурс] : учеб. пособие — Электрон. дан. — Вологда : ВоГУ, 2014. — 130 с. — Режим доступа: https://e.lanbook.com/book/93120

2.            Кузина Л.А.. Физика: курс лекций: в 3-х ч. Часть 1. Физические основы механики, молекулярная физика и термодинамика [Электронный ресурс] : учеб. пособие — Электрон. дан. — Вологда : ВоГУ, 2014. — 160 с. — Режим

доступа: https://e.lanbook.com/book/93121

3.            Кузина Л.А.. Физика: курс лекций: в 3-х ч. Часть 2. Электростатика, электрический ток, электромагнетизм [Электронный ресурс] : учеб. пособие — Электрон. дан. — Вологда : ВоГУ, 2014. — 140 с. — Режим доступа:

https://e.lanbook.com/book/93124

4.Дмитриева, В.Ф.Физика для профессий и специальностей технического профиля [Электронный ресурс] : учебник для учреждений сред.проф. образования / В.Ф. Дмитриева. - 7-е изд., стер. - М. : Академия, 2014. - 448 с.-.-

(Профессиональное образование). - Режим доступа: http://www.academiamoscow.ru/reader/?id=81671

5.Дмитриева, В.Ф.Физика для профессий и специальностей технического профиля [Электронный ресурс] : Лабораторный практикум : учеб.пособие для студ. учреждений сред. проф. образования / В.Ф. Дмитриева, А.В. Коржуев,

О.В. Муртазина. - М. : Академия, 2015. - 160 с. : ил.-.- (Профессиональное образование). - Режим доступа: http://www.academia-moscow.ru/reader/?id=81671

 

Дополнительные источники:

 

6.Самойленко  П.И.  Физика учебник для средних специальных заведений/ П.И Самойленко, - Ф.В.СергееваМосква «Академия»2014. - 321 с

7.Самойленко  П.И.  Физика учебник для средних специальных заведений/ П.И Самойленко, - Ф.В.СергееваМосква «Академия»2014. - 268 с

8.Трофимова Т.И. Курс физики с примерами решения задач в 2 т. Т. 1-2:

учебник/ Т.И. Трофимова, А.В. Фирсов. – М: КНОРУС, 2015.

 

Интернет-источники:

 

9.Министерство образования и науки РФ www.mon.gov.ru

10.   Российский образовательный портал www.edu.ru

11.   Департамент образования Тверской области www.edu.tvel.ru

12.Тверской областной институт усовершенствования www.tiuu.ru

                   13.Представление            опыта            работы,            класс             физика

physicam.ru>profskill/22/50.htm

        

Приложение А Методика определения погрешностей измерений

 

Выполнение лабораторных работ связано с измерениями физических величин. Измерения не дают возможности получить абсолютно точные результаты.         Погрешности       (ошибки),   возникающие      при    измерениях, объясняются несовершенством методов измерения, измерительных приборов, условиями опыта. Для исключения случайных ошибок и повышения степени точности необходимо производить всегда несколько измерений (минимум три), а затем найти среднее арифметическое.

Разность между истинным и измеренным значениями искомой величины называется абсолютной погрешностью Δх:

xxист х .

Отношение абсолютной погрешности к действительному значению измеренной величины называется относительной погрешностью измерения δ:

x

                     100%

xист

Если истинное значение искомой величины неизвестно, то для определения погрешностей можно воспользоваться методом среднего арифметического:

1.     Производят измерение искомой величины х несколько раз и среднее арифметическое результатов этих измерений принимают за истинное значение измеренной величины: x₁ x₂ x₃..x_n xср _хист n

2.     Находят абсолютные погрешности каждого измерения:

х₁ х₁ x_ср,

х₂ х₂ x_ср,

х₃ х₃ x_ср,

х_n х_n x_ср.

3.     Определяют среднее арифметическое этих погрешностей x₁ x₂ x₃..x_n xср n

и принимают его за абсолютную погрешность измерения.

4.     Находят относительную погрешность ε: x_ñð

             100%

x_ñð

        

Приложение Б Табличные данные

 

Таблица Б.1 −Плотность некоторых веществ

Жидкость	Плотность, 10 3кг/м3	Твердые тела	Плотность, 10 3кг/м3
Бензол	0,88	Алюминий	2,6
Вода	1,00	Железо	7,9
Глицерин	1,20	Латунь	8,4
Касторовое масло	0,90	Медь	8,6
Керосин	0,80	Олово	7,2
Ртуть	13,6	Свинец	11,3
		Сталь	7,7
		Пластмасса	1,004-1,008

 

Таблица Б.2−Коэффициент вязкости некоторых жидкостей

Жидкость	Коэффициент вязкостиη∙10 -6Па	Жидкость	Коэффициент вязкостиη∙106мкПа
Бензол	650	Масло касторовое	242 ∙104
Вода	1004	Масло машинное	240 ∙105
Глицерин	1499 ∙105	Масло подсолнечное	50 000
Керосин	1800-1900	Масло трансформаторное	19 800
Ртуть	1554

 

Таблица Б.3-Удельное электрическое сопротивление некоторых металлов, сплавов и материалов

Металл, сплав, материал	Удельное сопротивление   ρ,Ом∙м	Металл, сплав, материал	Удельное сопротивление ρ,Ом∙м
Алюминий	2,7 ∙ 10-8	Никелин	4,2∙10-7
Вольфрам	5,3∙10-8	Никель	7,3∙10-8
Дуралюмин	3,3∙10-8	Нихром	1,05∙10-6  -  1,1∙10-6
Железо	9,9∙10-8	Олово	1,13∙10-7
Инвар	81∙10-8	Осмий	9,5∙10-8
Иридий	5,3 ∙10-8	Реотан	4,5∙10-7
Константан	4,7∙10-7  -  5,2 ∙10-7	Сталь	1,2∙10-7
Калий	7,1∙10-8	Свинец	2,07∙10-7
Латунь	6,3∙10-8  -7,1 ∙10-8	Уголь	4∙10-5 - 5∙10-5
Магний	4,5 ∙ 10-8	Фехраль	1,1∙10-6 – 1,3∙10-6
Манганин	3,9∙10-7 – 4,8 ∙10-7	Цинк	5,95∙10-8
Медь	1,68 ∙10-8

Уколова Юлия Валериевна

 

 

 

 

 

 

 

 

Практикум по лабораторным работам

для студентов (курсантов) второго курса специальностей:

 

26.02.04 «Монтаж и техническое обслуживание судовых машин механизмов»

26.02.05 «Эксплуатация судовых энергетических установок»

26.02.06 «Эксплуатация судового электрооборудования и средств автоматики» 22.02.06 «Сварочное производство»

 

 

 

 

 

 

 

 

 

Судомеханический техникум ФГБОУ ВО «Керченский государственный морской технологический университет»

298309 г. Керчь, Орджоникидзе, 123