Практикум по построению интерполяционных многочленов.

Практикум по построению интерполяционных многочленов.

Задания для самостоятельного решения. V –  номер варианта.

I.                    Функция задана таблично

1.      Построить интерполяционный многочлен в форме Лагранжа и построить его график.

2.      Построить интерполяционный многочлен в форме Ньютона и построить его график.

II.                 Построить на отрезке [ 0, 1] многочлен наилучшего  среднеквадратичного приближения Ф₁(x)=C₀+C₁x для функции f(x)= sin²Vx .

Образцы решения задач.

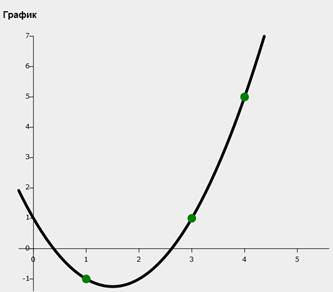
Задача №1. Функция задана таблично

1.      Построить интерполяционный многочлен в форме Лагранжа и построить его график.

Решение.

Интерполяционный многочлен Лагранжа для функции, заданной таблицей

имеет вид:

L_n =

У нас есть 3 точки, следовательно, степень полинома не больше, чем 2.

При помощи y координат составим запись полинома Лагранжа.

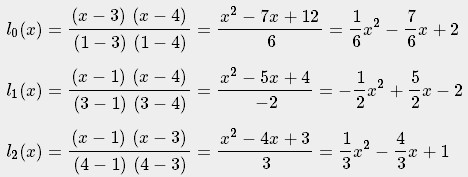
Подставляем базисные полиномы Лагранжа в формулу интерполяционного полинома и суммируем члены с одинаковыми степенными показателями.

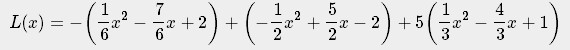
Ответ: L(x) = x²  3x 1

2.      Построить интерполяционный многочлен в форме Ньютона и построить его график.

Интерполяционный многочлен Ньютона, записанный для неравноотстоящих узлов:

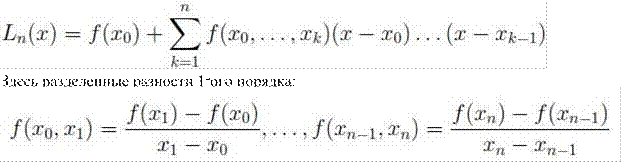
А разделенные разности k-ого порядка определяются через разделенные разности k-1-ого порядка:

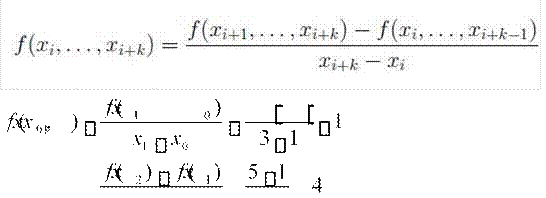                                                )  f x(       1 1

f x x( ₁, ₂)                               

                                            x₂  x₁                  4  3

f x x x( 0 1, , 2)  f x x( 1, 2)  f x x( 0 1, )  4 1 1

                                                            x₂  x₀                           4 1

L x     1 1 x 1  1 x 1x 3

Ответ: L(x) = x²  3 1x

Задача №2.  Построить на отрезке [ 0, 1] многочлен наилучшего  среднеквадратичного приближения Ф₁(x)=C₀+C₁x для функции f(x)=e^2x.

Решение.

Выберем шаг 0,1. Задаем функцию f(x)=e^2x  на отрезке [ 0, 1]  таблицей, выполняя расчеты средствами ЕXCEL:

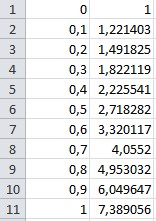
 По методу наименьших квадратов коэффициенты для функции Ф₁(x)=C₀+C₁x  могут быть найдены по формулам 

c1  n xi2 c0 n xi  n x yi      i

 i1                        i1              i1

         n                               n

 c1x c ni  0 yi                  

     i1                           i1

Используя ЕXCEL получаем таблицу:

        x          y               x²        xy

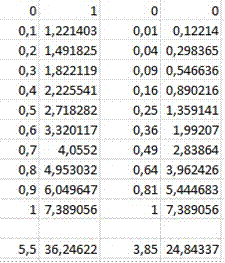
Суммы.

Решаем систему линейных уравнений:

c₁ 3,85 c₀ 5,5  24,84337

 c₁ 5,5 c₀ 11 36,24622

_

Отсюда  c₁=6,10933, c₀ =0,24045

Ф₁(x)= 6,10933x+0,24045

Этот результат можно получить, используя в ЕXCEL функцию ТЕНДЕНЦИЯ.

Графики данной и полученной функций:

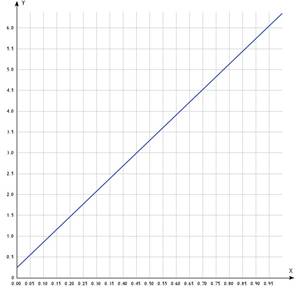
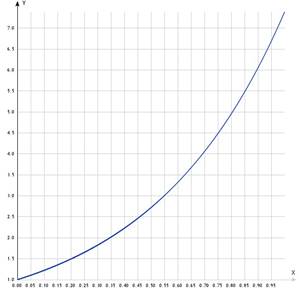
Ответ: Ф₁(x)= 6,10933x+0,24045 - многочлен наилучшего  среднеквадратичного

приближения для функции f(x)=e^2x