Правильные многоугольники, вычисление их элементов

Тема:  Правильные многоугольники, вычисление их элементов

2.Тип урока: Урок освоения новых знаний и умений

3.Планируемые результаты:

Предметные умения:

Распознавать геометрические фигуры на плоскости, определять их взаимное расположение, изображать геометрические фигуры

Личностные результаты:

Овладение основными навыками исследовательской деятельности, установка на осмысление опыта, наблюдений, поступков и стремление совершенствовать пути достижения индивидуального и коллективного благополучия

Ключевые слова: ЗАДАЧИ,МНОГОУГОЛЬНИКИ,ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ,ЭЛЕМЕНТЫ МНОГОУГОЛЬНИКОВ

Краткое описание:  На уроке предусмотрено использование следующих типов электронных образовательных материалов: «Галерея изображений (группа изображений по одной тематике)», «Самостоятельная работа».

                                Блочно-модульное описание урока

БЛОК1. Вхождение  в тему урока и создание условий для осознанного восприятия нового материала.

1.Мотивирование на учебную деятельность

Девиз урока:

Три пути ведут к знанию:

Путь размышления – это путь самый благородный;

Путь подражания – это путь самый легкий;

Путь опыта – это путь самый горький.  (Китайский философ и мудрец Конфуций)

2. Актуализация опорных знаний

Какие геометрические фигуры нами уже изучены?

Каковы их элементы?

Какая фигура называется многоугольником?

Виды многоугольников.

Что такое периметр многоугольника?

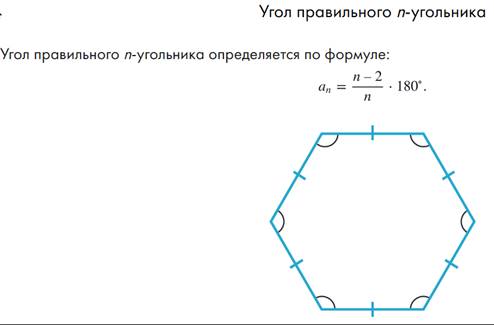
3. Целеполагание (Назовите цель: ты узнаешь, ты научишься……) сформировать  понятие  правильного  многоугольника.  Вывести   формулу  для  вычисления  угла  правильного  n - угольника  и  показать  ее  применение  в  процессе  решения  задач.

БЛОК 2. Освоение нового материала

1.Осуществление учебных действий по освоению нового материала

Среди множества различных геометрических фигур на плоскости выделяется большое семейство МНОГОУГОЛЬНИКОВ.

Названия геометрических фигур имеют вполне определенный смысл. Присмотритесь внимательно к слову «многоугольник», и скажите, из каких частей оно состоит. Слово «многоугольник» указывает на то, что у всех фигур этого семейства «много углов».

Подставьте в слово «многоугольник» вместо части «много» конкретное число, например 5. Вы получите ПЯТИУГОЛЬНИК. Или 6. Тогда – ШЕСТИУГОЛЬНИК. Заметьте, сколько углов, столько и сторон, поэтому эти фигуры вполне можно было бы назвать и многосторонниками.

При разборе примера 1 сказать, что данный факт справедлив для любого выпуклого многоугольника, не обязательно правильного. Провести аккуратное доказательство со всеми пояснениями и качественными чертежами в примере 2, поскольку данные чертежи и идеи будут использованы школьниками при самостоятельном доказательстве других формул этого урока.

Примеры 3 и 4 на использование формул и аккуратный подсчет, при этом результаты вычислений в общем виде в примере 3 можно рекомендовать школьникам к запоминанию.

Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

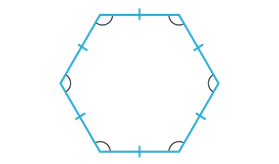
Примеры правильных многоугольников

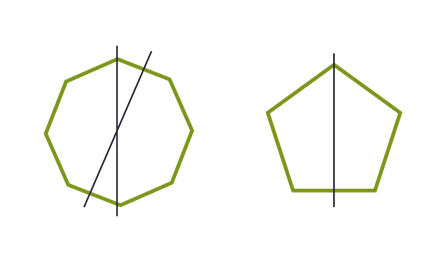
Симметрия правильных n-угольников

Правильный n-угольник имеет n осей симметрии.

n – чётно: оси проходят через противоположные вершины или через середины параллельных сторон, есть центр симметрии.

n – нечётно: оси проходят вершины перпендикулярно противолежащей стороне, нет центра симметрии.

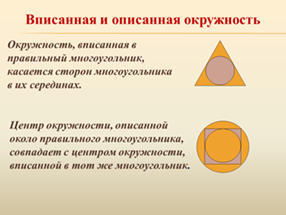
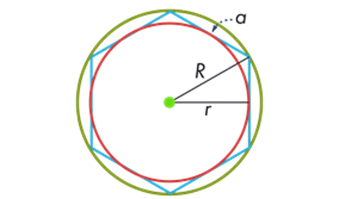
Описанная и вписанная окружности

Около любого правильного многоугольника можно описать окружность, и притом только одну.

В любой правильный многоугольник можно вписать окружность, и притом только одну.

Центры окружностей совпадают (центр правильного многоугольника).

БЛОК 3.  Применение изученного  материала

1.Применение знаний,  в том числе в новых ситуациях

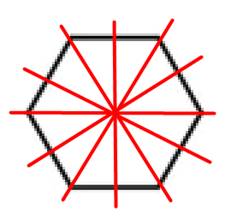
1.      Схематично изобразите правильный шестиугольник и проведите всего его оси симметрии. Сколько осей получилось? Имеет ли данный многоугольник центр симметрии?

Решение

О Изобразим правильный шестиугольник и проведём его оси симметрии. Всего шесть осей, причём три из них проходят через противоположные вершины, а три другие через середины параллельных сторон.

Оси симметрии пересекаются в центре правильного шестиугольника, и поскольку число вершин чётно, данная точка является центром симметрии.

2.Найдите угол при вершине октагона. Ответ дайте в градусах.

№ 1081 (в)

Дано: α – угол правильного             n – угольника

n = 6;

Найти: α        

Решение:

Ответ: α= 120°.

№ 1083 (в)

Дано: α – угол правильного             n - угольника

α = 135˚.

Найти: n

Решение:

,

,

,

,

,

,

,

Ответ: n = 8.

2.Выполнение межпредметных заданий из реальной жизни.

3.Задание ЕГЭ и ОГЭ

БЛОК 4. Подведение итогов, домашнее задание.

1. Рефлексия  (достигнуто или не достигнуто по образовательным результатам)

Обсуждаем итоги урока, выставляем оценки в журнал.

1.Что на уроке больше всего понравилось (запомнилось)?

2.Что было трудным?

3.Что так и осталось непонятным?

2. Домашнее задание.

Рекомендации по ДЗ.    №1087(3),№1091,1092

Скачано с www.znanio.ru