Правописание звонких и глухих согласных в корне. Способы проверки слов с парными согласными в корне

Задание 1

Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

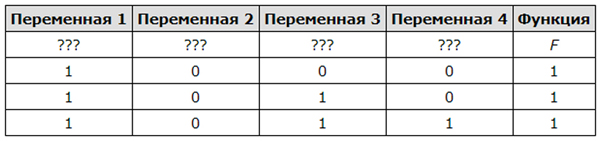
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Задание 2

Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

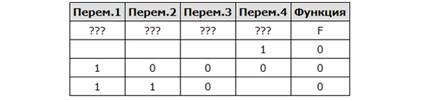
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Решение:
Задание1

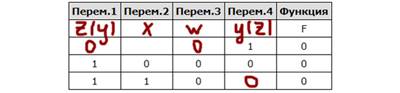
Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.

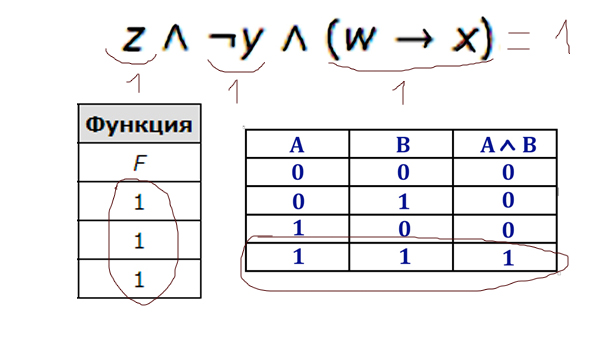
Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.

Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x - это третий столбец, а w - четвёртый.

Ответ: zyxw

Решение:
Определяем главную логическую операцию ("главную скрипку"), которая соединяет разные выражения. Видим, что это логическое сложение.

Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).

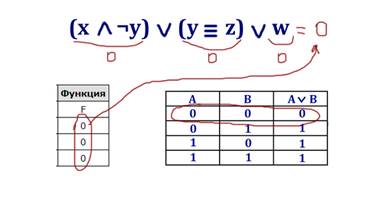
Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) - этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.

Следующим слабым звеном является равносильность. Она должна "выдавать" 0 (ноль). Равносильность "выдаёт" 0 (ноль), когда переменные разные!

Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).

Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).

Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.

Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x - 1 и ¬y - 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.

Тогда ответ будет равен yxwz.

Ответ: yxwz

Задача (Количество чисел)

Какое количество натуральных чисел удовлетворяет логическому условию:

¬(X² ≥ 9) ∨ ¬((X < 7) ∨ (X ≥ 10)) ?

Задача (Наибольшее число)

Для какого наибольшего целого неотрицательного числа A выражение

(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 205)

тождественно истинно, т.е. принимает значение 1 при любых целых положительных x и y ?

Задача (Наибольшее число + формула де Моргана)

Для какого наибольшего целого неотрицательного числа A выражение

(x < A) ∧ (y < A) ∧ (x * y > 603)

тождественно ложно, т.е. принимает значение 0 при любых целых положительных x и y ?

Задача (Наименьшее число)

Для какого наименьшего целого числа A формула

(3 * x + y < A) ∨ (x < y) ∨ (16 ≤ x)

тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y ?