Представление чисел в компьютере

Лабораторная № 4.

Представление чисел в компьютере.

Для работы с числами человек использует в основном две формы для их записи – естественная и экспоненциальная. Естественная форма:  1000 или 1,5. Экспоненциальная форма записи чисел обычно используется для обозначения очень больших или очень маленьких чисел, так как в естественной форме записи таких чисел используется большое количество незначащих нулей (например, 0,00000002 = 0,2´10 ).

Числа в компьютере представлены в двоичной системе счисления.

Кодирование целых чисел.

Запятая в таких числах фиксируется строго в конце и остается строго фиксированной. Поэтому этот формат называется форматом с фиксированной запятой.

Все целые числа в компьютере разделяются на числа без знака (только положительные) и со знаком (положительные и отрицательные). Для хранения чисел в памяти отводится определенное количество разрядов, в совокупности представляющих собой k-разрядную сеткуДля хранения целых неотрицательных чисел в памяти компьютера отводится 1 байт (8 битов) памяти.

Например: 10101010 ®

Для хранения целых чисел со знаком отводится 2 байта  (16 битов) памяти. Старший (левый) бит отводится под знак числа. Если число положительное, то этот бит равен 0, если число отрицательное, то бит равен 1.

Представление в компьютере положительных чисел в формате «знак-величина» называется прямым кодом. Чтобы записать прямой код числа, необходимо:

·        перевести число в двоичную систему счисления

·        заполнить ячейки k-разрядной сетки полученным числом, дополнив слева свободные ячейки нулями

Например:  2002  ®  11111010010  ® 

Для представления целых отрицательных чисел используется дополнительный код.

Алгоритм построения дополнительного кода.

1.     Модуль отрицательного целого числа записать прямым кодом для k-разрядной сетки.

2.     Получить обратный код числа. Для этого необходимо инвертировать (заменить все 0 -1-ми, а 1 – 0-ми) значения всех бит прямого кода.

3.     К полученному обратному коду прибавить 1. Получим дополнительный код.

Например: Записать дополнительный код числа -2002 для 16-разрядного представления с использованием алгоритма.

Замечание: дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие.

Пример: Выполнить арифметическое действие 3000 – 5000 (основание системы счисления 10) в 16-разрядном компьютерном представлении.

Алгоритм решения задачи.

·        представить число 3000 в прямом коде

·        представить число -5000 в дополнительном коде

·        сложить прямой код с дополнительным. Получим результат в дополнительном коде.

Чтобы сделать проверку правильности результата, переведем полученный дополнительный код в десятичное число.

Алгоритм перевода дополнительного кода в десятичное число:

·        инвертировать дополнительный код

·        прибавить к полученному коду 1 и получим модуль отрицательного числа

·        перевести результат в десятичное число и припишем знак отрицательного числа.

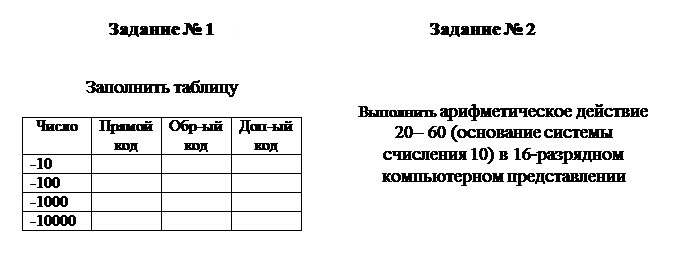
Недостатком представления чисел в формате с фиксированной запятой является конечный диапазон представления величин, недостаточный для решения математических, физических, экономических и др. задач, в которых используются как очень большие, так и очень малые числа.

Литература.

1.     Соколова, О.А. Поурочные разработки по информатике. М., ВАКО.- 2006. 400 с.

2.     Угринович, Н.Д. Информатика и информационные технологии. Учебник для 10-11 классов.-2-е изд. – М., БИНОМ. Лаборатория знаний, 2005. -511 с.

3.