Представление информации в различных системах счисления

Практическая работа №1

Тема: Представление информации в различных системах счисления

Цель:

- закрепление знаний о способах перевода чисел из одной системы счисления в другую;

 - формирование практических навыков перевода десятичных чисел в двоичную, восьмеричную, шестнадцатеричную системы счисления.

Вид работы: индивидуальный.

Время выполнения: 2 часа.

Теоретические сведения

Система счисления – это правило записи чисел с помощью заданного набора специальных знаков – цифр.

Система счисления (СС) – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита. Существующие СС можно разделить на позиционные и непозиционные. В непозиционных СС от положения цифр в записи числа не зависит величина, которую она обозначает.

Позиционную систему счисления называют традиционной, если её базис образуют члены геометрической прогрессии, а значения цифр есть целые неотрицательные числа.

В позиционных СС величина, обозначаемая цифрой в записи числа, зависит от её позиции. Количество используемых цифр называется основанием позиционной системы счисления.

Для записи чисел в позиционной системе с основанием n, нужно иметь алфавит из n цифр. Обычно для этого при n<10 используется n первых арабских цифр, а при n>10 к десяти арабским цифрам добавляют буквы.

Таблица 1 - Примеры алфавитов нескольких систем:

Основание системы, к которой относится число, приписывается нижним индексом к этому числу. Например: 101101₂  3671₈ 3B8F₁₆.

Таблица 2 - Таблица соответствия чисел между разными системами счисления

Двоично-шестнадцатеричная                   Двоично-восьмеричная

таблица                                                     таблица

Ход работы

1.                Для перевода смешанного дробного десятичного числа в любую другую систему счисления, необходимо:

a.                  целую часть числа делить на основание новой системы счисления до тех пор, пока частное (остаток от деления) не будет меньше основания новой системы счисления, они записываются снизу-вверх;

b.                 дробная часть числа умножается на основание новой системы счисления до полного её обнуления, или до получения нужного количества знаков в новом числе после запятой. Полученные цифры записываются сверху вниз.

Пример 1. Перевести десятичное число 315 в восьмеричную и в шестнадцатеричную систему:

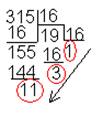
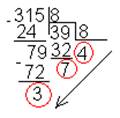
Отсюда следует: 315₁₀=473₈=13B₁₆.

Пример 2. Перевести десятичную дробь 0,1875 в двоичную, восьмеричную и шестнадцатеричную системы.

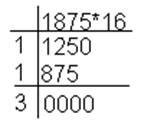
Здесь вертикальная черта отделяет части чисел от дробных частей. Отсюда: 0,1875₁₀=0,0011₂,=0,14₈=0,3₁₆.

2.     Для того чтобы произвольное двоичное число записать в системе счисления с основанием q=2ⁿ, нужно:

a.      данное двоичное число разбить слева и справа (целую и дробную части) на группы по n цифр в каждой (в 8-й СС n=3, в 16-й СС n=4);

b.     если в последних правой и левой группах окажется меньше n разрядов, то их надо дополнить справа и слева нулями до нужного числа разрядов;

c.      рассмотреть каждую группу как n- разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q=2.

Пример 3. Перевести смешанное число 1011101,10111₂ в восьмеричную систему.

Решение. Группы по три двоичных знака выделяются от запятой как влево, так и вправо. Затем производится перекодировка по таблице: 1011101,10111₂001 011 101,010 111₂135,27₈

Пример 4. Перевести шестнадцатеричное четное число 15FC в двоичную формулу.

Решение. Заменяем каждую цифру числа соответствующей группой чисел, получается: 0001010111111100. Если отбросить нули слева (в любой системе счисления они не влияют на значение целого числа), то получим искомое двоичное число. Таким образом: 15FC₁₆=0001010111111100₂ и наоборот, заменим каждую двоичную группу на соответствующую шестнадцатеричную цифру.

Задания к практической работе

Задание 1. Переведите смешанные десятичные дроби числа в двоичную, восьмеричную и шестнадцатеричную (поочередно) системы счисления оставив, пять знаков в дробной части числа.

1)    55,675;   3)  24,875;       5) 34,12;     7) 76,29;

2)    201,72;   4)  123,56;       6) 341,56;   8) 245,16.

Задание 2. Переведите смешанные двоичные числа в восьмеричную и шестнадцатеричную системы.

1)    100010,011101;             5) 101111,01100;

2)    1111000000,101;            6) 100000111,001110;

3)    101010,111001;             7) 101010,0010;

4)    100011,111;                   8) 1100011,11.

Задание 3. Переведите восьмеричные числа в двоичную систему счисления.

1)    256;     3)  24,025;       5)  657;          7) 0,344;

2)    0,345;  4)  0,25;           6)  76,025;     8) 345,77.

Задание 4. Переведите шестнадцатеричные числа в двоичную систему счисления.

1)    1AC7;  3)  2F,D8C;      5)  FACC;      7) FDA,12F;

2)    0,2D1; 4)  F0C,FF;      6)  0,FFD;      8) DDFF,A.

Задание 5. Переведите числа из шестнадцатеричной системы счисления в восьмеричную.

1)    A45;         3)                0,FDD5;        5) A24,F9;      7)      0,DFD3;

2)    24A,9F;    4)                F12,0457;      6) 54A;  8)      21D,567.

Задание 6. Переведите числа из восьмеричной системы счисления в шестнадцатеричную и десятичную:

1)    774;     3)  0,5432;       5)  665;          7) 0,7654;

2)    765,25; 4)  654,763;     6)  546,76;     8) 432,347.

Задание 7. Сравните смешанные двоичные числа в восьмеричной и шестнадцатеричной системе счисления:

1)    111111,101 и 110111,111;            5)      10110,1111 и 101011,101;

2)    110111,011 и 1110,10111;            6)      1110001,001 и 10001,11001;

3)    110111,1101 и 11110,1101;         7)      1111001,11001 и 1011101,11;

4)    110101,1011 и 10111,001;            8)      101011,01101 и 1111011,1001.

Контрольные вопросы и задания

1.     Какие системы счисления называют позиционными, а какие – непозиционными? Приведите примеры.

2.     Сколько цифр нужно для записи чисел в двенадцатеричной системе счисления?

3.     Предложите собственную классификацию систем счисления.

4.     Что называется основанием системы счисления?

5.     Почему для вычислительной техники особенно важна система счисления по основанию 2?

6.     Какие способы перевода целых десятичных чисел в двоичные и обратно Вы знаете?

7.     Как переводить смешанные числа из двоичного представления в восьмеричное представление и обратно?

8.     Переведите в десятичную систему счисления двоичные числа:

1₂;     101₂;           10000₂;       1000101010₂;       11001011₂.

9.     Какое из чисел больше: 5₁₀ или 10₅; 1000₂ или 10₈?

10. Как будет выглядеть в двоичной системе счисления десятичное число 0,125?

11.