Представление опыта работы по теме " Выявление уровня сформированности самоконтроля у младших школьников на уроках математики "

Способы формирование самоконтроля у младших школьников на уроках окружающего мира

    С целью выявление уровня сформированности самоконтроля у младших школьников на уроках математики была проведена опытно-экспериментальная работа. Базой исследования была МБОУ СОШ №24  3 «А» класс, в составе 22 учащихся. Дети обучаются по программе «Школа России».  Для определения уровня сформированности у учащихся самоконтроля была подобрана  методика: « Продолжи узор»  [31, с.37] Полученные результаты я распределила по уровням сформированности самоконтроля, выделенным и (6 уровней).По результатам диагностики и наблюдениям на уроках математики  за учениками  2 класса я сделала вывод, что низкий уровень самоконтроля у 14человек (70%). Средний уровень самоконтроля показали 5 человека(20%) ,  к высокому уровню близок только 3 человек(10%).

  Умение осуществлять самоконтроль развивается постепенно в процессе выполнения специально подобранных тренировочных заданий, обеспечивающих зрительное, слуховое, артикуляционное восприятие, понимание, запоминание учебного материала. Я подобрала совокупность заданий, способствующих формированию у младших школьников самоконтроля, все задания поделила  по сложности на 3 группы. Приведу в качестве примера некоторые задания.

  1 группа заданий. Задания на сверку с образцом.

Цель: формирование итогового самоконтроля.

Получить полный текст

Описание: Задания следует применять на начальном этапе обучения. При выполнении заданий ученики должны иметь возможность сверить свой результат с образцом. Эта проверка сначала должна проходить под руководством учителя: дети вместе с ним ищут соответствие между своим и готовым результатом, путем сравнения их и сопоставления. Чтобы навык устойчиво закрепился, нужно выделять специальное время на уроке для проверки своей работы, по образцу, пока большинство учащихся не начнут делать автоматически, без напоминания учителя. Образец проверки должен быть представлен в наглядном виде. Во время обучения учащихся этой деятельности учитель должен оценивать, прежде всего, как смог ученик сам проверить свою работу и исправить допущенные ошибки. К заданиям данного вида можно отнести и такие, в которых учитель сам делает установку на проверку результата. Для формирования итогового самоконтроля  мы применяли также на уроках математики задания  по работе с таблицами устного счета. Примеры заданий данной группы представлены ниже.

Задания на сверку готового результата с эталоном.

  При  самостоятельной работе на уроке ученики получают задание: найти значение выражения, решить задачу или уравнение. Затем учитель на доске или на слайде открывает готовое решение. Ученики сверяют полученные результаты, находят ошибки, исправляют.

а) Найдите значение выражения:

20+10

30-10

40+30

Сверьте свое решение с образцом на доске: 30, 20, 70.

б) Решите задачу:

На полке было 10 книг, а журналов на 5 больше. Сколько журналов было на полке?

Сверьте свое решение с образцом на слайде презентации.

  На этапе актуализации знаний учитель может использовать  работу с таблицами устного счета. Учащимся раздаются  таблицы со столбиками любых  примеров. Дается 2 минуты для решения. Учащиеся в тетрадь записывают только ответы. По истечении времени предлагаются ответы, учащиеся проверяют. После чего, каждый подсчитывает количество правильных ответов – баллов. Эти баллы записывают на обложку тетради. Так на протяжении нескольких уроков. Ученики контролируют и правильность выполнения задания, и отработку навыка.

Задания на проверку вычислений.

  В данных заданиях учитель сам делает установку на проверку результата. Такие задания можно использовать при выполнении самостоятельных или проверочных работ.

а) Найди значения числовых выражений, сделай проверку: 34+30, 67-20, 90-  70.

б) Реши уравнение и сделай проверку: х+54= 86, 57-у=13

  2 группа заданий. Задания  на пошаговый контроль.

Цель: Формирование пошагового контроля.

Описание: При обучении этому способу самоконтроля учащимся мы предлагали начать проверку работы не со сверки ответа, а с оценки правильности выполнения каждого этапа решения учебной задачи. На первых этапах работы по формированию этого вида  самоконтроля учащимся со средними и слабыми учебными возможностями должны иметь образцы алгоритмов для пошаговой проверки своей работы. Для уроков математики мы подобрали следующие виды данных заданий: круговые примеры, решение взаимообратных задач, решение задач разными способами, дидактические игры. Данные задания мы  использовали на основном этапе формирования самоконтроля. Правильность выполнения задания можно проверить, решив его другим способом. На примере конкретной задачи мы предлагали ученикам вспомнить, каким образом, решив задачу другим способом, можно узнать, правильно она была решена или нет. Умение находить разные способы решения задач формирует навыки самоконтроля.

  На данном этапе формирования самоконтроля мы предлагали также составить и решить задачи, обратные данной. Мы считаем, что если дети научатся и привыкнут работать с взаимообратными задачами, то постепенно они привыкнут контролировать решение прямой задачи, а значит, у них будет формироваться навык самоконтроля.

  В урок математики мы включали также  различные дидактические игры: «Цепочка»,  « Пазлы», «Мозаика». Они также способствуют формированию самоконтроля, так как прийти к  верному конечному результату в них можно только предварительно  выполнив цепочку промежуточных действий. Примеры заданий данной группы представлены ниже.

  На этапе актуализации знаний и подготовки к изучению нового материала можно использовать различные дидактические игры.

а) Реши круговые примеры. Круговые примеры составляются таким образом, что ответ каждого выражения являлся началом, какого - то другого и выполнить данное задание можно только осуществив пошаговый контроль. Такие задания эффективнее всего помещать на слайды презентаций.

8+3  13-3  9+3  12+1

  11-2  10-4  15-7  6+9

37-20  17-5  12+6  18-4  14+16  30+7

б) Игра «Цепочка». При выполнении вычислений ученикам необходимо контролировать каждый свой шаг, чтобы  получить верный  ответ.

27 - 7        +4 + 3 – 6 +5=26;

42 :  7 ∙3 : 3  ∙7 = 56.

в) Игра «Лесенка». Каждой паре детей дается одна карточка с примерами. Примеры составлены таким образом, что ответ одного является началом другого, задание дается в виде лесенки. Ответ каждого примера учащиеся записывают на соответствующей ступеньке. Каждый ученик может сам себя проконтролировать. Можно составить так примеры, что ответ каждого будет соответствовать номеру ступеньки, на которой он записан. Например, на первой ступеньке пример «5-4» и отсюда ответ на пример совпадает с номером ступеньки. Записывая ответ примера на каждой ступеньке, дети контролируют себя: по порядку ли они идут.

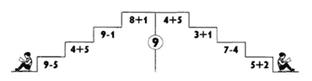
г) Игра «Мозаика». Это нехудожественная аппликация, а решение примеров. Заключается эта работа в следующем: берутся две карточки одинакового размера и расчерчиваются на одинаковые прямоугольники. На одной карточке пишутся примеры, а на другой, в соответствующих местах, ответы. На обратной стороне карточки с ответами наклеиваются забавные рисунки, и разрезается карточка по линии разметки. Получается таблица с примерами и отдельные карточки с ответами. Решая пример, ученик находит ответ и кладет его на место примера. Так заполняется вся таблица. Потом каждый ответ переворачивается, и если все примеры решены, верно, то получится рисунок.

д)  Игра « Математические пазлы», которые состоят из: а) поля с ответами, на котором собирается какое-либо изображение; б) пазлов с заданиями. Каждый ученик получает поле с ответами, на котором он будет собирать картинку, и набор пазлов, с одной стороны, которых изображен фрагмент картинки, а с другой - числовое выражение. Ученик должен вычислить значение выражения, найти этот ответ на поле и положить на него пазл изображением вверх. Если все вычисления выполнены правильно, то получится, например, иллюстрация к сказке «Теремок». Побеждает учащийся, справившийся с заданием первым.

е) Графические диктанты начинаются с начала 1 класса и продолжаются до конца учебного года: "Пёсик", "Буквы", "Человек", "Петушок", "Лодочка", "Цветок" и другие. Диктанты способствуют развитию внимания, собранности, самоконтроля. Конечным результатом у первоклассника должен стать рисунок на определённую тему, выполненный на клеточной основе – ребёнок видит свой результат (можно сравнить с заданным образцом у учителя – тогда это будет сличение с образцом).

Проведение графических диктантов дает возможность многоплановому развитию навыка самоконтроля учащихся в процессе их самостоятельной учебной деятельности: от побуждения к самоконтролю до его непосредственного формирования.

ж) Решение взаимообратных задач.

з) Решение заданий разными способами.

и) Тесты, с вариантами ответов.

  Тесты предоставляют учащимся возможность проявить самостоятельность, индивидуальность, способствуют обучению детей процессуальному самоконтролю. Большие возможности для этого представляют компьютерные тесты.

  3 группа заданий на прикидку результата.

Цель: формирование прогнозирующего самоконтроля.

Описание: Данные задания учат учащихся предвосхищать результаты еще не осуществленного действия. Эти задания мы использовали на заключительном этапе формирования самоконтроля. Учащиеся со слабыми учебными возможностями не могли с ними справиться, поэтому работали под руководством учителя.  Для формирования этого навыка мы учили учащихся способам прогнозирования результата без выполнения работы, для этого при выполнении задания они сначала с помощью учителя, а потом самостоятельно отвечали на вопросы:

•        Что нужно для решения проблемы;

•        Каким способом её можно решить;

•        Достаточно ли у них знаний для выбранного способа;

•        В каком виде должен быть представлен результат.

Примеры заданий данной группы представлены ниже.

а) Задания с недостающими, лишними данными.

б) Исправь ошибки.

Такие задания целесообразно вводить на этапе отработки навыка решения задач и нахождения значений выражений.

а)  Исправьте ошибки в условиях  и решите задачи:

Ваня и Петя играли в шахматы. Ваня выиграл 20 партий, а Петя на 5 партий меньше. Сколько партий выиграл Ваня?

б) У Дуремара 18 пиявок. Он разместил их в банки поровну. Сколько пиявок в одной банке?

в)  Проверь правильность вычислений. Исправь ошибки:

84+2 – 40=46, 62 – 7-9=46, 6+34 – 7=30.

  Задания на прикидку результатов.

а) «Магические квадраты»

Ученики при выполнении задания должны поместить цифры о 0 до 8 таким образом, чтобы сумма вдоль  каждой строки квадрата была равна 15.

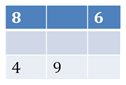
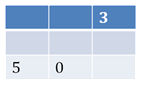
  Выполняя задания данного вида, ученики должны заранее продумывать, подбирать вместо звездочек нужные числа. Такую работу можно проводить на этапе закрепления и отработки вычислительных навыков.

  397  470  * ∙ 6 = 48

+*49  _**9  72:  *=9

  -----  -----

  9**  *41

Восстанови пропущенные знаки действий.

8  * 7  *  5=10  14 *  10 *  6=10

8  *  7 *  5=6  12  *  2 *  8=18

Спиши, расставляя, где нужно, скобки так, чтобы равенства стали верными.

25 – 20-4=1  18-6+4=8

15 – 6+8=17  30-3+5=22

Данные упражнения мы выполняли в классе на уроках математики в течение полугодия. Для повторной диагностики детей я использовали методику «Кодирование»(ll-ый субтест теста Д. Векслера в версии ).

  Результаты, полученные на контрольном этапе работы, свидетельствуют о положительной динамике в формировании самоконтроля у второклассников на уроках математики.2(20%)ученика имели все еще недостаточный уровень самоконтроля. Но у 6 (60%)был выявлен средний уровень, а у двух учеников (20%) – высокий уровень самоконтроля.

  Таким образом, моя  цель достигнута, гипотеза подтвердилась. Данные задания учителя начальных классов могут использовать на уроках математики для формирования самоконтроля.

Список литературы.

Ануфриев, А. Ф., Костромина, преодолеть трудности в обучении детей. Психодиагностические таблицы. Психодиагностические методики. Коррекционные упражнения. – 3-е изд., перераб. и доп./ , .- М.: изд-во «Ось-89», 2005. -272 с.

Асмолов, А. Г.  Виды универсальных учебных действий. Как проектировать учебные действия в начальной школе. От действия к мысли/ . М.: Просвещение, 2010.- 150 с.

Сластенин, педагогика: Учеб. пособие для студ. Высших учебных заведений в 2 ч. / . – М.: Гуманит изд-во. Владос.- 2003. – Ч. 1. – 288 с. Федеральный государственный образовательный стандарт начального общего образования второго поколения. М.: Просвещение.- 2009.-21 с.

Эльконин, в психологию развития/ .- М.: Педагогика. - 2001.-36

Скачано с www.znanio.ru