Преобразование алгебраических и рациональных степенных выражений. Преобразование иррациональных степенных выражений.

Лекция №8

Тема: Преобразование алгебраических и рациональных степенных выражений. Преобразование иррациональных степенных выражений.

Количество часов: 2 часа

Цель: обобщить и систематизировать знания о преобразовании алгебраических выражений; отработать практические навыки обучающихся по преобразованию алгебраических выражений, обобщить и систематизировать знания о рациональных и иррациональных выражениях.

План:

1.       Общие сведения об алгебраических выражениях.

2.       Типовые примеры преобразования алгебраических выражений.

3.       Общие сведения о рациональных выражениях.

4.       Общие сведения об иррациональных выражениях.

5.       Типовые примеры решений.

6.       Практическая часть.

Вопрос 1. Общие сведения об алгебраических выражениях.

Алгебраическим выражением называется выражение, в котором числа и буквы соединены действиями сложения, вычитания, умножения, деления, возведения в степень или извлечения арифметического корня.

Равенство, обе части которого принимают одинаковые числовые значения при любых допустимых значениях входящих в него букв, называется тождеством.

Например, каждая из формул сокращенного умножения представляет собой тождество, ибо левая и правая части каждого из равенств:

При выполнении тождественных преобразований алгебраических выражений необходимо знать порядок выполнения действий, действия с дробями и степенными выражениями, формулы сокращенного умножения и др.

При тождественных преобразованиях остаются неизменными:

1) величина допустимых изменений буквенных величин;

2) область допустимых значений каждой из буквенных величин.

Первое из этих требований является обязательным при всех преобразованиях, имеющих целью упрощение выражения или приведение его к нужному виду.

Например: Дополнить квадратный трехчленх² + 6х – 7 до полного квадрата.

Решение: прибавим к данному квадратному трехчлену число 9, и такое же число вычтем, т.е.:х² + 6х – 7 + 9 – 9 = (х + 3)² - 16

Вопрос 2. Типовые примеры преобразования алгебраических выражений.

Пример 1.

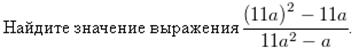
Пример 2.

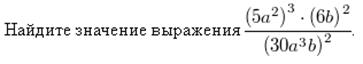
Пример 3.

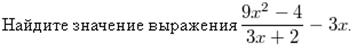
Пример 4.

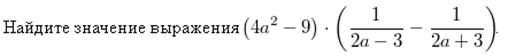
Пример 5.

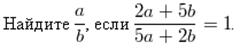
Пример 6.

Вопрос 3. Общие сведения о рациональных выражениях

Любое дробное выражение можно записать в виде , гдеPи Q– рациональные выражения, причем Qобязательно содержит переменные. Такую дробь  называют рациональной дробью.

Примеры рациональных дробей:

,     ,    

Основное свойство дроби выражается тождеством , справедливым при условиях  и ; здесь R – целое рациональное выражение. Это значит, что числитель и знаменатель рациональной дроби можно умножить или разделить на одно и то же отличное от нуля число, одночлен или многочлен.

Дробно-рациональные выражения, содержащие переменную под корнем, упрощаются с помощью двух шагового алгоритма:

1.     Раскладываем знаменатели всех дробей на множители, в т.ч. используя формулы сокращенного умножения:

2.     Приводим все дроби к общему знаменателю, а затем находим подобные слагаемые в числителе.

Вопрос 4. Типовые примеры решений

Вопрос 5. Практическая часть

Вопросы для самопроверки:

1.     Дайте понятие алгебраическому выражению.

2.     Какие формулы сокращенного умножения вы знаете?

3.     Какое выражение называется рациональным?

4.     Как выполняется упрощение дробно-рациональных выражений?

5.     Перечислите формулы сокращенного умножения.

Список литературы и ссылки на Интернет-ресурсы, содержащие информацию по теме:

1.      Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.  Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 431 с.: ил.

2.      Выгодский М.Я. Справочник по элементарной математике / М.Я. Выгодский. – М: Книга по требованию, 2013.-513с.

3.      Материалы по математике Материалы в Единой коллекции цифровых образовательных ресурсов: http://school_collection.edu.ru/collection/matematika/

4. Вся элементарная математика: Средняя математическая интернет – школа http://www.bymath.net

Скачано с www.znanio.ru