Поделиться
Л2-002038.docx
Преобразования из десятичной системы счисления в любую другую систему
Преобразование выполняется отдельно для целой и дробной части числа. Все операции выполняются по правилам десятичной арифметики. Основание новой системы рассматривается как десятичное число.
Преобразование целой части выполняется путем последовательного деления целой части на основание новой системы. На каждом шаге вы- числяется целая часть и остаток от деления. Остатки и есть значение цифр числа в новой системе счисления. Полученные остатки записыва- ются в новой системе счисления. На первом шаге будет получена млад- шая цифра. Процесс продолжается, пока очередная целая часть не ока- жется меньше основания новой системы счисления. Эта целая часть есть старшая цифра числа.
Правила перевода следуют из формы записи числа в позиционной системе счисления:
Шаг 1 A10 = an-1Sn-1+…+a1S1+ a0 | :S Þ an-1Sn-2 +…+ a1S0 +
a0 ® a0
Целая часть Остаток
Шаг 2 A10 = an-1Sn-2+…+a2S1+
a1 | : S Þ an-1Sn-3 +…+ a2S0 +
a1 ® a1
S
Целая часть Остаток
Шаг n-1 A10 = an-1S1+ an-2 | : S Þ an-1 +
an-2 ® an-2
Целая часть Остаток
Пример: 23[10] ® ?[2] Пример: 23[10] ® ?[8] Пример: 23[10] ® ?[16]
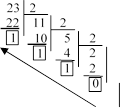
старшинство цифр
старшинство цифр
старшинство цифр
10111[2] 27[8] 17[16]
Преобразование дробной части выполняется путем последовательного умножения дробной части на основание новой системы. На каждом шаге выделяется новая целая часть и новая дробная часть. Последователь- ность целых частей дает значение цифр числа в новой системе счисле- ния. На первом шаге будет получена старшая цифра дробной части в но- вой системе. Процесс продолжается до получения заданного количества значащих цифр или нулевого значения дробной части.
 |
|||
 |
|||
Правила перевода следуют из формы записи числа в
позиционной системе счисления: Шаг 1 A10
= a-1S-1 + a-2S-2 +…+a-mS-m
| * S Þ a-1 + a-2S-1 + … +a-mS-m+1
Целая часть Дробная часть Шаг 2 A10 = a-2S-1 +…+a-mS-m+1 | * S Þ a-2 + a-3S-1 + … +a-mS-m+2
Пример: 0.125[10]®?[2]
Целая часть Дробная часть
В данном примере преобразование завершено при получении нулевой дробной части.
0.125[10]®0.001[2]
Пример: 0.55[10]®?[16]
В данном примере преобразование проводится до получения трех значащих цифр дробной части.
0.55[10]®0.8СС[16]
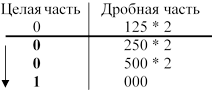Целая часть
0
8
C C
Дробная часть
55 * 16
800 *16
800 *16
800
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
