«Преодоление информационных барьеров восприятия математики в ходе познавательной активности школьников».

ИНСТИТУТ УСОВЕРШЕНСТВОВАНИЯ УЧИТЕЛЕЙ

 

 

                                  

 

 

 

 

 

 

педагогическоЕ исследованиЕ на тему:

 

 

«Преодоление информационных барьеров восприятия математики в ходе познавательной активности школьников».

 

 

 

 

 

 

 

 

                                                                Выполнила:  Тряпочкина Е.Н.

 

 

 

 

 

 

 

 

 

 

 

 

 

П. Спирово

2020 год

Содержание:

 

Цель  -------------------------------------------------------------------------------        3

Введение  --------------------------------------------------------------------------       5

1.     Языковой барьер ---------------------------------------------------------       6

2.     Знаковый барьер ---------------------------------------------------------       8

3.     Ситуативный барьер ----------------------------------------------------       9

4.     Ситуативный барьер  ----------------------------------------------------      14

5.     Познавательная активность школьников  ---------------------------     15

6.     Принципы развивающего обучения  ----------------------------------     18

7.     Результативность ----------------------------------------------------------     23

Заключение  ------------------------------------------------------------------------     24

Список литературы ---------------------------------------------------------------     26

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Противоречия.

 

1.                     Большой объём информации и неумение подвести решаемую задачу под нужное понятие (правило, формулу).

2.                     Социальные проблемы общества и отсутствие чёткой мотивации на учебную деятельность.

Проблема:

 

Известно, что математика – меганаука. Это язык международного общения, её методами пользуются все науки, именно поэтому перед учителями математики стоит очень важная проблема – научить детей использовать математику для того, чтобы лучше усваивались другие предметы школьного курса.

Тема:

«Преодоление информационных барьеров восприятия математики в ходе познавательной активности школьников».

Актуальность:

Исследование может быть использовано для работы в любом классе учителем любого предмета. Применение ИКТ делает его не только актуальным, но и современным.

Объект исследования:

Обучающийся. Учитель.

Предмет:

Математика.

Цель:

Выявить информационные барьеры и научить обучающихся  преодолевать их в ходе познавательной деятельности.

Задачи:

n  Формирование и дальнейшее развитие мыслительных операций: анализа, сравнения, обобщения и т. д.

n  Развитие логического и творческого мышления.

n  Воспитание интереса к  предмету, деятельности.

n  Развитие качеств творческой личности, таких, как познавательная активность, упорство в достижении цели, самостоятельность.

Гипотеза:

Научившись математике, дети лучше будут усваивать и другие предметы школьного курса.

Значение для практики:

n  Дети будут любить математику и с нетерпением ждать новых удивительных открытий.

n  Запоминать яркие картинки, а вместе с тем и формулы.

n  Использовать компьютер для приготовления уроков.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение.

Обучение - это приобретение новых знаний, умений и навыков. Сведения, которые являются для человека новыми, называются информацией. Информация поступает из различных источников: это учебники, художественная литература, различные СМИ, общение с педагогами, с друзьями, с природой и многое, многое другое. В последнее время информации так много, что человек, тем более ребёнок, не может определить нужность и важность получаемых сведений.

Обучение считается успешным, если необходимая информация осознанно интересует обучающегося, тогда она усваивается, превращаясь сначала в знание, а затем отрабатывается, становясь умением, и в результате становится навыком. При этом обучающийся является объектом обучения, т.е. сам старается приобрести необходимые знания. Но на практике, к сожалению, так случается не всегда. Существуют информационные барьеры, препятствующие приобретению прочных знаний. Их, на мой взгляд,  можно классифицировать следующим образом:

> языковой барьер;

> знаковый барьер;

> ситуативный барьер;

> барьер внутреннего несогласия.

Естественно, большинство из них  возникает при получении и усвоении любой информации, не только учебной и не только по математике. Но  целью данной работы является изучение барьеров, возникающих при освоении курса математики, и методов их преодоления.

 

 

 

 

 

 

I. Языковой барьер

Никто не будет спорить, что математика является одним из самых сложных предметов школьного курса. Основная задача математики - развитие мышления. Мыслить - значит уметь анализировать, выявлять логическую структуру понятия, сравнивать, соединять отдельные части в целое, проводить индуктивные и дедуктивные методы доказательства. Однако некоторые учащиеся не овладевают приёмами мышления даже к 10, 11 классу, а это приводит к тому, что не происходит полноценного усвоения материала. У многих возникает ситуация - определение запомнил «вызубрил», а работать с ним не научился. Кроме того, нередко дети, оканчивающие начальную школу, не умеют учить правила т.к. программы (такие, например, как математика по Л.Г. Петерсон или по Б.П. Гейдману) не предполагают заучивания, ставка делается больше на логическое мышление, фантазию, меньше - на запоминание. Но любая наука, и математика не является исключением, изобилует терминами, а как можно делать какие-либо мыслительные операции над понятием, не зная, что это понятие означает. Вот тут-то и появляется первый информационный барьер - языковой.

Для преодоления языкового барьера учащемуся необходимо знать значение каждого термина, используемого в рамках изучаемого предмета, для этого необходимо грамотно подвести ребёнка к понятию и тщательно его отработать. Привести примеры, контрпримеры, и только когда изучаемое понятие станет очевидным для каждого, его можно использовать для более сложных умозаключений: для решения примеров и задач, для составления алгоритмов, и т.д.

Приведу простейший пример. Учащемуся требуется решить уравнение и сразу возникает масса вопросов: что такое уравнение? что значит решить уравнение? какое это уравнение? (от этого зависит, каким методом его решать). Именно поэтому, после изучения нескольких видов уравнений, необходимо проводить сравнительный анализ уравнений и способов их решения. Сразу после изучения нового вида уравнения, необходимо определить, чем оно отличается от ранее изученных. На уроках повторения при подготовке к экзаменам желательно посмотреть на различные уравнения,  сравнить их, найти все сходства и отличия, повторить способы их решения. Если одно уравнение можно решить несколькими способами, то обучающийся вправе выбрать любой из них, наиболее удобный именно для него.

Особое место занимает, работа над определениями при изучении геометрии, когда необходимо сформировать базу, для дальнейшего усвоения этой сложнейшей и важнейшей науки. Любая геометрическая задача требует от ребёнка определённых знаний. Простейший пример, решим задачу: «Средняя линия трапеции равна 8 см, а одно из оснований равно 6 см. Чему равно другое основание?» И масса вопросов. Как решить задачу, не зная, что такое трапеция? Основание трапеции? Почему оснований два? Что такое средняя линия трапеции? Поэтому, для успешного изучения необходимо заставить обучающегося быть непосредственным участником «открытия» нового определения. Придумать такую ситуацию, в которой он сам даст нужное определение. Так при введении определения треугольника провести, например, практическую работу: «Построить три точки, не лежащие на одной прямой, соединить их попарно отрезками». Как, по-вашему, называется эта фигура? (Треугольник). Дайте определение треугольника! Как правило, всегда находится несколько человек в классе, дающих правильное определение сразу, с остальными мы находим его в учебнике, читаем несколько раз. На следующем уроке – надо обязательно спросить определение. После такой работы для всех очевидно, что такое треугольник. (Приложение 1)   

 

 

 

 

 

II. Знаковый барьер.

Любая точная наука, как известно, изобилует формулами. Незнание формул - это не что иное, как знаковый барьер, который также необходимо преодолеть для успешного усвоения, в частности математики. Если учащийся не знает формулы для вычисления длины окружности, то, как он найдет её длину, а если он не знает формулу площади, то, как он решит, например, задачу, которую предлагают на экзаменах выпускникам основной школы: «Длина садового участка на 10 метров больше его ширины. Его площадь решили увеличить на 400 м². для этого длину увеличили на 10м, а ширину - на 2 м. найдите площадь нового участка». Поэтому,  прежде чем учить решать ту или иную задачу, выполнять то или иное задание, необходимо, чтобы каждый учащийся понимал, о чём идёт речь, знал формулу, умел распознать её среди множества других, знал значение каждой буквы, входящей в неё, иначе все попытки успешного усвоения материала будут тщетны. Как же добиться того, чтобы «набор значков» был понятен? Может быть попробовать вывести эту формулу вместе с детьми? Именно тот факт, что ребёнок САМ получил требуемый результат и есть гарантия того, что он запомнит это надолго.

(Приложение 2)   

 

 

 

 

 

 

 

 

 

 

 

III. Ситуативный барьер.

В наше время, время прогресса информации так много, что трудно охватить весь её объём, за тот промежуток времени, который определен рамками урока. Т.е. времени на уроке просто не хватает. Кроме того, дети часто не понимают в школе того, что понадобится их потом. И тут возникает ситуативный барьер, который также препятствует успешному усвоению материала, а значит развитию личности. Поможет преодолеть этот барьер структурирование материала:

- чётко изложить цель;

- отработать минимум фактов, подтверждающий данный вывод;

- выстроить материал в логике безвариантного доказательства, оформить его в таблицу или презентацию. Все эти меры помогут сэкономить время. Незаменимым помощником в преодолении ситуативного барьера служит компьютер.  С появлением примеров компьютерного обучения к созданию компьютерных обучающих программ приобщились десятки тысяч педагогов - специалистов в различных областях знания, чаще всего в технических науках. В разрабатываемых ими программах, опираясь в основном на интуицию и практический опыт, они воплощали свои представления о преподавании конкретных дисциплин с помощью компьютеров.

Благодаря своим конструктивным и функциональным особенностям современ­ный персональный компьютер является уникальной по своим возможностям обучающей машиной. Он находит применение в обучении самым разнообразным дисциплинам и служит базой для создания большого числа новых информационных технологий обучения. Какие же особенности персонального компьютера так выгодно отличают его от прежде известных обучающих машин и технических  средств обучения?

Технические возможности персонального компьютера, если компьютер используется как обучающее средство, позволяют

·     активизировать учебный процесс;

·     индивидуализировать обучение;

·     повысить наглядность в предъявлении материала;

·     сместить акценты от теоретических знаний к практическим;

·     повысить интерес учеников к обучению.

Активизация обучения связана с диалоговым характером работы компьютера и с тем, что каждый ученик работает за своим компьютером или работают вместе, если в классе есть проектор или интерактивная доска. При традиционном классном обучении основное - это восприятие учащимися информации в устной форме, при этом ученику не часто приходится проявлять активность на уроке, и учитель не в состоянии организовать и контролировать активную работу каждого ученика на его рабочем месте. Поэтому традиционное обучение, в основном, является пассивным - многие педагоги сетуют, что на уроке, активно работают 20 – 30% учащихся. Если же обучение ведется в компьютерном классе, компьютер диалоговым характером своей работы стимулирует ученика к деятельности и контролирует ее результаты.

Индивидуализация обучения при использовании компьютера также связана с интерактивным характером работы с компьютером и наличием компьютеров на рабочих местах: каждый ученик теперь может сам выбирать темп обучения, делать в работе паузы. Более глубокий и тонкий учет индивидуальных особенностей уча­щихся может осуществлять компьютерная программа, с помощью которой ведется обучение (педагогическое программное средство, сокращенно ППС). С помощью начального теста программа может определить уровень обученности ученика, и в соответствии с этим уровнем предъявлять теоретический материал, вопросы и задачи, а также подсказки и помощь. Обучение слабых учеников программа ведет на самом легком (базовом) уровне, изложение теоретических сведений максимально упрощено, вопросы и задачи облегчены, помощь имеет характер прямой подсказки. Обучение сильных учеников ведется на наиболее сложном уровне, теория излагает­ся углубленно, предлагаются творческие задачи, требующие изобретательности и интуиции, а помощь имеет косвенный характер - намека или наводящего на пра­вильный путь соображения. Между этими крайними случаями обучающая про­грамма может учитывать более тонкую градацию подготовленности учащихся.

Каждый ученик в процессе обучения сталкивается с трудностями индивидуального характера, связанными с наличием пробелов в знаниях или особенностями мышления. При обучении с помощью компьютера обучающая программа может диагностировать пробелы в знаниях ученика, его индивидуальные особенности и строить обучение в соответствии с ними.

Графические возможности дисплеев персональных компьютеров и гибкие языки программирования позволяют сделать компьютерное обучение очень наглядным. В самом деле, теперь на каждом рабочем месте ученика имеется телевизор - дис­плей, на экране которого с помощью языка программирования можно без всякой кино- и видеосъемки показывать геометрические фигуры и построения, стилизо­ванные изображения реальных объектов и т.п. - и все это как статически (т.е. неподвижно), так и динамически, в движении. С помощью компьютерной графики можно сделать зримыми или, как еще говорят, визуализировать такие явления и процессы, которые не могут быть увидены в действительности (тем более в услови­ях школьного класса), можно создать наглядный образ того, что на самом деле никакой наглядности не имеет (например, эффектов теории относительности, закономерностей числовых рядов и т.п.). На этой возможности компьютеров основывается, так называемая, когнитивная компьютерная графика - особое направление применения компьютеров в научных исследованиях, когда иллюстра­тивные возможности компьютера используются для изучения различных законо­мерностей.

Всегда остро стоит вопрос о соотношении теории и практики применительно к научному знанию, обучению и т.д. (на это обращал внимание еще гётевский Мефи­стофель: «Суха теория, мой друг, но древо жизни вечно зеленеет»). Традиционное обучение является преимущественно теоретическим. Классно-урочная форма обучения исподволь, незаметно подталкивает каждого педагога в отдельности и всю систему образования в целом к усилению теоретической стороны обучения в ущерб практической. В самом деле, любому педагогу излагать теоретические знания у доски и требовать от учеников воспроизведения этого изложения значительно легче, чем организовывать ориентированную на практику работу учащихся. Если же вести обучение с помощью компьютера, оно приобретает практический уклон: диалоговый характер работы с компьютером, его вычислительные моделирующие возможности предрасполагают к обучению в форме решения задач (и к тому же задач практической направленности).

Важным условием успешного обучения является интерес учеников и изучаемому предмету, ходу обучения и его результату. Этот интерес связан с множеством факторов: содержанием изучаемого предмета, уровнем его сложности, организацией процесса обучения, системой поощрений и наказаний, применяемой учителем, личностными качествами самого учителя (его мастерством и интересом к предмету), системой ценностей ученика, его ближайшего окружения, родителей, взаимоотно­шениями в классном коллективе, социальным заказом в подготовке по направле­нию науки, представляемому данным предметом. В последнее десятилетие действует очень настоятельный социальный заказ в отношении всего, что связано с компью­терами (в подготовке специалистов по компьютерам и их применению, в развитии компьютерных технологий, в распространении компьютерной грамотности - умению использовать компьютер для решения разнообразных прикладных задач в различных сферах профессиональной деятельности).

Действию скрытого социального заказа мы обязаны появлением большого числа «компьютерных» талантов и дарований. Сфера деятельности, связанная с компьюте­ром, непосредственная работа на компьютере сама по себе обладает привлекательны­ми чертами, втягивает в себя людей. Существует даже особая категория людей («хакеров»), увлекшихся сложными и тонкими вопросами управления компьюте­рами, программированием различных компьютерных эффектов. В некоторых случаях можно говорить даже о возникновении психологической зависимости человека от компьютера – настолько велико мотивирующее влияние компьютера.

Компьютерная технология повышает интерес к обучению предметам, не связан­ным с информатикой. Новое в организации учебного процесса с участием компьютера, само изменение характера работы ученика на уроке способствуют повыше­нию интереса к учебе. В то же время, более тонкое использование возможностей компьютера позволяет управлять мотивацией учеников во время компьютерного обучения. Здесь имеются в виду, в первую очередь, мотивирующие реплики обу­чающих программ, т.е. фразы, в которых обучающая программа оценивает работу ученика и стимулирует дальнейшее обучение. Эти фразы могут иметь неформаль­ный характер с оттенком юмора и создавать теплую партнерскую эмоциональную атмосферу при работе с компьютером. Большое значение в компьютерном обучении имеют элементы игры, состязательности (например, подсчет очков и сравнение достижений различных учеников) или звуковые и зрительные эффекты (звучание музыкальных мелодий, мигание и цвета на экране дисплея).

Вот далеко неполный арсенал возможностей компьютера, делающих его очень перспективным для использования в учебном процессе обучающим средством.

(Приложение 3)   

 

 

 

 

 

 

 

 

 

IV. Ситуативный барьер.

 

Но никакое техническое средство не поможет, если ребёнок не хочет воспринимать изучаемый материал.

Ведь ситуативный барьер включает в себя и психологические особенности ребенка, например, особенности переходного возраста, когда подросток хочет быть как все и ему лень учить урок, если его друг гуляет. И не беда, что завтра контрольная работа или экзамен, сейчас у него не то настроение. Здесь, наряду с определением цели, необходима чёткая мотивация. Математика математикой, но все мы люди и иногда приходим в школу в плохом настроении. Понятно, что педагог обязан оставить все свои проблемы за порогом школы, но ребёнок этого сделать не может. Учитель говорит: «Ты должен запомнить это правило», а ученик в это время думает, что ЕГО должны понять и пожалеть. В этом заключается барьер внутреннего несогласия, преодолеть который можно только с помощью индивидуального или дифференцированного подхода.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V. Познавательная активность школьников.

 

    Познавательная деятельность – это единство чувственного восприятия, теоретического мышления и практической деятельности. Она осуществляется на каждом жизненном шагу, во всех видах деятельности и социальных взаимоотношений учащихся (производительный и общественно полезный труд, ценностно-ориентационная и художественно-эстетическая деятельность, общение), а также путем выполнения различных предметно-практических действий в учебном процессе (экспериментирование, конструирование, решение исследовательских задач и т.п.).  Но только в процессе обучения познание приобретает четкое оформление в особой, присущей только человеку учебно-познавательной деятельности или учении.

Обучение всегда происходит в общении и основывается на вербально-деятельностном подходе. Слово одновременно является средством выражения и познания сущности изучаемого явления, орудием коммуникации и организации практической познавательной деятельности учащихся.

Обучение, как и всякий другой процесс, связано с движением. Оно, как и целостный педагогический процесс, имеет задачную структуру, а следовательно, и движение в процессе обучения идет от решения одной учебной задачей к другой, продвигая учащегося по пути познания: от незнания к знанию, то неполного знания к более полному и точному. Обучение не сводится к механической «передаче» знаний, умений и навыков, т.к. обучение является двусторонним процессом, в котором тесно взаимодействуют педагоги и учащиеся: преподавание и учение.

Отношение учащихся к учению преподавателя обычно характеризуется активностью. Активность (учения, освоения, содержания и т.п.) определяет степень (интенсивность, прочность) «соприкосновения» обучаемого с предметом его деятельности.

В структуре активности выделяются следующие компоненты:

·      готовность выполнять учебные задания;

·      стремление к самостоятельной деятельности;

·      сознательность выполнения заданий;

·      систематичность обучения;

·      стремление повысить свой личный уровень и другие.

С активностью непосредственно сопрягается еще одна важная сторона мотивации учения учащихся это самостоятельность, которая связана с определением объекта, средств деятельности, её осуществления самим учащимся без помощи взрослых и учителей. Познавательная активность и самостоятельность неотделимы друг от друга: более активные школьники, как правило, и более самостоятельные; недостаточная собственная активность учащегося ставит его в зависимость от других и лишает самостоятельности.

Управление активностью учащихся традиционно называют активизацией. Активизацию можно определить как постоянно текущий процесс побуждения учащихся к энергичному, целенаправленному учению, преодоление пассивной и стерео типичной деятельности, спада и застоя в умственной работе. Главная цель активизации – формирование активности учащихся, повышение качества учебно-воспитательного процесса.

В педагогической практике используются различные пути активизации познавательной деятельности, основные среди них – разнообразие форм, методов, средств обучения, выбор таких их сочетаний, которые в возникших ситуациях стимулируют активность и  самостоятельность учащихся.

Наибольший активизирующий эффект на занятиях дают ситуации, в которых учащиеся сами должны:

ü    отстаивать свое мнение;

ü    принимать участие в дискуссиях и обсуждениях;

ü    ставить вопросы своим товарищам и преподавателям;

ü    рецензировать ответы товарищей;

ü    оценивать ответы и письменные работы товарищей;

ü    заниматься обучением отстающих;

ü    объяснять более слабым учащимся непонятные места;

ü    самостоятельно выбирать посильное задание;

ü    находить несколько вариантов возможного решения познавательной задачи (проблемы);

ü    создавать ситуации самопроверки, анализа личных познавательных и практических действий;

ü    решать познавательные задачи путем комплексного применения  известных им способов решения.

Можно утверждать, что новые технологии самостоятельного обучения имеют в виду, прежде всего повышение активности учащихся: истина добытая путем собственного напряжения усилий, имеет огромную познавательную ценность.

Отсюда можно сделать вывод, что успех обучения в конечном итоге определяется отношением учащихся к учению, их стремлению к познанию, осознанным и самостоятельным приобретение знаний, умений и навыков, их активностью.

 Никому не нравится навязывание чужих идей, поэтому лучше, если ребёнок сам придёт к какому-то выводу, а не получит его в готовом виде. Как говорят: «Услышал и забыл, увидел и запомнил, сделал и понял». Поэтому на уроках необходимо:

а)  создание   психологически  комфортных  условий  для умственного  труда; б) использование различных форм и методов работы, позволяющих вовлечь в работу каждого учащегося.  Кроме того, необходим контроль и самоконтроль.   К этому подвигают и новые педагогические технологии, которые необходимо изучать и брать на вооружение. Одной из таких технологий является технология развивающего обучения. Известно, что целью системы развивающего обучения является готовность к саморазвитию.

 

VI. Принципы развивающего обучения:

1. Принцип деятельности.

2. Принцип непрерывности.

3. Принцип целостного представления о мире.

4. Принцип минимакса.

5. Принцип психологической комфортности.

6. Принцип вариативности.

7. Принцип творчества.

Итак, моё представление об этих принципах, и примеры их применения на конкретных уроках.

1. Принцип деятельности.

В системе развивающего обучения каждый ученик сам приобретает знания в процессе своей мыслительной деятельности. К теме урока его должны подвести умелые вопросы учителя. Затем перед учеником встаёт проблема, и он сам ищет пути её решения: выдвигает различные гипотезы, проверяет их, делает выводы. Разрешив проблему, он приобретает новые знания.

Так, на уроке по теме «Отрезок. Сравнение отрезков» можно предложить детям соединить две точки линиями. У кого - то это будут кривые, у кого-то отрезок. Рассмотреть все возможные варианты. Сделать вывод, что между двумя соседними точками отрезок — самый краткий путь. Иначе слишком много точек необходимо обогнуть. Этот пример показывает, что в результате деятельности обучающиеся пришли к новому знанию об отрезке.

2.Принцип непрерывности.

Нить понятий, рассматриваемых на уроке, проходит через все этапы урока,  и выходит на домашнее задание и последующие уроки как знание необходимое для решения более сложных задач. Так, научившись решать квадратные уравнения, учащиеся 8-го класса легко справляются с проблемой решения биквадратных, а также более сложных уравнений, сводящихся к квадратным. Для этого можно предложить серию квадратных уравнений, например:

3х² + 10х + 3= 0; 3(2х + 1)² + 10(2х + 1) + 3; 3х⁴ + 10х + 3 = 0; 2(х²+ 3)² - 7(х²+ 3) + 3; 

3. Принцип целостного представления о мире.

На уроках ученик получает не только знания по математике, но и знания в области других наук, т.е. очень хорошо налажены межпредметные связи с физикой, химией с другими предметами, а иногда и с понятиями, выходящими за круг изучаемых в школе предметов: знания о мире, о природе. Так в 6 классе перед изучением темы «Модуль» можно решить такой кроссворд:

1. Знак отрицательного числа?

2.   Число,      задающее     положение     на числовом луче?

3.  Расстояние между точками?

4. Пройденное расстояние?

5.  Точка О на числовом луче?

6.  Выражение вида, ?  (Далее с новой строки)

Затем  обсудить,   что  такое модуль   и,  если  вариантов  объяснения  не найдётся,  рассказать о математическом смысле этого слова,  и предложить дома найти в толковом словаре другие его толкования. Если же кто-то знает,   что  это  такое  (например,   отсек космического  корабля),   то рассказать о другом, математическом смысле этого слова.

				М	И	Н	У	С
		К	О	О	Р	Д	И	Н	А	Т	А
				Д	Л	И	Н	А
			П	У	Т	Ь
Н	А	Ч	А	Л	О
Д	Р	О	Б	Ь

        

 

4. Принцип минимакса.

Каждый ребёнок должен уметь выполнять необходимый минимум (базисный уровень), и стремиться к максимуму (продвинутый уровень). Этого можно достичь с помощью дифференцированного подхода, но, не деля класс на «сильных» и «слабых», а лишь предложив, например, разноуровневую самостоятельную работу, где каждый сам определит свой уровень.

ПРИМЕР:

Изучив в 5 классе тему «Сложение и вычитание смешанных чисел», можно дать такую работу: «Реши примеры и составь слова»

1). 5 +  , 2). , 3). , 4). , 5). , 6). 8 - , 7). 5 - , 8). , 9). , 10). , 11)..

Среди букв, из которых ученик будет составлять слова, есть такие, которые соответствуют неправильным ответам, причём, это самые распространённые ошибки. Ответы: ф - ; м - ; у - ; о - ; ы - ; л - ; ь - ; д - ; б - ; п - ; е - ; с - ; ц - ; т - ; я - .

Тот ученик, который выполнит пять примеров, получит слово

«МОЛОД» можно сказать, что он ещё не заслужил оценку или только три; тот, кто решит 7 примеров, будет «МОЛОДЕЦ» (оценка 4);

ну, а если решены все 11 примеров - «МОЛОДЕЦ, ПЯТЬ». 

Такая дифференцированная работа не унизит ученика и заставит на следующем уроке стараться больше. Этот пример можно отнести и к

5. Принцип психологической комфортности.

Добавить здесь можно лишь то, что все гипотезы, выдвигаемые учениками, принимаются и проверяются. Тогда каждый ребёнок чувствует свою причастность к происходящему на уроке.

6 Принцип вариативности.

Решение одной задачи несколькими способами порой продуктивнее, чем решение множества не связанных между собой задач.  

Так, например,   задача 5-го класса

«Молочный бидон, наполненный молоком, весит 35 кг. Наполовину заполненный

тот же бидон весит 18,5 кг. Сколько весит пустой молочный бидон?», решается

несколькими способами, которые помогут ребёнку разобраться в величинах и

выбрать для себя самый понятный способ решения.

Способы решений:

I 1) 35- 18,5 = 16,5(кг) - весит половина имеющегося молока.

2) 16,5 х 2 = 33 (кг) - весит всё молоко,

3) 35 - 33 = 2(кг) - весит пустой бидон.

Ответ: 2 кг.

II. 1) 18_:5 х2 = 37(кг) - весит всё молоко и два пустых бидона. 2) 37- 35 = 2(кг) - весит пустой бидон.

Ответ: 2 кг.

III. 1)35 х 2 = 70(кг) - весит два бидона с молоком.

2) 18,5x2 = 37(кг) - весит молоко и два пустых бидона.

3) 70- 37 = ЗЗ (кг) - весит всё молоко,

4) 35- 33 - 2 (кг) - весит пустой бидон.

Ответ: 2 кг.

IV. Пусть х кг. весит бидон, тогда молоко без бидона весит (35 -х) кг. или (18,5 - х) х2. Получим   уравнение: 35-х -(18,5 - х) х2_, решая которое, получим нужный ответ. Или 53 + х = 18,5x2.

И т.д. Просмотрев все способы решения можно обратить внимания на более рациональные, но нельзя отвергать, ни один из способов. Кроме того, можно задать задание: «Решить задачу различными способами» и хорошую оценку поставить тому, кто решит её самым большим количеством способов.

7. Принцип творчества.

На протяжении всего урока ребёнок занимается творческой учебной деятельностью, которая является аналогом научного творчества. В качестве домашнего задания можно предложить классу составить кроссворд, ребус, шифровку, решить задачи или уравнения максимально возможным количеством способов, нарисовать картинку к задаче и т.п. тогда каждый найдёт для себя посильное задание.

(Приложение 4)   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

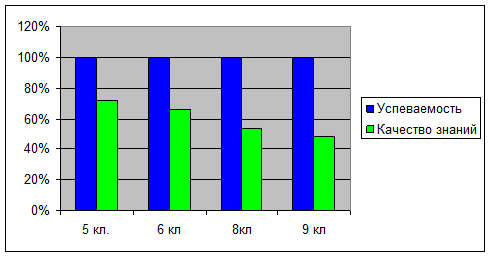
Результативность

Веду систематический мониторинг результативности обучения. Процент качества обучения составляет по итогам 2010г

 

Математика  5 кл.

                                                                                    Алгебра 7 кл

 

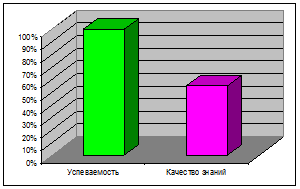
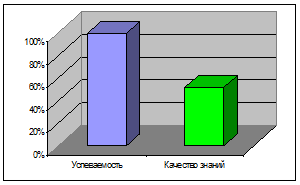
Алгебра 8 кл.                                                                   Алгебра 9 кл.

 

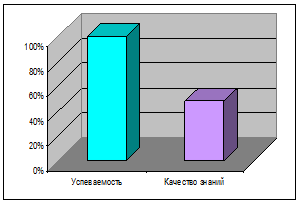
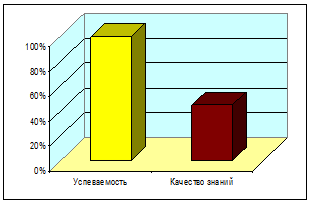
I полугодие 2011 года.

 

 

Заключение

 

Современный этап развития российского образования характеризуется широким внедрением в учебный процесс новых технологий в том числе и компьютерных. Они позволяют выйти на новый уровень обучения, открывают ранее недоступные возможности как для учителя, так и для учащегося. Информационные технологии находят свое применение в различных предметных областях на всех возрастных уровнях, помогая лучшему усвоению как отдельных тем, так и изучаемых дисциплин в целом. Персональный компьютер (ПК) помогает учащимся самоутверждаться, реализовывать свои знания в практической деятельности, творчески решать учебные задания, позволяет активизировать обучающихся во время урока. Сегодня целесообразность применения новых технологий в среднем и старшем звеньях школьной системы очевидна. Навыки пользователя ПК и рынок обучающих программ, мультимедийных справочников, Интернет открывают большие возможности самообразования. Использование на уроках мультимедийного проектора поднимают процесс обучения на качественно новый уровень. Нельзя сбрасывать со счетов и психологический фактор: современному ребенку намного интереснее воспринимать информацию именно в такой форме, нежели при помощи устаревших схем и таблиц. При использовании мультимедийного проектора на уроках информация представляется не статичной неозвученной картинкой, а динамичными видео- и звукорядом, что значительно повышает познавательный интерес школьников и эффективность усвоения материала  интерактивные же элементы обучающих программ позволяют перейти от пассивного усвоения к активному, так как учащиеся получают возможность самостоятельно моделировать явления и процессы, воспринимать информацию не линейно, с возвратом, при необходимости, к какому-либо фрагменту, с повторением виртуального эксперимента с теми же или другими начальными параметрами.

Хорошо понимая причины, препятствующие восприятию математики, приходишь к выводу, что повышение творческой активности на уроках способствуют повышению качества знаний учащихся. Уроки с применением мультимедийного проектора вызывают у учащихся интерес, заставляют работать всех. Использование мультимедиа на практических занятиях превращает их в творческий процесс, позволяет осуществить принципы развивающего обучения, позволяет формировать и развивать познавательную мотивацию школьников к получению новых знаний, помогает создавать условия успешности каждого ученика на уроке, значительно улучшает четкость в организации работы класса или группы учащихся. Качество знаний при этом заметно возрастает.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список литературы:

 

¨ Гуреева М.Г.  Лекция по информатике на курсах в ИУУ 2003г.

¨ Применение новых информационных технологий в образовательном процессе/ С.П. Новиков//Педагогика. –2003. - №9. с. 25 – 28.      Берлинер, Е.М. Microsoft Windows XP/ Е.М. Берлинер, И.Б. Глазырина, Б.Э.Глазырин.-М., 2004. – 509 с.

¨ Шейнина О.С, Соловьева Г.М, Математика. Занятия математического кружка, 5 – 6 классы, М., Издательство НЦ ЭНАНС,2003 г.

¨ Захарова, И. Г. Информационные технологии в образовании: учебное пособие для студ. пед. учеб. заведений/ И. Г. Захарова,– М.: Издательский центр «Академия», 2003. – 192 с.

¨ «Конструирование современного урока математики», С.Г.Манвелов, М., Просвещение, 2002 г.

¨ Лыскова, В. Ю. Активизация учебно-познавательной деятельности учащихся на уроках информатики в условиях учебно-информационной среды/ В. Ю. Лыскова, - Тамбов, Издательство Стиль - 1997. – 380 с. 

¨ Методические разработки Савченко Е.М. МОУ гимназия №1 г. Полярные Зори, Мурманской обл.