На прошлом уроке мы научились находить площадь прямоугольника и квадрата. Как найти площадь прямоугольника? По какой формуле вычисляется площадь квадрата?

    На прошлом уроке мы с вами вычисляли площади многоугольников, составленных из квадратов. Сегодня мы продолжим изучать способы вычисления площади многоугольников на клетчатой бумаге.

   Выполните самостоятельно два задания на раздаточных листах.  

2.      Вычислите площадь многоугольника

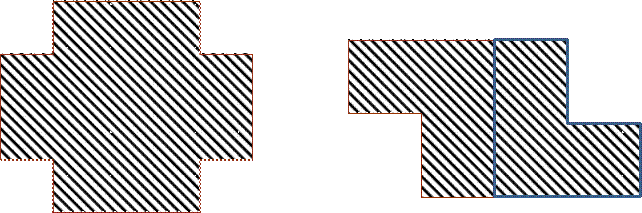
«Решение задач – практическое искусство, подобно плаванию, катанию на лыжах или игре на фортепиано, научиться ему можно, только подражая хорошим образцам и постоянной тренировкой» 

Д. Пойа

     На уроках математики всегда используют тетради в клетку. Почему?

     Но вы вряд ли  представляете, насколько мощным инструментом является клетка для геометрических построений и для решения задач на клетчатой бумаге.

     «Клетка – ты чудо!  Загадочна, проста и таинственна.  Сколько возможностей, открытий хранишь в себе.  Сколько закономерностей можно раскрыть, благодаря этому «Чуду»!»      Сегодня мы с вами будем решать задачи на клетчатой бумаге. Задачи на нахождение площади многоугольников.

Использование способа подсчета клеток

Задача 1. Найти площадь многоугольника,  если площадь одной клетки 1см² 

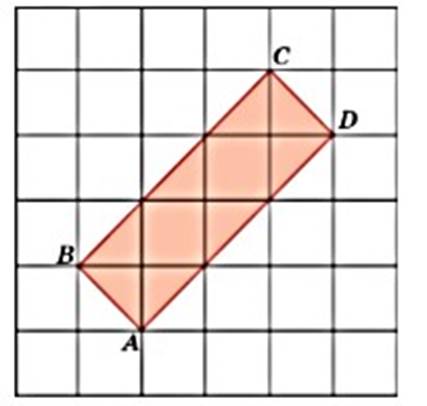Решение: Многоугольник состоит из 2 целых клеток и 8 половинок, значит его площадь будет равна 2 + 4 =

6     (см²)

Достраивание до квадрата или прямоугольника

Задача 2.  Найти площадь фигуры АВСД. Размер клетки 1 см²

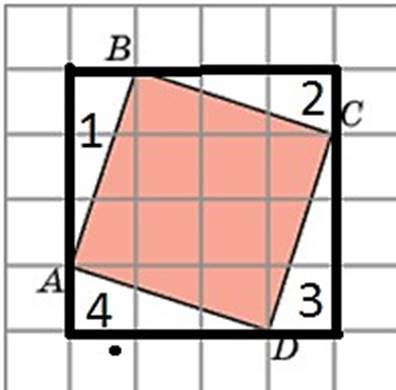Решение: Достроим около фигуры квадрат со стороной 4 клетки. Для того, чтобы найти площадь розовой фигуры надо из площади квадрата вычесть площадь 4 одинаковых треугольников. 

Значит S = 4·4 - 4·3·1: 2 = 10 (см²)

Разбиение фигуры на части

Задача 2. Найти площадь многоугольника, если площадь одной клетки равна 1 см² 

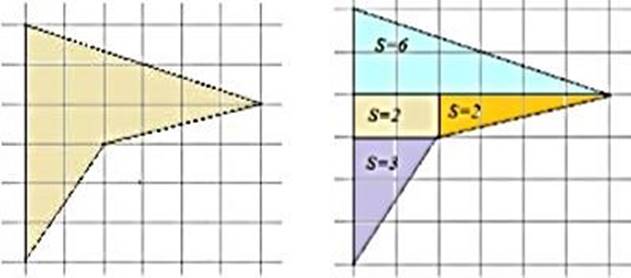
Решение: Разобьем фигуру на прямоугольные треугольники и прямоугольники или квадраты. Площадь голубого

треугольника равна 2ˑ6 :2=6см², площадь рыжего - 1·4:2=2см², площадь сиреневого - 2·3:2=3см², площадь прямоугольника равна 1·2 =2см². Значит площадь всей фигуры будет равна сумме всех частей S = 6см²+2см²+3см²+ 2см² = 13см²

Вывод: Способы достраивания и способ разбиения подходят  для нахождения площадей любых многоугольников, с вершинами в узлах решетки, но они очень трудоемкие.

        Нет ли способа полегче?

Нахождение площади многоугольника  по формуле Пика

   Формула была открыта в 1899году австрийским математиком Георгом Пиком. Формула применяется для вычисления площади многоугольника, вершины которого располагаются в узлах квадратной сетки.

   Она связывает площадь многоугольника с количеством

узлов, лежащих внутри и на границе многоугольника,

S = Г : 2 + В – 1,

где  S – площадь многоугольника;

       Г – количество узлов сетки, попадающих на стороны многоугольника (на границе многоугольника)

       В – количество узлов сетки, расположенных внутри многоугольника (внутренние точки многоугольника)

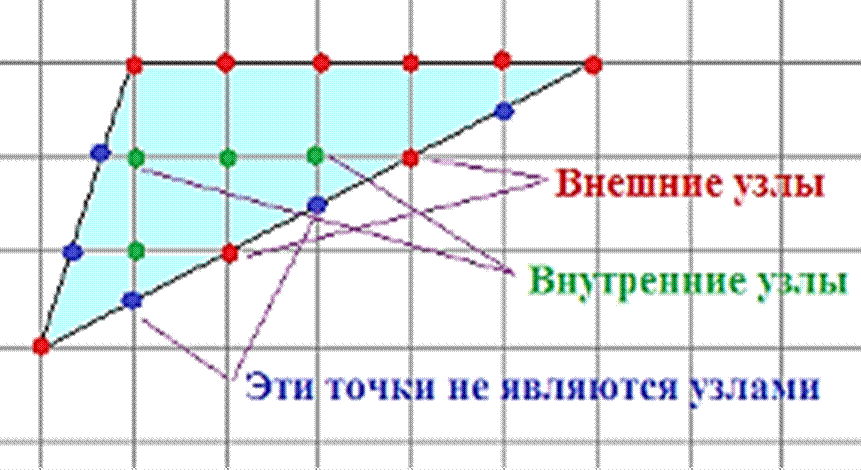
S = Г : 2 + В – 1

Георг Алекса́ндр Пик  ( 10 августа 1859 — 13 июля 1942) — австрийский математик, родился в еврейской семье.

Круг математических интересов  Пика был чрезвычайно широк. Им написаны  работы в области математического  анализа, дифференциальной  геометрии, в теории дифференциальных уравнений  и т. д., всего  более  50 тем. 

Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники.

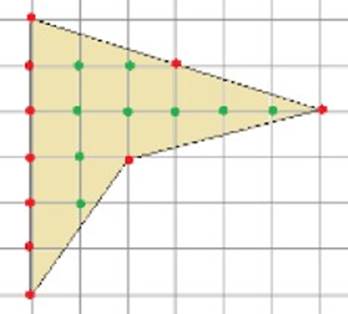Вернемся  к нашей задаче №3.    Решим её по формуле Пика.  Для этого расставим точки в  углах решетки: красные - на  границе фигуры, зеленые –  внутри фигуры и посчитаем их

Г = 10  В = 9

S = Г: 2 + В − 1

S = 10:2 + 9 – 1 = 13(см²) 

Вывод: Этот способ универсальный и наименее  трудоемок, но если клетки мелкие и рисунок не четкий, можно ошибиться в подсчете точек в узлах решетки.

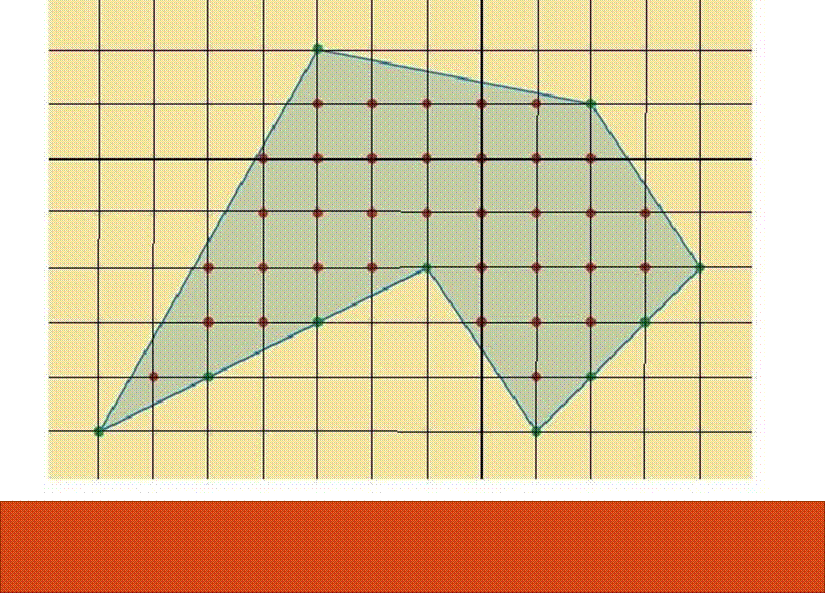
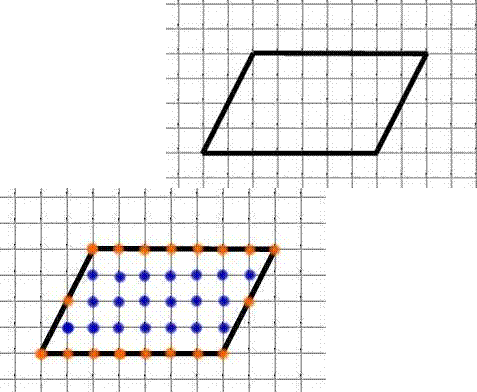Найдём площадь параллелограмма по формуле Пика:

Отметим узлы:

Г = 18 (обозначены красным) В = 20 (обозначены синим)

                    S = 18:2 + 20 – 1 = 28 (см²) Найдём площадь произвольного треугольника  по формуле Пика:

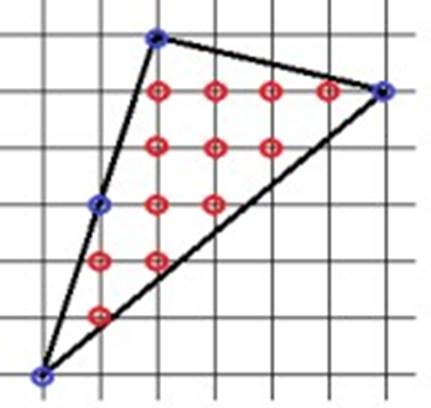
Г = 4,   В = 12

S = 4: 2 + 12 – 1 = 13 ( см²)

      По формуле Пика нельзя вычислить площадь правильного треугольника, пятиугольника, шестиугольника и т.д. Длины их сторон нельзя расположить у узлах квадратной решетки. 

      Использование   формулы     Пика   для нахождения площади кругового сектора или кольца нецелесообразно, так как она даёт приближённый результат.

Физкультминутка

Дружно с вами мы решали,  Много, много  рассуждали,  А теперь все дружно встали,  Свои косточки размяли. 

На счет раз кулак сожмем,  На счет два в локтях согнем.  На счет три - прижмем к плечам,  На четыре – к небесам. На счет 5 – сильней прогнулись,  И друг другу улыбнулись.  На счет 6 – садимся снова   И продолжить все готовы.

А теперь решаем самостоятельно

Г = 14;       В = 4;        S = 14:2 + 4 – 1 = 10

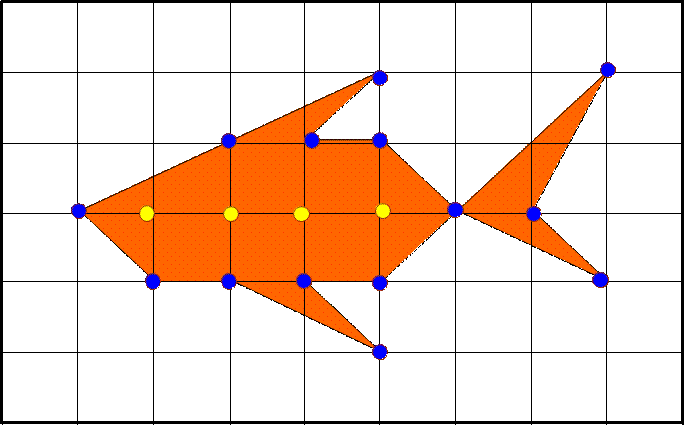
Вычислим площадь многоугольника по формуле Пика

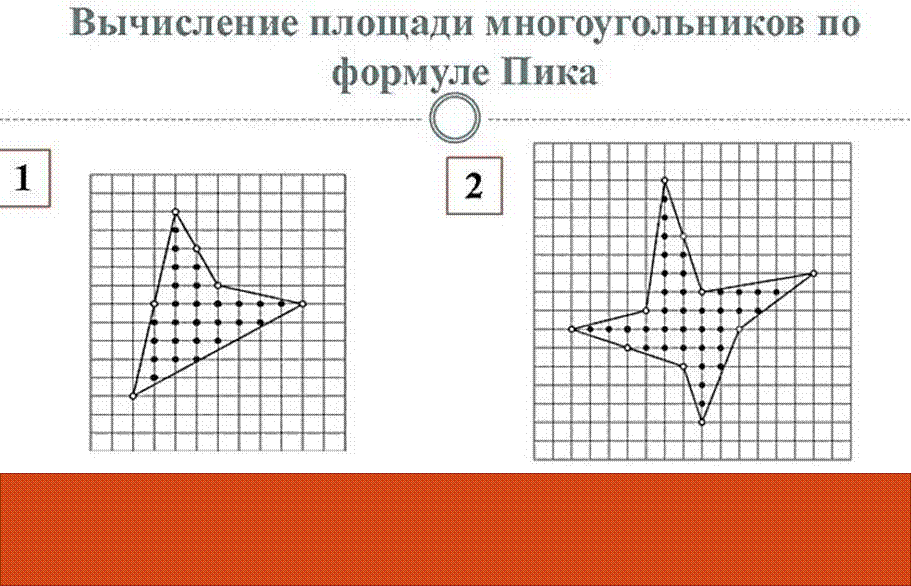
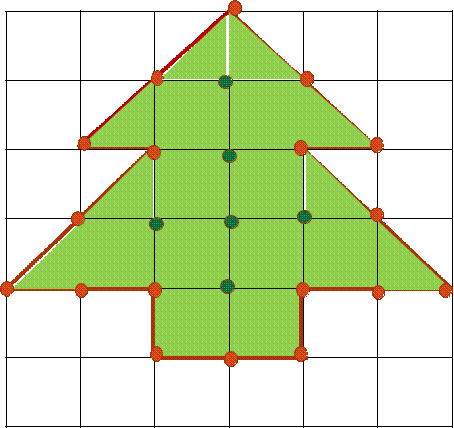
S = 14

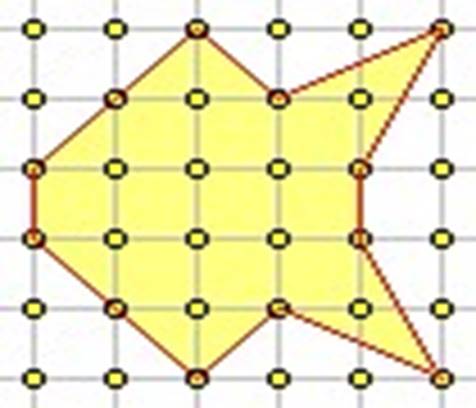
S = 15

Выполните задание по  QR - кодам

№№ 589, 590

Использованные  ресурсы

https://images.app.goo.gl/CdFZAkRwLLm5N3MJ7 https://images.app.goo.gl/b3FDrzAprDYqCf347 https://images.app.goo.gl/4hCw7ukpcy3irKDk9 https://images.app.goo.gl/GkmkwSpghDWhGUHN6 https://images.app.goo.gl/xHqh1SAehfZDYU3U9 https://images.app.goo.gl/gzfvB7rhX2t8s6u99 https://images.app.goo.gl/SVL51PDXjf8oQ63dA https://images.app.goo.gl/8h5J14fAwbEHk5Z9A https://images.app.goo.gl/kHNmzc5pZcuWPwK98 https://images.app.goo.gl/kcHsPQQYAm1UEeQ77 https://images.app.goo.gl/5TbPMTwrVgArczpX7 https://images.app.goo.gl/w1rfZe2pbK3fz5P26 https://images.app.goo.gl/TNPFbt2iw3ZYuTyq8 https://images.app.goo.gl/LHUXQrrVwoS9UdZU8 https://yandex.kz/collections/card/59fa06a7be1d77124b4166cc/