


Сегодня на занятии
• Выясним геометрический смысл производной функции.
• Выведем уравнение касательной к графику дифференцируемой функции.









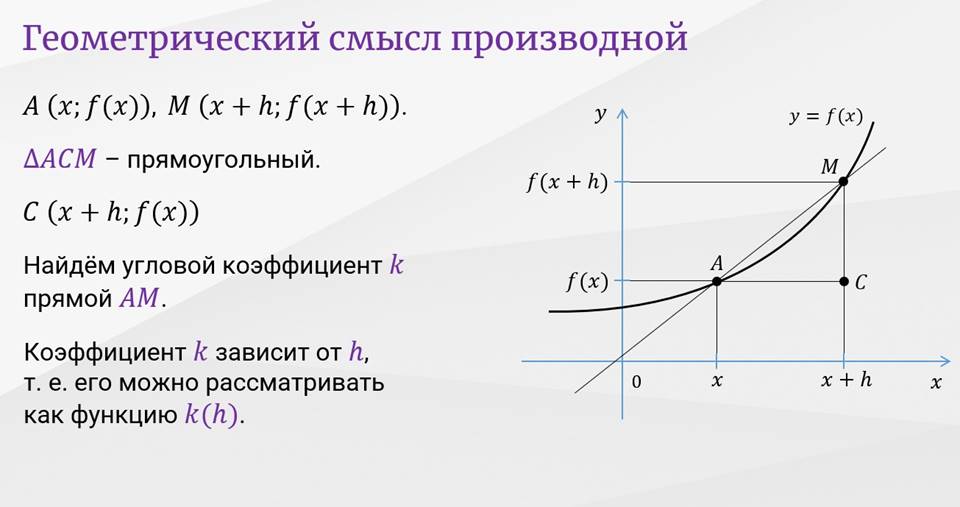

 |
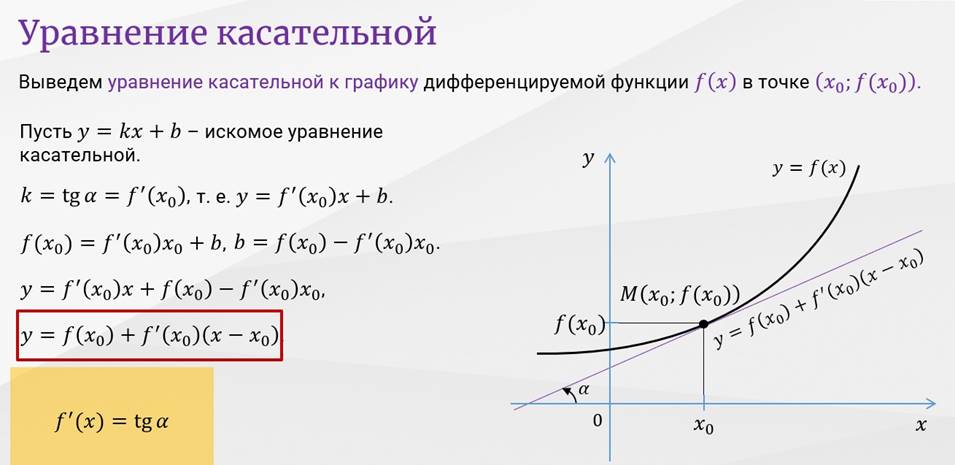
Геометрический смысл производной
![]() Пример:
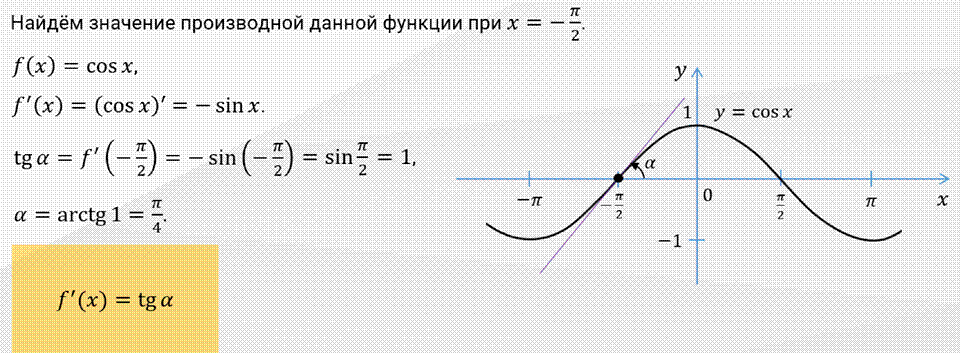
Найти угол между касательной к графику функции 𝑦 = 𝑐𝑜𝑠𝑥
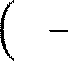
в точке −
𝜋 ; 0 и осью Ох 2 Решение:
Пример:
Найти угол между касательной к графику функции 𝑦 = 𝑐𝑜𝑠𝑥
в точке −
𝜋 ; 0 и осью Ох 2 Решение:
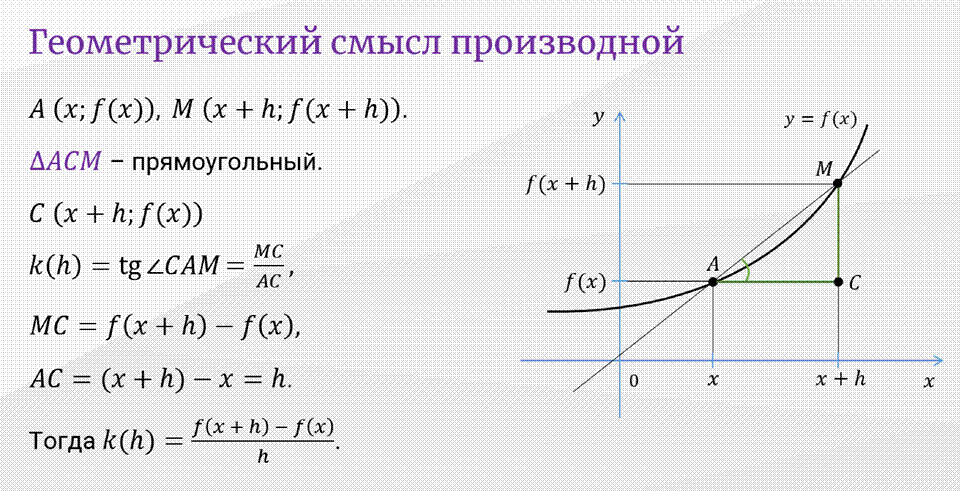
Геометрический смысл производной
![]() Пример:
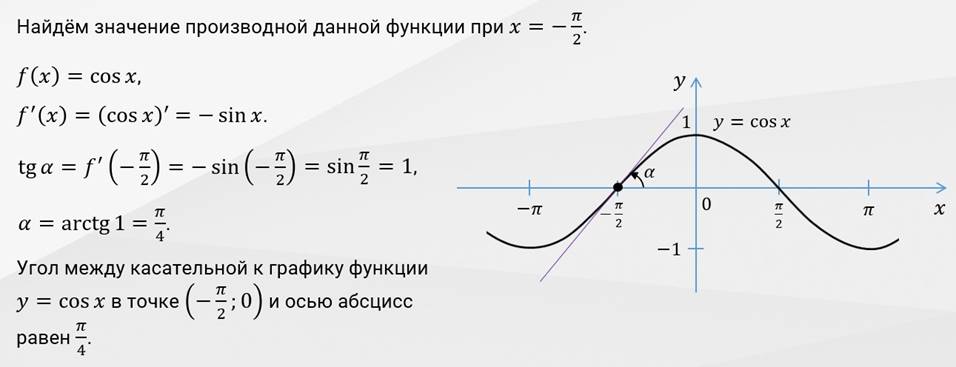
Найти угол между касательной к графику функции 𝑦 = 𝑐𝑜𝑠𝑥
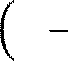
в точке −
𝜋 ; 0 и осью Ох 2 Решение:
Пример:
Найти угол между касательной к графику функции 𝑦 = 𝑐𝑜𝑠𝑥
в точке −
𝜋 ; 0 и осью Ох 2 Решение:
 |
Пример: Найти
уравнение касательной к графику функции 𝑦 = 3𝑠𝑖𝑛𝑥
в точке с абсциссой 𝑥0 = ![]() 𝜋3 Решение:
𝜋3 Решение:
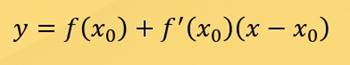
Пример: Найти
уравнение касательной к графику функции 𝑦 = 3𝑠𝑖𝑛𝑥
в точке с абсциссой 𝑥0 = ![]() 𝜋3
𝜋3

Пример:
Найти уравнение касательной к графику функции 𝑦 = 3𝑠𝑖𝑛𝑥
в точке с абсциссой 𝑥0 = ![]() 𝜋3
𝜋3
Найдите угловой коэффициент касательной к графику функции 𝑦 = 𝑓(𝑥) в точке с абсциссой 𝑥0:
![]()
![]() 𝜋2 + 2𝑥, 𝑥0 = 1.
𝜋2 + 2𝑥, 𝑥0 = 1.
![]() а) 𝑓 𝑥 =
2 cos 𝑥, 𝑥0
= 2; б)
𝑓
𝑥 = 𝑥
а) 𝑓 𝑥 =
2 cos 𝑥, 𝑥0
= 2; б)
𝑓
𝑥 = 𝑥
Найдите угловой коэффициент касательной к графику функции 𝑦 = 𝑓(𝑥) в точке с абсциссой 𝑥0:
![]()
![]() 𝜋2 + 2𝑥, 𝑥0 = 1.
𝜋2 + 2𝑥, 𝑥0 = 1.
![]() а) 𝑓 𝑥 = 2 cos 𝑥, 𝑥0 = 2; б) 𝑓 𝑥 =
𝑥 Решение:
а) 𝑓 𝑥 = 2 cos 𝑥, 𝑥0 = 2; б) 𝑓 𝑥 =
𝑥 Решение:
 а) 𝑓
𝑥 = 2 cos 𝑥, 𝑥0 =
а) 𝑓
𝑥 = 2 cos 𝑥, 𝑥0 = ![]() 𝜋2;
𝑓′(𝑥)
= 2 cos 𝑥
𝜋2;
𝑓′(𝑥)
= 2 cos 𝑥![]() ′ =
−2 sin 𝑥
′ =
−2 sin 𝑥
𝑘 = 𝑓′ 𝑥0 =
−2 sin ![]() 𝜋2 =
−2.
𝜋2 =
−2.
Ответ: а) −2;
Найдите угловой коэффициент касательной к графику функции 𝑦 = 𝑓(𝑥) в точке с абсциссой 𝑥0:
![]()
![]() 𝜋2 + 2𝑥, 𝑥0 = 1.
𝜋2 + 2𝑥, 𝑥0 = 1.
![]() а) 𝑓 𝑥 =
2 cos 𝑥, 𝑥0
= 2; б)
𝑓
𝑥 = 𝑥
а) 𝑓 𝑥 =
2 cos 𝑥, 𝑥0
= 2; б)
𝑓
𝑥 = 𝑥
Решение:
![]()
 б)
𝑓
𝑥 = 𝑥2 + 2𝑥, 𝑥0
= 1; 𝑓′(𝑥) = 𝑥2
+ 2𝑥
б)
𝑓
𝑥 = 𝑥2 + 2𝑥, 𝑥0
= 1; 𝑓′(𝑥) = 𝑥2
+ 2𝑥![]() ′ = 2𝑥
+ 2 𝑘 = 𝑓′ 𝑥0 = 2 ∙ 1
+ 2
=
4.
′ = 2𝑥
+ 2 𝑘 = 𝑓′ 𝑥0 = 2 ∙ 1
+ 2
=
4.
Ответ: б) 4.
Найдите угол между касательной к графику функции 𝑦 = 𝑓(𝑥) в точке с абсциссой 𝑥0 и осью 𝑂𝑥:
![]() 1 3 − 𝑥,
𝑥0
= 2.
1 3 − 𝑥,
𝑥0
= 2.
![]()
![]() а) 𝑓
𝑥 = ln𝑥, 𝑥0 = 1;
б) 𝑓
𝑥 = 3𝑥
а) 𝑓
𝑥 = ln𝑥, 𝑥0 = 1;
б) 𝑓
𝑥 = 3𝑥
Найдите угол между касательной к графику функции 𝑦 =𝑓(𝑥) в точке с абсциссой 𝑥0 и осью 𝑂𝑥:
![]() 1 3 − 𝑥,
𝑥0
= 2.
1 3 − 𝑥,
𝑥0
= 2.
![]()
![]() а) 𝑓
𝑥 = ln𝑥, 𝑥0 = 1;
б) 𝑓
𝑥 = 3𝑥
а) 𝑓
𝑥 = ln𝑥, 𝑥0 = 1;
б) 𝑓
𝑥 = 3𝑥
Решение:
![]() а) 𝑓 𝑥 =
ln 𝑥, 𝑥0
= 1;
а) 𝑓 𝑥 =
ln 𝑥, 𝑥0
= 1;
1
𝑓′(𝑥) =
![]() ln 𝑥
ln 𝑥![]() ′
=
′
=
![]()
𝑥
![]() tg 𝛼
= 𝑓′ 𝑥0 =
tg 𝛼
= 𝑓′ 𝑥0 = ![]() = 1
= 1
𝜋
𝛼 = arctg 1 = ![]() .
.
4
𝜋
Ответ: а) ![]() ;
;
4
Найдите угол между касательной к графику функции 𝑦 = 𝑓(𝑥) в точке с абсциссой 𝑥0 и осью 𝑂𝑥:
![]() 1 3 − 𝑥,
𝑥0
= 2.
1 3 − 𝑥,
𝑥0
= 2.
![]()
![]() а) 𝑓
𝑥 = ln𝑥, 𝑥0 = 1;
б) 𝑓
𝑥 = 3𝑥
а) 𝑓
𝑥 = ln𝑥, 𝑥0 = 1;
б) 𝑓
𝑥 = 3𝑥
Решение:
![]()
![]() б) 𝑓 𝑥 =𝑥
б) 𝑓 𝑥 =𝑥
13 3 − 𝑥, 𝑥0 = 2;

![]() 𝑓′(𝑥)
= 1 𝑥3 − 𝑥′ =
𝑥2 − 1,
𝑓′(𝑥)
= 1 𝑥3 − 𝑥′ =
𝑥2 − 1,
3
tg 𝛼 = 𝑓′ 𝑥0 = 22 − 1 = 3, 𝛼 = arctg 3.
Ответ: б) arctg 3.
Напишите уравнение касательной к графику функции 𝑦 = 𝑓(𝑥) в точке с абсциссой 𝑥0:
![]()
![]() а) 𝑓
𝑥 = 𝑥3 − 1, 𝑥0
= −1; б) 𝑓 𝑥 = 𝑥
+
а) 𝑓
𝑥 = 𝑥3 − 1, 𝑥0
= −1; б) 𝑓 𝑥 = 𝑥
+
![]() 𝑥 +1 1,
𝑥0
= 0.
𝑥 +1 1,
𝑥0
= 0.
Напишите уравнение касательной к графику функции 𝑦 = 𝑓(𝑥) в точке с абсциссой 𝑥0:
![]()
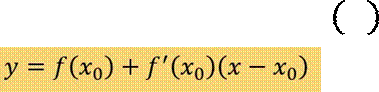 а) 𝑓
𝑥 = 𝑥3 − 1, 𝑥0
= −1; б) 𝑓 𝑥 = 𝑥
+
а) 𝑓
𝑥 = 𝑥3 − 1, 𝑥0
= −1; б) 𝑓 𝑥 = 𝑥
+
![]() 𝑥 +1 1,
𝑥0
= 0.
𝑥 +1 1,
𝑥0
= 0.
Решение:
 а) 𝑓 𝑥 = 𝑥3 −
1, 𝑥0
= −1; 𝑓
𝑥0 = (−1)3−1 = −2,
а) 𝑓 𝑥 = 𝑥3 −
1, 𝑥0
= −1; 𝑓
𝑥0 = (−1)3−1 = −2,
𝑓′(𝑥) =
![]() 𝑥3 − 1
𝑥3 − 1![]() ′
=
3𝑥2,
′
=
3𝑥2,
𝑓′(𝑥0) = 3(−1)2= 3,
𝑦 = −2 + 3![]() 𝑥
+ 1
𝑥
+ 1![]()
𝑦 = −2 + 3𝑥 + 3, 𝑦 = 3𝑥 + 1
Ответ: а) 𝑦 = 3𝑥 + 1,
Напишите уравнение касательной к графику функции 𝑦 = 𝑓(𝑥) в точке с абсциссой 𝑥0:
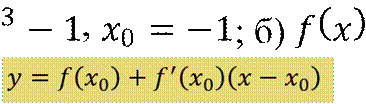 1
1
![]() а)
𝑓
𝑥 = 𝑥 = 𝑥 +
а)
𝑓
𝑥 = 𝑥 = 𝑥 +
![]() 𝑥 + 1,
𝑥0
= 0.
𝑥 + 1,
𝑥0
= 0.
Решение:
1
 б) 𝑓 𝑥 =
𝑥 +
б) 𝑓 𝑥 =
𝑥 + ![]() 𝑥 + 1, 𝑥0 = 0;
𝑥 + 1, 𝑥0 = 0;
𝑓
𝑥0 = 0 + 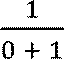 = 1,
= 1,
![]() 𝑓′(𝑥)
=
𝑓′(𝑥)
= ![]() 𝑥 + 𝑥
+1
1
′ = 1 − 𝑥
+11 2 ,
𝑥 + 𝑥
+1
1
′ = 1 − 𝑥
+11 2 ,
![]() 𝑓′
𝑥0 = 1 −
𝑓′
𝑥0 = 1 − 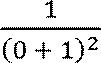 =0
=0
𝑦 = 1 + 0![]() 𝑥
− 0
𝑥
− 0![]() ,
𝑦 = 1. Ответ:
б)
𝑦
= 1.
,
𝑦 = 1. Ответ:
б)
𝑦
= 1.

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.