Сегодня на занятии

•       Вспомним,  что  называют наибольшим и наименьшим значениями функции.

•       Научимся находить наибольшее и наименьшее значения функции на отрезке.

Говоря о наибольшем или наименьшем значении функции, её рассматривают на всей области определения или на числовом промежутке

(отрезке, интервале и так далее), который является подмножеством области определения.

Пусть функция 𝑦 = 𝑓 𝑥 определена на числовом множестве 𝑋.

Число 𝑀 называется наибольшим значением функции 𝑦 = 𝑓 𝑥

на числовом множестве 𝑋, если существует 𝑥₀ из 𝑋 такое, что 𝑓𝑥₀ = 𝑀, и для любого 𝑥 из 𝑋 выполняется неравенство 𝑓 𝑥 ≤ 𝑀.

Пусть функция 𝑦 = 𝑓 𝑥 определена на числовом множестве 𝑋.

Число 𝑚 называется наименьшим значением функции 𝑦 = 𝑓 𝑥

на числовом множестве 𝑋, если существует 𝑥₀ из 𝑋 такое, что 𝑓𝑥₀ = 𝑚, и для любого 𝑥 из 𝑋 выполняется неравенство 𝑓 𝑥 ≥ 𝑚.

2. Наибольшего и наименьшего значений

непрерывная функция может достигать как на концах отрезка, так и внутри него.

3.Если наибольшее (наименьшее значение) достигается внутри отрезка, то только в стационарной или критической точке.

Наибольшие и наименьшие значения функции

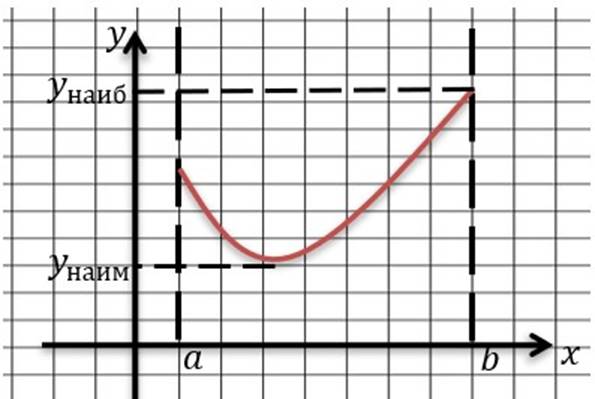
Пусть функция 𝑓(𝑥) непрерывна на отрезке 𝑎; 𝑏 и имеет несколько критических точек на этом отрезке.

Для нахождения наибольшего и наименьшего значений функции на отрезке 𝑎;𝑏 нужно:

1)     найти значения функции на концах отрезка, т. е.

числа 𝑓(𝑎) и 𝑓(𝑏);

2)     найти её значения в тех критических точках, которые принадлежат интервалу (𝑎; 𝑏);

3)     из всех найденных значений найти наименьшее

(это будет 𝑦_наим) и наибольшее (это будет 𝑦_{наибmirea.ru}).

Найдите её наибольшее и наименьшее значения.

Найдите её наибольшее и наименьшее значения.

Решение:

𝑓 −1     = (−1)³−6 ∙ −1² + 9 = 2,

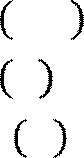𝑓 2     = 2³ − 6 ∙ 2² + 9 = -7

𝑓^′ 𝑥        = 𝑥³ − 6𝑥² + 9^′ = 3𝑥² − 12𝑥,

3𝑥² − 12𝑥 = 0,

3𝑥𝑥 − 4 = 0,

𝑥₁ = 0, 𝑥₂ = 4.

𝑥₁ ∈ (−1; 2), 𝑥₂ ∉ (−1; 2).

Найдите её наибольшее и наименьшее значения.

Решение:

𝑓 0 = 0³ − 6 ∙ 0² + 9 = 9.

Наибольшее значение функции на отрезке [−1; 2ሿ равно 9, а наименьшее значение равно −7.

 𝑓наиб.(𝑥) = 9, 𝑓наим.(𝑥) = −7.

𝑥 ∈ [−1; 2ሿ      𝑥 ∈ [−1; 2ሿ

Наибольшие и наименьшие значения функции

Наибольшее и наименьшее значения функции часто приходится находить не на отрезке, а на интервале.

Встречаются задачи, в которых функция 𝑓(𝑥) имеет на заданном интервале одну стационарную точку – точку минимума или точку максимума.

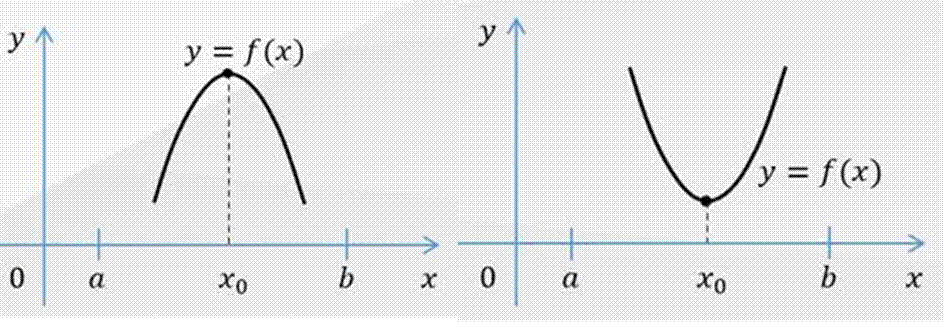
Наибольшие и наименьшие значения функции

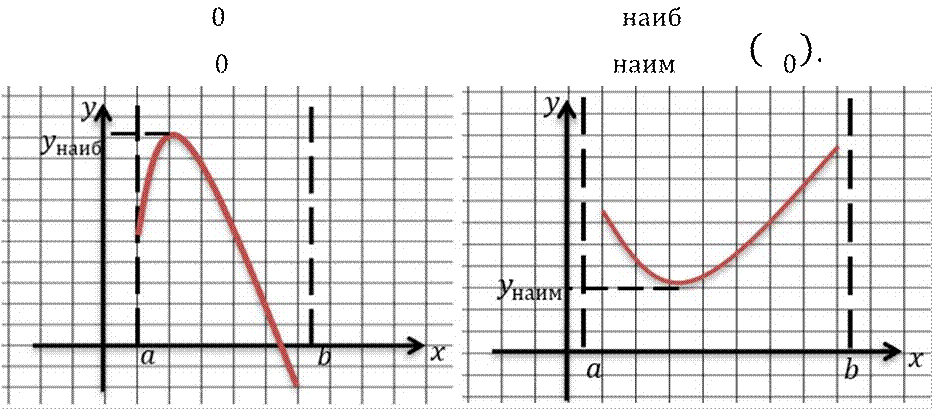Теорема. Пусть функция 𝑦 = 𝑓(𝑥) непрерывна на промежутке 𝑋 и имеет внутри него единственную стационарную или критическую точку 𝑥 = 𝑥₀. Тогда: а) если 𝑥 = 𝑥 − точка максимума, то 𝑦 = 𝑓(𝑥₀);

б) если 𝑥 = 𝑥 − точка минимума, то 𝑦    = 𝑓 𝑥

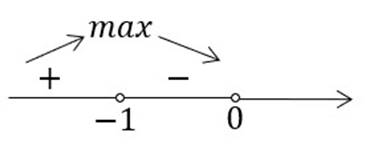
Пример: Найти наибольшее и

𝟏 наименьшее значения функции 𝒚 = 𝒙 +

𝒙

на промежутке (−∞; 𝟎).

Решение:

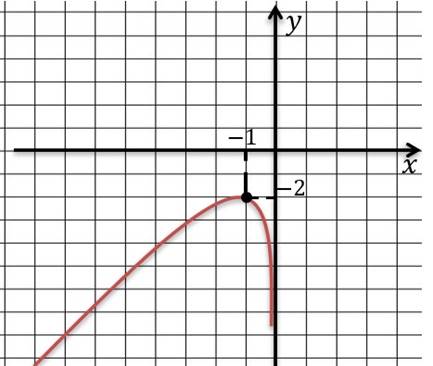
′ 𝑥        = 1 − 𝑥12

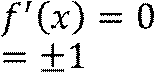 ⇔ 𝑥² = 1 ⇔ 𝑥

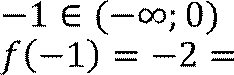 𝑦наиб

Пример:  Найти наибольшее и наименьшее значения функции

Решение:

𝑓^′ 𝑥        = 3𝑥² − 4𝑥

функций:

а) 𝑓 𝑥 = (𝑥 + 2)²(𝑥 − 3)³, −3;1;

функций:

Решение: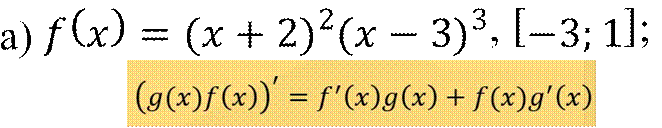

𝑓 −3      = (−3 + 2)²(−3 − 3)³ = −216,

𝑓 1 = (1 + 2)²(1 − 3)³= −72.

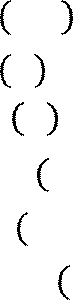𝑓^′ 𝑥      =        𝑥 + 2 ² 𝑥 − 3^′ =

= 2 𝑥 + 2        𝑥 − 3 ³ + 3(𝑥 + 2)²(𝑥 − 3)²=

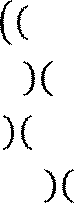
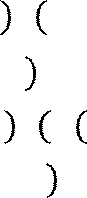= 𝑥 + 2          𝑥 − 3 ² 2 𝑥 − 3 + 3(𝑥 + 2) =

= 5𝑥 𝑥 + 2       𝑥 − 3 ²,

функций:

а) 𝑓 𝑥 = (𝑥 + 2)²(𝑥 − 3)³, −3;1;

Решение:

5𝑥𝑥 + 2𝑥 − 3² = 0,

𝑥₁ = 0, 𝑥₂ = −2, 𝑥₂ = 3.

𝑥₁ ∈ (−3;1), 𝑥₂ ∈ (−3;1), 𝑥₃ ∉ (−3;1).

𝑓 0      = (0 + 2)²(0 − 3)³ = −108,

𝑓 −2      = (−2 + 2)²(−2 − 3)³= 0

𝑓наиб.(𝑥) = 0, 𝑓наим.(𝑥) = −216.

𝑥 ∈ [−3; 1ሿ                              𝑥 ∈ [−3; 1ሿ

𝑥² + 4 функций:  б) 𝑓 𝑥 =  , −3;−1.

𝑥

Решение:

𝑓,

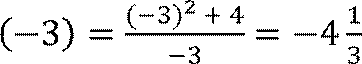(−1)² + 4

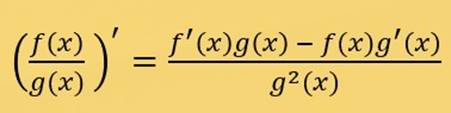
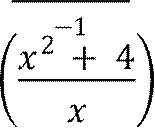𝑓−1 =                   = −5.

′(𝑥) =′ = 2𝑥 ∙ 𝑥 −𝑥2 𝑥2 + 4 =

𝑓

𝑥² − 4

= 𝑥₂ ,

функций:  б) 𝑓

Решение: 𝑥² − 4 ,

𝑥

(𝑥 − 2)(𝑥 + 2)

2 = 0,

𝑥

𝑥₁ = 2, 𝑥₂ = −2,

𝑥² + 4

𝑥 =               , −3;−1.

𝑥

𝑥₁ ∉ (−3; −1), 𝑥₂ ∈ (−3; −1).

𝑓

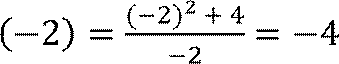
𝑓наиб.(𝑥) = −4, 𝑓наим.(𝑥) = −5.

𝑥 ∈ [−3;−1ሿ          𝑥 ∈ [−3;−1ሿ