


неопределенный интеграл
Определение:
 Если функция 𝑦=𝑓
𝑥 имеет на промежутке I первообразную 𝑦=𝐹
𝑥 , то множество всех первообразных, т.е. множество
функций вида
Если функция 𝑦=𝑓
𝑥 имеет на промежутке I первообразную 𝑦=𝐹
𝑥 , то множество всех первообразных, т.е. множество
функций вида
![]()
![]()
![]() 𝑦=𝐹 𝑥
+𝐶 называют неопределенным интегралом от функции 𝑦=𝑓
𝑥 и обозначают ∫𝑓 𝑥
ⅆ𝑥
𝑦=𝐹 𝑥
+𝐶 называют неопределенным интегралом от функции 𝑦=𝑓
𝑥 и обозначают ∫𝑓 𝑥
ⅆ𝑥
(читают: неопределенныйинтегралэфотиксдэикс).
неопределенный интеграл
Определение: То есть записывают
![]()
![]() ∫
𝒇 𝒙 ⅆ𝒙 = 𝑭
𝒙 + 𝑪
∫
𝒇 𝒙 ⅆ𝒙 = 𝑭
𝒙 + 𝑪
(читают: неопределенный интеграл эф от икс дэ икс).
Где ∫− знак интеграла,
𝑓 𝑥 – подынтегральная функция,
 𝑓 𝑥 ⅆ𝑥
–
подынтегральное выражение,
𝑓 𝑥 ⅆ𝑥
–
подынтегральное выражение,
𝐹 𝑥 – одна из первообразных
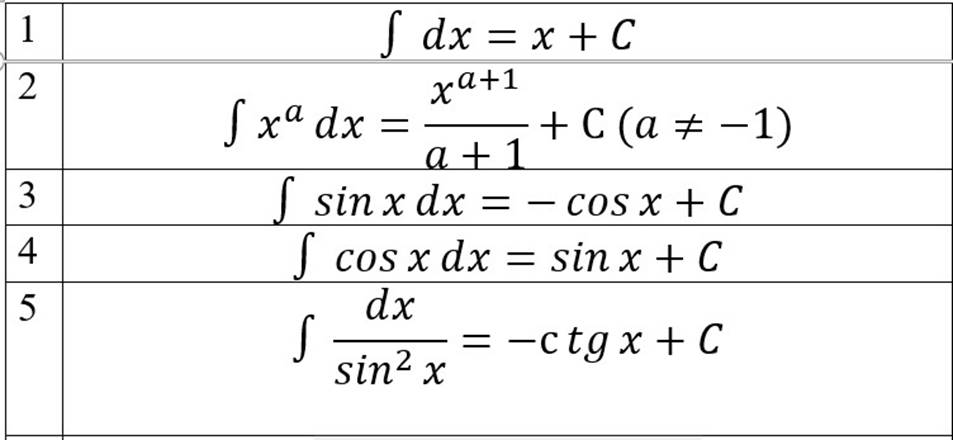
Таблица
неопределённых интегралов:
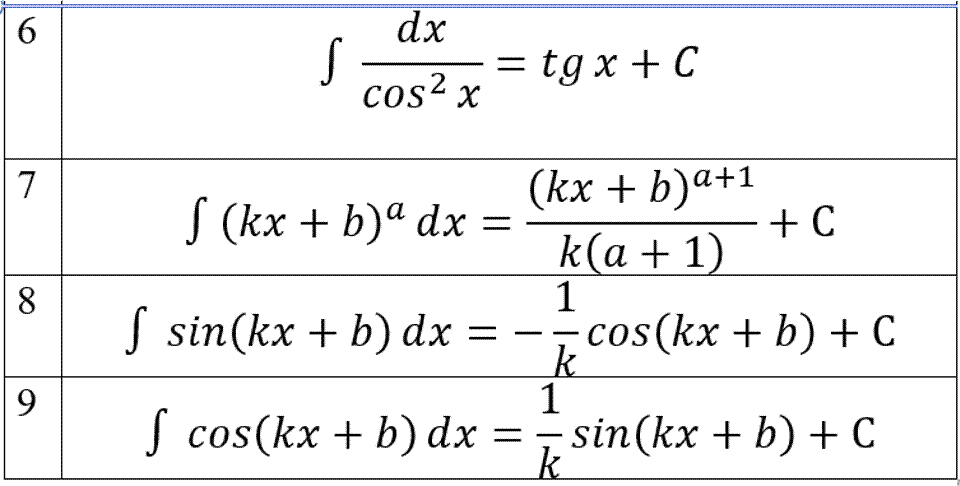
Таблица
неопределённых интегралов:
ПРАВИЛА ИНТЕГРИРОВАНИЯ:
ПРАВИЛО 1.
Интеграл от суммы функций равен сумме интегралов этих функций:
![]()
![]() ∫ 𝒇 𝒙 +
𝒈 𝒙 ⅆ𝒙 = ∫ 𝒇 𝒙 ⅆ𝒙
+ ∫ 𝒈 𝒙 ⅆ𝒙
∫ 𝒇 𝒙 +
𝒈 𝒙 ⅆ𝒙 = ∫ 𝒇 𝒙 ⅆ𝒙
+ ∫ 𝒈 𝒙 ⅆ𝒙
Пример 1:
Вычислить неопределенный интеграл:
∫
![]() 𝑥4 + 𝑐𝑜𝑠𝑥
𝑥4 + 𝑐𝑜𝑠𝑥![]() ⅆ𝑥 =
ⅆ𝑥 =
Пример 1(решение):
Вычислить неопределенный интеграл:
∫
![]() 𝑥4 + 𝑐𝑜𝑠𝑥
𝑥4 + 𝑐𝑜𝑠𝑥![]() ⅆ𝑥 =
ⅆ𝑥 =
Применяя первое правило интегрирования, получим =∫ 𝑥4 ⅆ𝑥 + ∫ cos𝑥 ⅆ𝑥 =
𝑥5
 𝑠𝑖𝑛𝑥
+ 𝐶
𝑠𝑖𝑛𝑥
+ 𝐶
ПРАВИЛА ИНТЕГРИРОВАНИЯ:
ПРАВИЛО 2.
Постоянный множитель можно вынести за знак интеграла:
![]()
![]() ∫
𝒌𝒇 𝒙 ⅆ𝒙 = 𝒌∫ 𝒇 𝒙
ⅆ𝒙
∫
𝒌𝒇 𝒙 ⅆ𝒙 = 𝒌∫ 𝒇 𝒙
ⅆ𝒙
Пример 2:
Вычислить неопределенный интеграл:
න2𝑥3 ⅆ𝑥 =
Пример 2(решение):
Вычислить неопределенный интеграл: න2𝑥3 ⅆ𝑥 =
Воспользовавшись вторым правилом интегрирования, получим
𝑥4 𝑥4
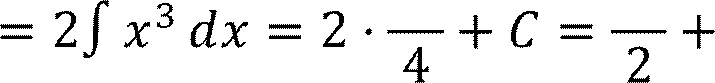 𝐶
𝐶
Пример 3:
Вычислить неопределенный интеграл:
න5𝑠𝑖𝑛𝑥 ⅆ𝑥 =
Пример 3(решение):
Вычислить неопределенный интеграл: න5𝑠𝑖𝑛𝑥 ⅆ𝑥 =
Воспользовавшись вторым правилом интегрирования, получим
= 5∫ sin𝑥ⅆ𝑥 = −5cos𝑥 + 𝐶
ПРАВИЛА ИНТЕГРИРОВАНИЯ:
ПРАВИЛО 3.
![]()
![]() Если ∫
𝒇 𝒙 ⅆ𝒙 = 𝑭 𝒙 + 𝑪, то
Если ∫
𝒇 𝒙 ⅆ𝒙 = 𝑭 𝒙 + 𝑪, то
𝟏
∫ 𝒇![]() 𝒌𝒙
+ 𝒃
𝒌𝒙
+ 𝒃![]() ⅆ𝒙 =
ⅆ𝒙 = ![]() 𝑭
𝑭![]() 𝒌𝒙
+ 𝒃
𝒌𝒙
+ 𝒃![]() + С
+ С
𝒌
Пример 4:
Вычислить неопределенный интеграл:
∫
𝑐𝑜𝑠![]() 3𝑥 + 4
3𝑥 + 4![]() ⅆ𝑥 =
ⅆ𝑥 =
Пример 4(решение):
Вычислить неопределенный
интеграл: ∫ 𝑐𝑜𝑠![]() 3𝑥
+ 4
3𝑥
+ 4![]() ⅆ𝑥 =
ⅆ𝑥 =
Воспользовавшись третьим правилом интегрирования, получим
= ![]() sin
sin![]() 3𝑥
+ 4
3𝑥
+ 4![]() + 𝐶
+ 𝐶
Пример 5:
Вычислить неопределенный интеграл:
∫
![]() 2𝑥 + 1
2𝑥 + 1![]() 4 ⅆ𝑥
=
4 ⅆ𝑥
=
Пример 5(решение):
Вычислить неопределенный интеграл:
∫
![]() 2𝑥 + 1
2𝑥 + 1![]() 4 ⅆ𝑥
=
4 ⅆ𝑥
=
Воспользовавшись третьим правилом интегрирования, получим
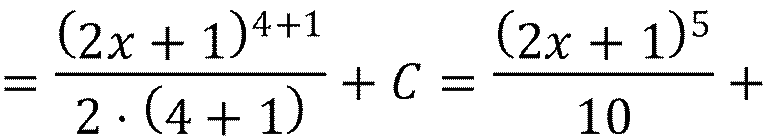 𝐶
𝐶
Пример 6:
Найти неопределённый интеграл: ⅆ𝑥
∫
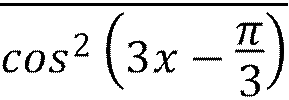
Пример 6(решение):
Найти неопределённый интеграл:
ⅆ𝑥
∫ 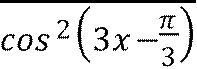
Решение: Воспользовавшись третьим правилом интегрирования и формулой 𝑡𝑔𝑥 + 𝐶, получим:
 𝑐𝑜𝑠
𝑥
𝑐𝑜𝑠
𝑥
![]()
![]()
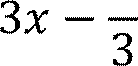 ⅆ𝑥 1𝜋
ⅆ𝑥 1𝜋
∫ 𝜋
= ![]() 3𝑡𝑔
3𝑡𝑔
 𝑐𝑜𝑠2 3𝑥
− 3
𝑐𝑜𝑠2 3𝑥
− 3
Пример 7:
Найти неопределённый интеграл:
∫ ![]() 𝑥
− 2𝑥2 + 5
𝑥
− 2𝑥2 + 5![]() ⅆ𝑥
ⅆ𝑥
Пример 7(решение):
Найти неопределённый интеграл: ∫ ሺ𝑥 − 2𝑥2 + 5ሻ ⅆ𝑥
Решение: Воспользовавшись первым и вторым правилами интегрирования, получим:
∫ ![]() 𝑥
− 2𝑥2 + 5
𝑥
− 2𝑥2 + 5![]() ⅆ𝑥 =
ⅆ𝑥 =
=∫ 𝑥ⅆ𝑥 − 2∫ 𝑥2 ⅆ𝑥 + 5∫ ⅆ𝑥=
= 𝑥![]() 2 −
2 ⋅
2 −
2 ⋅ ![]() 𝑥3 + 5𝑥
+ 𝐶
𝑥3 + 5𝑥
+ 𝐶
2 3
Пример 8:
Найти неопределённый интеграл:
 5
5
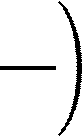 ∫− 𝑥2
ⅆ𝑥
∫− 𝑥2
ⅆ𝑥
Пример 8(решение):
Решение: Преобразуем выражение
 5
5
 ∫− 𝑥2
ⅆ𝑥 =
∫− 𝑥2
ⅆ𝑥 =
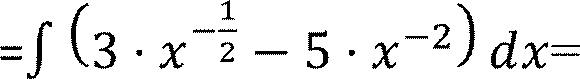
Пример 8(решение):
Воспользовавшись первым и вторым правилами интегрирования, получим:

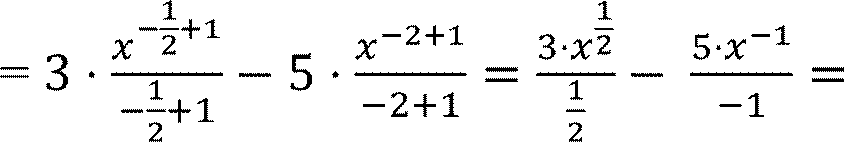
 𝐶
𝐶
𝑥 𝑥
Домашнее задание
Найдите следующие интегралы:
![]() 1.∫
1.∫
![]() 2𝑥3 + 4𝑥
ⅆ𝑥
2𝑥3 + 4𝑥
ⅆ𝑥
2.∫ 𝑥 ⋅ ![]() 𝑥2
+ 4 ⅆ𝑥
𝑥2
+ 4 ⅆ𝑥
3.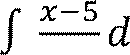 𝑥
𝑥
𝑥
![]() 4.∫
4.∫![]() 2𝑥
𝑥−3𝑥
2𝑥
𝑥−3𝑥![]() ⅆ𝑥
ⅆ𝑥
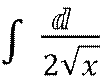 𝑥
𝑥
5.

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.