


![]()
![]()
![]() Вы умеете по заданной
функции находить её производную, знаете, что производная применяется во многих областях знаний. В частности, умея
дифференцировать, по данному закону 𝑦 = 𝑠 𝑡 движения
материальной точки по координатной прямой можно найти закон 𝑦
= 𝑣 𝑡 измерения её скорости, а именно: 𝑣
𝑡 = 𝑠′ 𝑡 .
Вы умеете по заданной
функции находить её производную, знаете, что производная применяется во многих областях знаний. В частности, умея
дифференцировать, по данному закону 𝑦 = 𝑠 𝑡 движения
материальной точки по координатной прямой можно найти закон 𝑦
= 𝑣 𝑡 измерения её скорости, а именно: 𝑣
𝑡 = 𝑠′ 𝑡 .
Нередко в механике приходится решать обратную задачу: находить закон движения по известному закону изменения скорости.
Например, из курса физики вам известен такой факт: если скорость тела
![]()
![]() изменяется по закону 𝑣
𝑡 = 𝑔𝑡 и 𝑠 0 = 0,
то закон его движения задаётся формулой
изменяется по закону 𝑣
𝑡 = 𝑔𝑡 и 𝑠 0 = 0,
то закон его движения задаётся формулой
𝑔𝑡2
![]() 𝑆
𝑡 = .
𝑆
𝑡 = .
2
′
![]()
![]() В
самом деле, 𝑠′ 𝑡 = =
𝑔 𝑡2 ′ =
В
самом деле, 𝑠′ 𝑡 = =
𝑔 𝑡2 ′ = ![]() 𝑔
⋅
2𝑡 = 𝑔𝑡
𝑔
⋅
2𝑡 = 𝑔𝑡
22
Вы знаете, что нахождение производной заданной функции называют дифференцированием. Обратную операцию, т. е. нахождение функции по её производной, называют интегрированием.
Определение: Функция F(x) называется первообразной функции f(x) на некотором промежутке, если для всех х из этого промежутка выполняется равенство F/(x) = f(x).
![]() Пример1:
Доказать,
что функции 𝐹1 = 𝑥3, 𝐹2
= 𝑥3 + 1, 𝐹3 = 𝑥3 −
4 являются
первообразными функции 𝑓 𝑥 = 3𝑥2.
Пример1:
Доказать,
что функции 𝐹1 = 𝑥3, 𝐹2
= 𝑥3 + 1, 𝐹3 = 𝑥3 −
4 являются
первообразными функции 𝑓 𝑥 = 3𝑥2.
Решение: Найдем производные для данных функций:
 𝐹=
3𝑥2;
𝐹=
3𝑥2;
𝐹2′= 3𝑥2 + 0 = 3𝑥2;
𝐹3′= 3𝑥2 − 0 = 3𝑥2
•
![]()
![]() Каждая из них имеет одну
и ту же производную 𝑓 𝑥 =3𝑥2.
Поэтому все функции F1, F2, F3 являются
первообразными функции 𝑓 𝑥 = 3𝑥2.
Каждая из них имеет одну
и ту же производную 𝑓 𝑥 =3𝑥2.
Поэтому все функции F1, F2, F3 являются
первообразными функции 𝑓 𝑥 = 3𝑥2.
•
![]() Понятно, что
каждая из функций 𝐹=𝑥3+𝐶,
где 𝐶-
любое число, является первообразной функции 𝑓 𝑥 = 3𝑥2.
Следовательно
задача нахождения первообразной имеет бесконечно много решений.
Понятно, что
каждая из функций 𝐹=𝑥3+𝐶,
где 𝐶-
любое число, является первообразной функции 𝑓 𝑥 = 3𝑥2.
Следовательно
задача нахождения первообразной имеет бесконечно много решений.
• Задача интегрирования состоит в том, чтобы для заданной функции найти все её первообразные на заданном промежутке.
ОСНОВНОЕ СВОЙСТВО
ПЕРВООБРАЗНОЙ
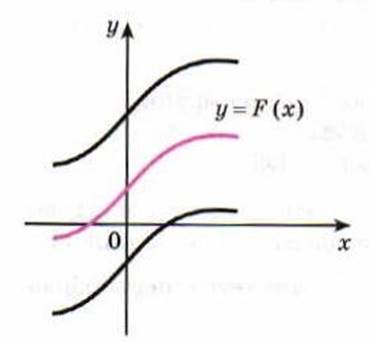 Если функция F(x) является первообразной
функции f(x) на некотором промежутке, то все первообразные функции f(x)
записываются в виде F(x) + C, где С – любое число.
Если функция F(x) является первообразной
функции f(x) на некотором промежутке, то все первообразные функции f(x)
записываются в виде F(x) + C, где С – любое число.
• Запись вида F(x) + C называется общим видом первообразных функции f(x) на некотором промежутке.
• Из основного свойства первообразных следует, что графики любых двух первообразных данной функции можно получить друг из друга параллельным переносом вдоль оси ординат.
 |


ПРАВИЛО 1. Первообразная суммы равна сумме первообразных.
Пример 2: Найти первообразную для функции 𝑦 = 𝑥3 + 𝑐𝑜𝑠 𝑥
![]() 3 является 𝑥4,
первообразной для
3 является 𝑥4,
первообразной для
Решение: Первообразной для 𝑥
4
𝑐𝑜𝑠 𝑥 является 𝑠𝑖𝑛 𝑥.Значит, первообразной для f(x)= 𝑥3 + 𝑐𝑜𝑠 𝑥 будет являться функция
ПРАВИЛО 2. Если F(x) – первообразная для функции f(x), то 𝒌F(x) – первообразная для 𝒌f(x).
Пример 3: Найти первообразную для функции
𝑦 = 7 𝑐𝑜𝑠 𝑥
![]() Решение: Первообразной для
𝑓
𝑥 = 𝑐𝑜𝑠𝑥 является
Решение: Первообразной для
𝑓
𝑥 = 𝑐𝑜𝑠𝑥 является
![]() 𝐹 𝑥 = 𝑠𝑖𝑛
𝑥 . Значит, для функции
𝐹 𝑥 = 𝑠𝑖𝑛
𝑥 . Значит, для функции
![]()
![]() 𝑦 = 7 𝑐𝑜𝑠
𝑥 первообразной будет функция 𝐹
𝑥 = 7 𝑠𝑖𝑛 𝑥 (и
вообще любая функция вида 𝐹 𝑥 = 7 𝑠𝑖𝑛
𝑥 + С).
𝑦 = 7 𝑐𝑜𝑠
𝑥 первообразной будет функция 𝐹
𝑥 = 7 𝑠𝑖𝑛 𝑥 (и
вообще любая функция вида 𝐹 𝑥 = 7 𝑠𝑖𝑛
𝑥 + С).
ПРАВИЛО 2. Если F(x) – первообразная для функции f(x), то 𝒌F(x) – первообразная для 𝒌f(x).
sin 𝑥
Пример 4: Найти
первообразную для функции 𝑦 = ![]() .
.
5
![]()
![]()
![]()
![]()
![]() Решение:
Первообразной
для 𝑓
𝑥 = sin 𝑥 является 𝐹
𝑥 = −cos𝑥 . Значит, для функции 𝑓
𝑥 =
Решение:
Первообразной
для 𝑓
𝑥 = sin 𝑥 является 𝐹
𝑥 = −cos𝑥 . Значит, для функции 𝑓
𝑥 = ![]() 𝑠𝑖𝑛𝑥 первообразной
будет функция 𝐹 𝑥 = −
𝑠𝑖𝑛𝑥 первообразной
будет функция 𝐹 𝑥 = − ![]() 𝑐𝑜𝑠
𝑥(и вообще любая функция вида 𝐹
𝑥 = −
𝑐𝑜𝑠
𝑥(и вообще любая функция вида 𝐹
𝑥 = −![]() 𝑐𝑜𝑠𝑥+С).
𝑐𝑜𝑠𝑥+С).
Пример 5: Найти первообразную для функции 𝑦 = 2𝑥3 − 4𝑥 − 2
![]()
![]() 3 является
𝐹
𝑥 𝑥4
3 является
𝐹
𝑥 𝑥4
![]() Решение: Первообразной
для 𝑓
𝑥 = 2𝑥
Решение: Первообразной
для 𝑓
𝑥 = 2𝑥
𝑥4
![]()
![]() . Первообразной
для функции 𝑓 𝑥 = 4𝑥 является
функция
. Первообразной
для функции 𝑓 𝑥 = 4𝑥 является
функция
2
𝑥2
![]()
![]()
![]()
![]() 𝐹 𝑥
𝐹 𝑥 ![]() .
Первообразной для функции 𝑓 𝑥 = 2 является
𝐹
𝑥 = 2𝑥
.
Используя первое и второе правила нахождения первообразных, получим, что
первообразной для функции 𝑦 = 2𝑥3 −
4𝑥 − 2 является функция 𝐹
𝑥
.
Первообразной для функции 𝑓 𝑥 = 2 является
𝐹
𝑥 = 2𝑥
.
Используя первое и второе правила нахождения первообразных, получим, что
первообразной для функции 𝑦 = 2𝑥3 −
4𝑥 − 2 является функция 𝐹
𝑥 ![]() 𝑥4
𝑥4
𝑥![]() 2 −
2𝑥 =
2 −
2𝑥 = ![]() 𝑥4 −
2𝑥2 − 2𝑥 ( и вообще любая функция
вида
𝑥4 −
2𝑥2 − 2𝑥 ( и вообще любая функция
вида
2 2
![]()
![]() 𝐹
𝑥 = 𝑥4 −
2 2 − 2𝑥 + С).
𝐹
𝑥 = 𝑥4 −
2 2 − 2𝑥 + С).
𝑥
2
![]() Пример
6: Для функции 𝑓 𝑥 = 𝑥
найти
такую первообразную, график которой проходит через точку (2;5).
Пример
6: Для функции 𝑓 𝑥 = 𝑥
найти
такую первообразную, график которой проходит через точку (2;5).
Решение: Все первообразные данной функции находятся по
![]() 𝑥2 формуле
𝐹
𝑥 =
𝑥2 формуле
𝐹
𝑥 = ![]() + 𝐶.
+ 𝐶.
2
𝑥2
Найдём число С,
такое, чтобы график функции у = ![]() + 𝐶
+ 𝐶
2
проходил через точку (2;5). Подставляя 𝑥 = 2, 𝑦 = 5, получаем
22𝑥2
![]() 5 =
5 = ![]() + 𝐶,
откуда
находим 𝐶
= 3. Следовательно,
𝐹
𝑥 =
+ 𝐶,
откуда
находим 𝐶
= 3. Следовательно,
𝐹
𝑥 =
![]() + 3.
+ 3.
22
ПРАВИЛО
3: Если у=F(x) – первообразная для функции у=f(x), то для функции 𝒚
= 𝒇![]() 𝒌𝒙 + 𝒃
𝒌𝒙 + 𝒃![]() является функция
является функция
𝟏
![]() 𝒚
= 𝑭 𝒌𝒙 + 𝒃
𝒚
= 𝑭 𝒌𝒙 + 𝒃![]() .
.
𝒌
![]() Пример 7: Найти
первообразную для функции 𝑓 𝑥 =
Пример 7: Найти
первообразную для функции 𝑓 𝑥 =
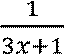 .
.
![]() Решение: Так как для функции 𝑓
𝑥 =
Решение: Так как для функции 𝑓
𝑥 = ![]() 1
1
𝑘𝑥+𝑏
![]() 1 первообразная
равна 𝐹
𝑥 =
1 первообразная
равна 𝐹
𝑥 = ![]() 𝑙𝑛
𝑙𝑛![]() 𝑘𝑥
+ 𝑏
𝑘𝑥
+ 𝑏![]() ,то для функции
,то для функции
𝑘
![]()
![]() 𝑓 𝑥 =
𝑓 𝑥 = 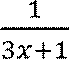 первообразная
равна 𝐹
𝑥 =
первообразная
равна 𝐹
𝑥 = ![]() 𝑙𝑛
𝑙𝑛![]() 3𝑥
+ 1
3𝑥
+ 1![]() .
.
ПРАВИЛО 3: Если у=F(x) – первообразная для функции у=f(x), то
![]() 𝟏 для
функции 𝒚 = 𝒇
𝟏 для
функции 𝒚 = 𝒇![]() 𝒌𝒙
+ 𝒃
𝒌𝒙
+ 𝒃![]() является функция 𝒚
= 𝑭 𝒌𝒙 + 𝒃
является функция 𝒚
= 𝑭 𝒌𝒙 + 𝒃![]() .
.
𝒌
Пример 8: Найти первообразную для функции 𝑓 𝑥 = 2 𝑠𝑖𝑛 3𝑥
![]() Решение: Так
как для функции 𝑓 𝑥 = 𝑠𝑖𝑛
Решение: Так
как для функции 𝑓 𝑥 = 𝑠𝑖𝑛![]() 𝑘𝑥
+ 𝑏 первообразная
𝑘𝑥
+ 𝑏 первообразная
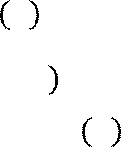
![]() 1 равна 𝐹
𝑥 = −
1 равна 𝐹
𝑥 = − ![]() 𝑐𝑜𝑠
𝑐𝑜𝑠![]() 𝑘𝑥
+ 𝑏
𝑘𝑥
+ 𝑏![]() , то для функции 𝑓
𝑥 = 2 𝑠𝑖𝑛 3𝑥
, то для функции 𝑓
𝑥 = 2 𝑠𝑖𝑛 3𝑥
𝑘
первообразная
равна F(x)= − ![]() 𝑐𝑜𝑠
3𝑥
𝑐𝑜𝑠
3𝑥
ПРАВИЛО 3: Если у=F(x) – первообразная для функции у=f(x), то
![]() 𝟏 для
функции 𝒚 = 𝒇
𝟏 для
функции 𝒚 = 𝒇![]() 𝒌𝒙
+ 𝒃
𝒌𝒙
+ 𝒃![]() является функция 𝒚
= 𝑭 𝒌𝒙 + 𝒃
является функция 𝒚
= 𝑭 𝒌𝒙 + 𝒃![]() .
.
𝒌
Пример 9: Найти
первообразную для функции 𝑓 𝑥 =
𝑐𝑜𝑠![]() 4𝑥 − 3
4𝑥 − 3![]()

![]() Решение: Так как для
функции 𝑓
𝑥 = 𝑐𝑜𝑠
Решение: Так как для
функции 𝑓
𝑥 = 𝑐𝑜𝑠![]() 𝑘𝑥 + 𝑏
первообразная
равна
𝑘𝑥 + 𝑏
первообразная
равна
1
![]()
![]() 𝐹 𝑥 =
𝐹 𝑥 = ![]() 𝑠𝑖𝑛
𝑠𝑖𝑛![]() 𝑘𝑥
+ 𝑏
𝑘𝑥
+ 𝑏![]() , то для функции 𝑓
𝑥 = 𝑐𝑜𝑠
, то для функции 𝑓
𝑥 = 𝑐𝑜𝑠![]() 4𝑥
− 3
4𝑥
− 3![]()
𝑘 первообразная равна
![]() 𝐹
𝑥 =
𝐹
𝑥 = ![]() 𝑠𝑖𝑛
𝑠𝑖𝑛![]() 4𝑥
− 3
4𝑥
− 3![]()
ПРАВИЛО 3: Если у=F(x) – первообразная для функции у=f(x), то
![]() 𝟏 для
функции 𝒚 = 𝒇
𝟏 для
функции 𝒚 = 𝒇![]() 𝒌𝒙
+ 𝒃
𝒌𝒙
+ 𝒃![]() является функция 𝒚
= 𝑭 𝒌𝒙 + 𝒃
является функция 𝒚
= 𝑭 𝒌𝒙 + 𝒃![]() .
.
𝒌
Пример 10:
Найти первообразную для функции 𝑓 𝑥 =
![]() 2𝑥 − 3
2𝑥 − 3![]() 5
5
![]()
![]() Решение: Так как для
функции 𝑓
𝑥 =
Решение: Так как для
функции 𝑓
𝑥 = ![]() 𝑘𝑥 + 𝑏 первообразная
𝑘𝑥 + 𝑏 первообразная
![]()
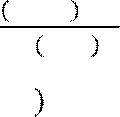 𝑘𝑥+𝑏
𝑎+1
равна
𝐹
𝑥 =, то для функции
𝑘𝑥+𝑏
𝑎+1
равна
𝐹
𝑥 =, то для функции
𝑘 𝛼+1
![]() 𝑓 𝑥 =
𝑓 𝑥 =
![]() 2𝑥 − 3 5 первообразная
равна
2𝑥 − 3 5 первообразная
равна
![]() 𝐹
𝑥
𝐹
𝑥 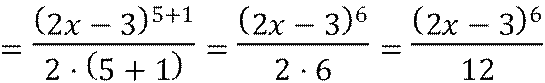
ПРАВИЛО 3: Если у=F(x) – первообразная для функции у=f(x), то
![]() 𝟏 для
функции 𝒚 = 𝒇
𝟏 для
функции 𝒚 = 𝒇![]() 𝒌𝒙
+ 𝒃
𝒌𝒙
+ 𝒃![]() является функция 𝒚
= 𝑭 𝒌𝒙 + 𝒃
является функция 𝒚
= 𝑭 𝒌𝒙 + 𝒃![]() .
.
𝒌
 Пример11:
Найти первообразную для функции 𝑓 𝑥 =
Пример11:
Найти первообразную для функции 𝑓 𝑥 =
Решение: Преобразуем
данную функцию по формуле ![]() 𝑥1𝑛
=𝑥−𝑛
𝑥1𝑛
=𝑥−𝑛
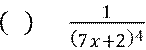 Получим𝑓
𝑥 = =
Получим𝑓
𝑥 = =![]() 7𝑥+2
7𝑥+2![]() −4
−4
![]() Так
как для функции 𝑓 𝑥 = 𝑘𝑥+𝑏
𝑎 первообразная равна 𝐹
𝑥 = 𝑘𝑥+𝑏 𝑎+1,
то
Так
как для функции 𝑓 𝑥 = 𝑘𝑥+𝑏
𝑎 первообразная равна 𝐹
𝑥 = 𝑘𝑥+𝑏 𝑎+1,
то
𝑘 𝛼+1
для функции 𝑓 𝑥 = = 7𝑥+2 −4 первообразная равна
7𝑥+2 −4+1 7𝑥+2 −3 1
 𝐹
𝑥 = 7 −4+1 = −21 =−21 7𝑥+2 3
𝐹
𝑥 = 7 −4+1 = −21 =−21 7𝑥+2 3


Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.