Непрерывность функции

Определение. Функция f(x) непрерывна в точке х₀ тогда и только тогда, когда в этой точке существуют пределы слева и справа, они равны между собой и равны значению функции f(x)   в точке х₀.

                           lim     𝑓 𝑥    = 𝑓(𝑥₀ − 0) =     lim     𝑓 𝑥  = 𝑓(𝑥₀ + 0) = 𝑓(𝑥₀)

𝑥→𝑥0−0𝑥→𝑥0+0

Непрерывность функции

Определение. Если в точке х₀ функция f(x) не является непрерывной, то говорят, что f(x)   имеет разрыв   в этой точке. Точку x₀ называют точкой разрыва функции f(x), причем функция может быть не определена в точке х₀.

 Точки разрыва функции классифицируются в зависимости от того, какое условие непрерывности нарушено.

Устранимый разрыв первого рода

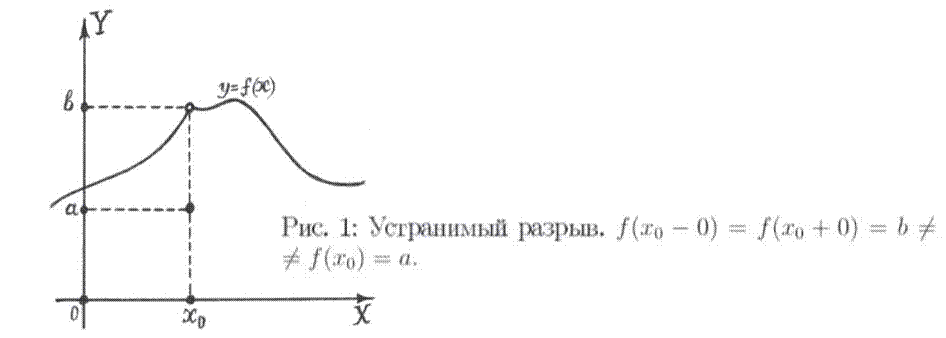𝑥→𝑥0−0𝑥→𝑥0+0

то точка х₀ называется точкой устранимого разрыва функции f(x).

Устранимый разрыв первого рода

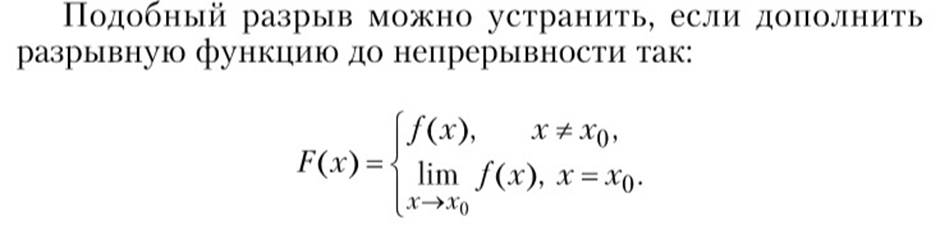
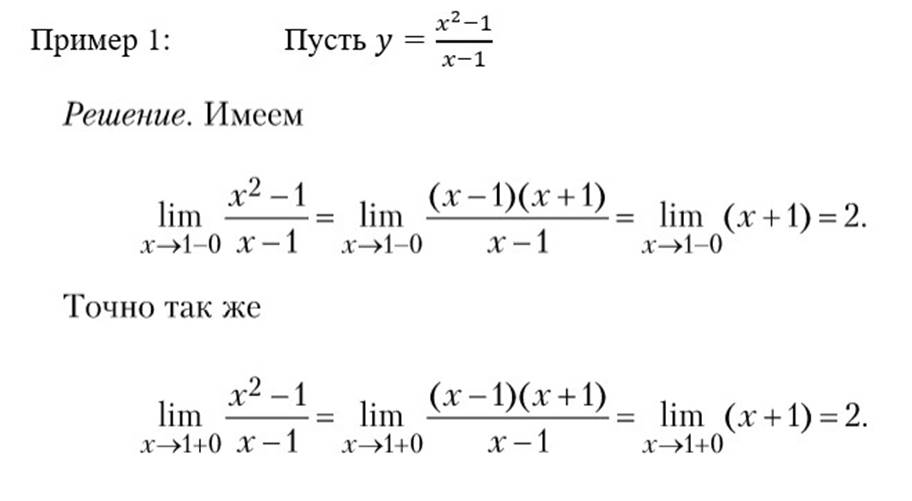
Определение. Если в точке х₀ функция f(x)  имеет  конечные  пределы слева и  справа, но  они не равны между собой

                                                                                               lim      𝑓 𝑥 ≠      lim     𝑓 𝑥

𝑥→𝑥0−0𝑥→𝑥0+0

то точка х₀ называется точкой неустранимого разрыва  первого рода, или разрыва с конечным скачком  функции. (При этом безразлично, совпадает или нет f(x₀) c одним из односторонних пределов.)

Разрыв второго рода

Разрыв второго рода

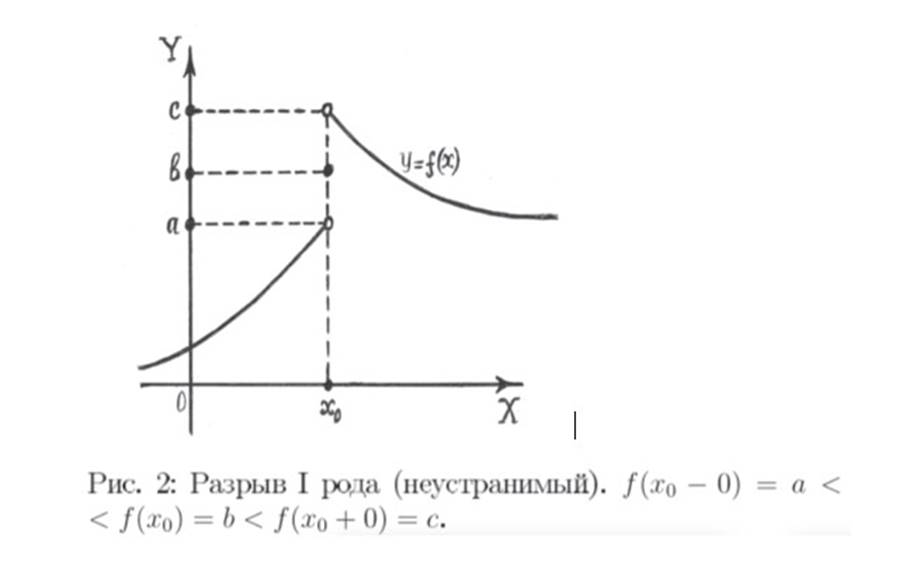
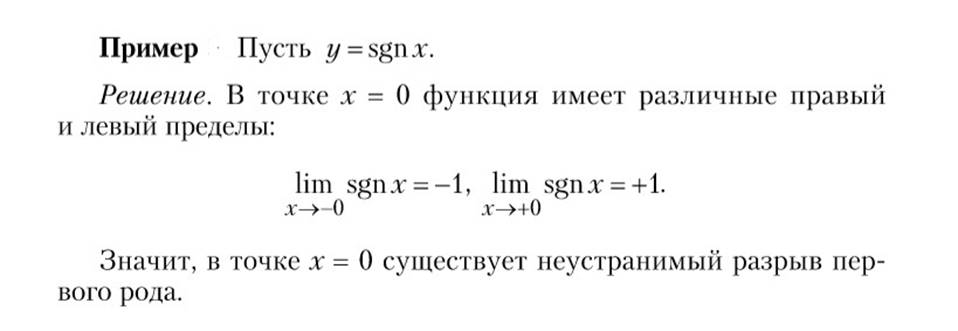
Исследуйте функции на непрерывность.

Классифицируйте точки разрыва если они есть.

2𝑥² − 1; при 𝑥 < 1

•     𝑦 = ൞−𝑥; при 1 ≤ 𝑥 < 3

𝑥 − 3; при 𝑥 ≥ 3

𝑥+1

•     𝑦 =

𝑥+2

−𝑥² − 2𝑥; при − 4 ≤ 𝑥 < 0

•     𝑦 ₌2𝑥; при 0 ≤ 𝑥 < 2

2

 ; при 2 ≤ 𝑥 ≤ 4

𝑥

𝑥² + 2𝑥 − 4; при − 4 ≤ 𝑥 < 3

•     𝑦 = ൞     𝑥 − 2; при 𝑥 ≥ 3

𝑥 + 7; при 𝑥 < −4