Презентация к занятию по теме: "Понятие предела числовой последовательности".

Понятие числовой последовательности

Рассмотрим ряд натуральных чисел N:

1, 2, 3, …, n – 1, n, п + 1, …

Функцию y = f(x), x  N называют функцией натурального аргумента или числовой    последовательностью   и обозначают:

  y = f(n) или у₁ , y₁ , …, y_n , … или {у_n }.

Величина    у_n называется общим   членом последовательности.

Примеры числовых последовательностей:

•   1, 2, 3, 4, 5, 6, … - последовательность натуральных чисел;

•   2, 4, 6, 8, 10, … - последовательность четных чисел;

•   19, 38, 57, 76, 95, …- последовательность двузначных чисел, кратных 19;

•   -1, -2,    -3,    -4,    -5,…     -   последовательность отрицательных целых чисел.

Способы задания последовательностей:

1.Перечислением членов последовательности (словесно).

2.Заданием аналитической формулы.

3.Заданием рекуррентной формулы.

Словесное задание последовательности:

     Последовательности    можно     задавать различными способами, например словесно, когда правило     задания    последовательности     описано словами, без указания формулы. Так словесно задается последовательность простых чисел:

2,3,5,7,11,13,17,19,23,29, … .

Аналитическое задание последовательности:

Последовательность задана аналитически, если указана формула ее n-го члена.

Примеры:

•    𝑦_𝑛 = 𝑛².Это аналитическое задание последовательности

1, 4, 9, 16, …, 𝒏^𝟐, … .

•    𝑦_𝑛 = С. Здесь речь идет о последовательности С, С, С, С, С, … .

Такую последовательность называют постоянной ( или стационарной).

Рекуррентный способ задания

Рекуррентный    способ    задания последовательности состоит в том, что указывают правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены.

Примеры:

•    Арифметическая прогрессия – это числовая последовательность 𝑎_𝑛 , заданная рекуррентно соотношениями:

                                                                         𝒂𝟏 = 𝒂,           𝒂𝒏+𝟏 = 𝒂𝒏 + 𝒅

( 𝑎 и 𝑑 –   заданные    числа,     𝑑   –   разность арифметической прогрессии).

Рекуррентный способ задания

•    Геометрическая прогрессия  - это числовая последовательность 𝑏_𝑛, заданная рекуррентно соотношениями:

                                                                   𝒃_𝟏 = 𝒃,           𝒃_𝒏+𝟏 = 𝒃_𝒏 ∙ 𝒒

( 𝑏 и 𝑞 − за данные числа, 𝑏 ≠ 0, 𝑞 ≠ 0; 𝑞 – знаменатель геометрической прогрессии).

СВОЙСТВА ЧИСЛОВЫХ

ПОСЛЕДОВАТЕЛЬНОСТЕЙ

Числовая  последовательность – частный случай числовой функции, а потому некоторые свойства функций можно перенести и на последовательности.

Ограниченность числовой последовательности.

Последовательность {у_n} называют ограниченной сверху, если существует такое число M, что для любого n∈𝐍 выполняется неравенство у_n ≤ M.

   Иными    словами, последовательность {у_n}    называют ограниченной      сверху,     если    все    ее члены не больше некоторого числа.

Число М называют верхней границей последовательности.

Пример: -1, -4, -9, -16,  - 25,…, -n² , … - ограничена сверху; в качестве верхней границы можно взять  число -1.

Ограниченность числовой последовательности.

Последовательность {у_n} ограниченна снизу, если существует такое  число m, что для любого n∈𝑵 выполняется неравенство у_n ≥ m.

Иными    словами, последовательность    {у_n}     называют ограниченной снизу, если все ее члены не меньше некоторого числа.

Число m называют нижней границей последовательности.

Пример: 1, 4, 9, 16, …, n² , … - ограничена снизу; в качестве нижней границы можно взять  число 1( или любое число, которое меньше, чем 1).

Ограниченность числовой последовательности.

Если последовательность ограничена и сверху и снизу, то ее называют ограниченной последовательностью.

𝟏 𝟏 𝟏 𝟏 Пример:      1, , , , … ,  , … .

                                                                                      𝟐 𝟑 𝟒             𝒏

В качестве верхней границы можно взять 1, в качестве нижней 0.

Возрастание и убывание числовой последовательности.

Последовательность {у_n} называют возрастающей последовательностью, если каждый ее член больше

предыдущего:      у₁ < y₂ < y₃ < y₄ < … < y_n < y_n+1 < …

Пример: 1, 3, 5, 7, 9, 2n – 1, … - возрастающая последовательность.

Последовательность {у_n} называют убывающей последовательностью, если каждый ее член меньше

предыдущего:        у₁ > y₂ > y₃ > y₄ > … > y_n > y_n+1 > …

Пример:   1,   1/3,      1/5,      1/7,      1/(2п   –    1), … -     убывающая последовательность.

Возрастающие    и    убывающие последовательности       называют монотонными.

последовательности.

Рассмотрим две числовые последовательности 𝑦_𝑛 и 𝑥_𝑛.

𝑥_𝑛: 1,  , ,  , … , _𝑛¹ , … .

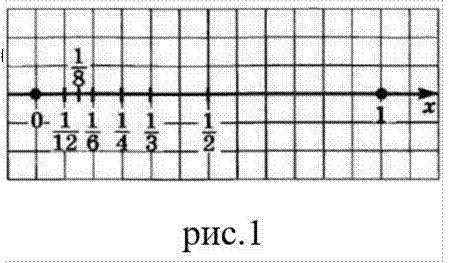
Изобразим  члены этих последовательностей точками на координатной прямой

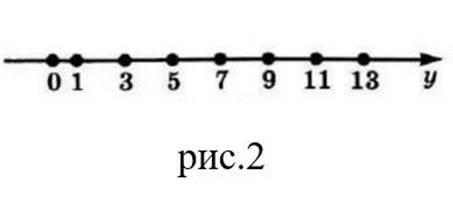
последовательности.

•    Замечаем, что члены последовательности 𝑥_𝑛 как бы « сгущаются» около точки 0, а у последовательности

𝑦_𝑛 такой « точки сгущения»  нет. В подобных случаях  математики говорят так:  последовательность 𝑥_𝑛 сходится, а последовательность 𝑦_𝑛  расходится.

•    Математики не используют  слова «точка сгущения для членов заданной последовательности» они предпочитают использовать термин «предел последовательности».

последовательности.

Определение: Число 𝒂 называется пределом последовательности 𝒙_𝒏, если для любого 𝜺 > 𝟎 все члены последовательности 𝒙_𝒏 , лежат в 𝜺 - окрестности (𝒂 − 𝜺, 𝒂 + 𝜺) точки 𝒂, т.е. найдется такое натуральное число N, что при n>N будет выполнено неравенство 𝒙_𝒏 − 𝒂 < 𝜺

Если  последовательность 𝒙_𝒏 имеет пределом число 𝒂, то пишут lim 𝒙_𝒏 = 𝒂

𝑛→∞

Теорема о пределах

Если 𝒍𝒊𝒎 𝒙_𝒏 = 𝒃,   𝒍𝒊𝒎 𝒚_𝒏 = 𝒄, то

                               𝒏→∞                          𝒏→∞

1)            Предел суммы равен сумме пределов:

𝒍𝒊𝒎( 𝒙_𝒏 + 𝒚_𝒏) = 𝒃 + 𝒄

𝒏→∞

2)            Предел произведения равен произведению пределов: 𝒍𝒊𝒎( 𝒙_𝒏𝒚_𝒏) = 𝒃𝒄

𝒏→∞

3)            Предел частного равен частному пределов:

𝒍𝒊𝒎( 𝒙^𝒏) = ^𝒃 , если   с ≠ 𝟎

                                                                                                     𝒏→∞ 𝒚_𝒏                𝒄

4)            Постоянный множитель можно вынести за знак предела: 𝒍𝒊𝒎(𝒌 𝒙_𝒏) = 𝒌𝒃

𝒏→∞

пределов последовательностей:

пределов последовательностей:

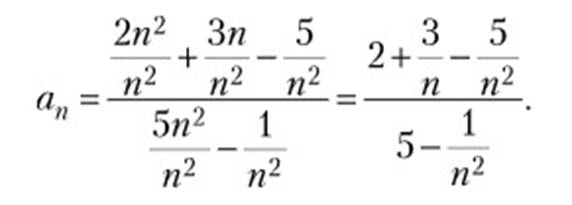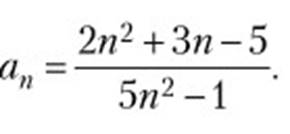
Решение:  Разделим и числитель, и знаменатель на переменную n в наивысшей степени, в которой она входит в данную дробь (в данном случае делим на n²):

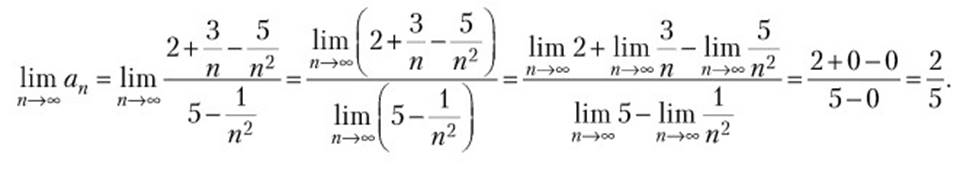
пределов последовательностей: