Презентация 1 Подготовкак ЕГЭ Задание 14

Консультационный Консультационный центр по подготовке центр по подготовке выпускников к выпускников к Государственной Государственной (итоговой) (итоговой) аттестации аттестации

Консультационный центр по подготовке выпускников к  Государственной (итоговой) аттестации С2С2 МАУ ЗАТО Северск «Ресурсный центр образования»

Консультационный центр по подготовке выпускников к  Государственной (итоговой) аттестации С2С2 Решение задач ЕГЭ. Часть С2 Задача 1: Нахождение расстояния от точки до плоскости  ( в треугольной призме); Задача 2: Нахождение расстояния от точки до плоскости (в кубе); Задача 3: Нахождение угла между прямой и плоскостью  ( в прямоугольном параллелепипеде) ; Задача 4: Нахождение тангенса угла между прямой и плоскостью ( в прямоугольном параллелепипеде); Задача 5: Нахождение угла между прямой и плоскостью ( в правильной треугольной призме); Задача 6: Нахождение тангенса угла между прямой и плоскостью ( в кубе); Задача 7: Нахождение синуса угла между прямой и плоскостью ( в тетраэдре). МАУ ЗАТО Северск «Ресурсный центр образования»

СС22   Основанием прямой призмы ABCA1B1C1 является равнобедренный       треугольник ABC, AB = АC = 5, BC = 6. Высота призмы равна 3. Найдите  расстояние от середины ребра B1C1 до плоскости BCA1. NN NKNK – искомое расстояние  – искомое расстояние СС11 44 33 АА11 KK 5 5 АА 5 NN 44 ВВ11 3 33 СС 33 6 DD ВВ АА11 KK DD 55 ANDS 634 1 2 1 2  55 AD  NK * 2 66 S AND 1 2 12  6 NK 5 NK5 : 5 4,2NK

Дан куб ABCDA1B1C1D1 с ребром  1. Найдите расстояние от точки       А  до  плоскости A1 BТ,  где Т ­  середина отрезка AD.  Опустить перпендикуляр из точки на плоскость не всегда просто.  Применим другой способ для вычисления расстояния от точки  А  до   плоскости A1 BТ. Найдем AO, выразив два раза объем пирамиды  ABTA1 с основанием АВТ. :  2 ;1 Из 2 TB AA 1 D1 С1 В1 AB ; 2 2 ; А1 2 ;1 11 А O 11 22 T 22 D 55 22 11 11 В Из BA 1 BA 1 BA 1 BA 1 BA 1 2  ABA 1 2  2 AB  2 1  ;2   .2 2 ;2  : ATB   2 AT 2   1   2   1 4 5 4  1  ; ; 2 TB 2 TB С TB TB  5 2 .

T H 22 55 22 22 22 A1 D1 С1 В1 O 11 22 T 22 D 55 22 11 С 11 В А1 11 А 55 22 B Из  2 TA 1    5 2 2 HT :1HTA   2 2 HT 2 HT    3 4  ; HT  3 4 ; HT  3 2 . 2 ;  HA 1    STBA 2 2 2 ;     1 1 2 1 2 TBAS 1 1 THBA 1  ; TBAS 2 3 2 ; 6 4 .

V пир .  1 3 S осн .  H ; пр  S тр . . D1 С1 1 2 ba ; 1 12 В1 V ABTA 1  S TBA 1 3 1 1 2 2 ABTAV 1 1 ABTAV ;1 1 12 1 1 3 . 6 4  ; AO 1 TBAS 1 3 TBA 1 S      Найдем AO, выразив два раза объем  пирамиды ABTA1 с основанием АВТ. V ABTA 1   AА 1 ; А1 11 А O 11 22 T 22 D 55 22 11 1 12  1 3 6 4 AO ; 12 С 11 В 1 AO 6 ;   6 6 1AO 6 6AO 6

В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол  между прямой A1B и плоскостью AA1C, если AA1 = 6, AB = 8, BC = 8.  Угол между наклонной и  Угол между наклонной и  плоскостью – это угол между  плоскостью – это угол между  наклонной и её проекцией на эту  наклонной и её проекцией на эту  плоскость.  плоскость.  C1 B1 D1 66 66 D A1  н н а а к к л л о о н н н н 1010 я я и и ц ц к к е е о о р р п п а а я я B 88 C 22 44 A O 88 AB 11 2 ; sin Из  :1BОО ВО 1BА ; sin   sin   ; 24 10 22 5 2 ;  arcsin 22 5 . :  2 ;8 2 2  BABИз 1 1 2  2 BA BB 1 1  2 BA 6 1  BA ;100 1  BA ;10 1  BA .10 1  Из ABD :   2 2 BD AB  2 2 BD 8 ;8  2 BD ;82  BD ;28  BD Тогда 2 2 .28 .24BO DA

В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого  AB = 4, BC = 6, CC1 = 4, найдите тангенс угла между плоскостью  ABC и прямой EF, проходящей через середины ребер AA1 и C1D1.  D1 1 1 к к е е о о 22 22 F 0 0 ц ц и и я я  р р п п наклонная наклонная D А1 22 Е А 44 С1 44 С В1 66 66 В E    А1 ,            , F    F 3. Искомый угол EFA1. EF    А1F 2 2 1. Угол между прямой EF и  плоскостью АВС равен углу между  EF и плоскостью А1В1С1, т.к. эти  Находим тангенс угла EFAEFA11. Это  . Это  Находим тангенс угла  плоскости параллельны. отношение противолежащего  отношение противолежащего  2. Угол между прямой и  катета к прилежащему катету, т.е.  катета к прилежащему катету, т.е.   EAEA11  к к FAFA11.. плоскостью равен углу между  данной прямой и её проекцией на  плоскость.  Из     FEA1 FADИз 1 1 EA 2 2  FA FD 1 1 1 FA  2 2 FA 1 1  2  FA ;40  10 1  FA 10 1  FA 2 10 1 :  2 ;6 ;40 .10 t g t g AD 11 g  t 10 10 2 ;  2

Точка М – середина стороны ВС основания АСВ правильной  призмы АВСА1В1С1. Боковое ребро призмы равно       , а сторона  основания равна 12. Найти синус угла между прямой В1М и  плоскостью боковой грани ABB1A1.       39  2 BB 1  2 39  Из MB 1 MB 1 MB 1 MB 1 MB 1  2 MBB 1  MB : 2 2 2 2  6  ;75  ;325  .35 Из  1HMB : sin   Из  MBH ; sin 60 0  : MH MB ; ; 3 2  MH  ; MH 6 36 2 ; MH  .33 MH MB 1 33 35 ; ; sin  3 5 C1 A1 C 1212 M M B1  ная 33 ная 55 н н о о накл накл я я и и ц ц к к е е о о р р п п 66 66 3333 H ?? 1212 39 B 606000 B 606000 H A B1     B1, M     H, MB1     B1H sin  

В кубе ABCDA1B1C1D1 найдите тангенс угла между прямой АА1 и  плоскостью ВС1D.  Заменим заданную прямую АА1 на параллельную прямую СС1. Угол  между АА1 и плоскостью ВС1D равен углу между параллельной  прямой СС1 и плоскостью ВС1D.   Прямая СС1 является наклонной к плоскости ВС1D. Найдем проекцию  С1     С1, СС1 на плоскость ВС1D.  СC1     C1K,  С     K, А1 А D1 С1 В1 K  проекция проекция 11 н н а а к к л л о о н н н н а а я я 2 BC tg  1ОСС : 2 Для нахождения          более  1KCС удобен              , а не               . Из AC AC AC AC AC   ABC  2 AB  2 1  ;2   ; Из   2 ;1 :1OCC tg ; 2 2 ; С D OC CC 1 2 2 Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1» Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1» 22 22   ;2   .2 tg 11 11 О В

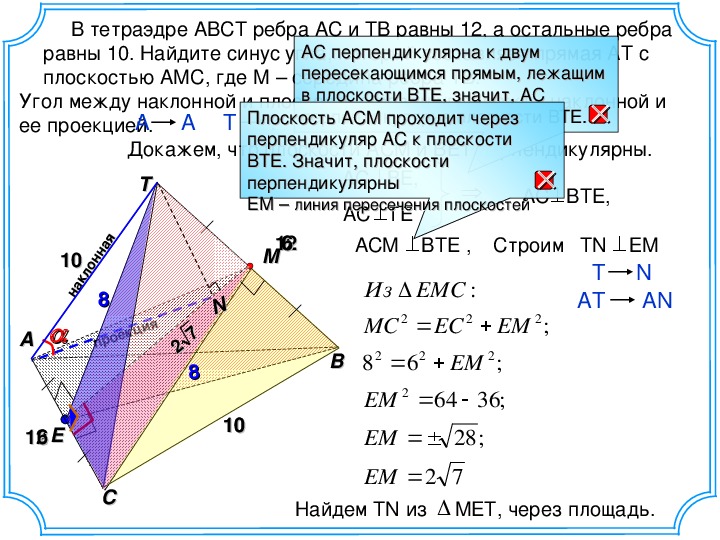
В тетраэдре AВСT ребра AC и TB равны 12, а остальные ребра  равны 10. Найдите синус угла, который составляет прямая АТ с  плоскостью АМС, где М – середина ребра ТВ.  Угол между наклонной и плоскостью равен углу между наклонной и  ее проекцией.   A     A T     ? Докажем, что плоскости ACM и BET перпендикулярны.  TT AC AC перпендикулярна к двум  перпендикулярна к двум  пересекающимся прямым, лежащим  пересекающимся прямым, лежащим  в плоскости BTEBTE, значит,  , значит, ACAC   в плоскости  перпендикулярна плоскости BTE.BTE. перпендикулярна плоскости  Плоскость АCM CM проходит через  проходит через  Плоскость А перпендикуляр ACAC к плоскости   к плоскости  перпендикуляр  ВВTETE..  Значит, плоскости  Значит, плоскости    AC   ВE, перпендикулярны перпендикулярны ЕМЕМ  ––  линия пересечения плоскостей   AC   TE    линия пересечения плоскостей               AC   BTE,  АCM    ВTE , Строим  1212 6666 MM     ТN    ЕМ  T     N   AT      AN 2 ; Найдем TN из     MET, через площадь.   1010 наклонная наклонная  88 о о р р п п AA 1212 6666 EE CC я я к ц и к ц и е е NN 22 77 88 1010 1010 BB : 2  2 EM EM ; ;36  Из 2 MC 2 8 EM EM EM EMC  EC  2 6  2 64   72  ;28

TN    AMC    Найдем TN из     MET через площадь.   TM перпендикуляр к плоскости AMC,  значит, TM будет перпендикулярен  TEMT к любой прямой, лежащей в этой   плоскости.  ab 1  TM    AN S 2 1  2 S 1 2 aah 24 72 MM TT 66 NN 772424 77 77 22 88 1010 1010 88  AA 66 EE 66 CC EM  TN SMTE  SMTE 1 1 MTES 68 2 2 Мы знаем гипотенузу и  Мы знаем гипотенузу и   24 72 противолежащий катет  противолежащий катет  24MTES треугольника  АМТ, значит,  АМТ, значит,  треугольника  вычислим отношение синус.  вычислим отношение синус.  24 24TN 7 24TN 7 TN 7   88 sin  10: 1 2 E E BB 66 TN 7 7 7 7 TNsin T T AT 66 24 7 N M M 24 7  107 12 7 35  7722 sin  sin

Консультационный центр по подготовке выпускников к  Государственной (итоговой) аттестации С2С2 Используемые ресурсы: Используемые ресурсы: •Смирнов В.А., Семенов А.А., Ященко И.В. ЕГЭ- Смирнов В.А., Семенов А.А., Ященко И.В. ЕГЭ- 2013. Математика. Задача С2. Геометрия. 2013. Математика. Задача С2. Геометрия. Стереометрия. Рабочая тетрадь. Издательство Стереометрия. Рабочая тетрадь. Издательство МЦНИО. 2013г.; МЦНИО. 2013г.; •Тексты задач Стат Град и ЕГЭ- сайт Тексты задач Стат Град и ЕГЭ- сайт Александра Ларина. httphttp://://alexlarin Александра Ларина. html html •Сайт ЕГЭ-тренер, видеоуроки Ольги Сайт ЕГЭ-тренер, видеоуроки Ольги Себедаш. httphttp://://wwwwww..egetrener egetrener..ruru//view view Себедаш. zadachi=C2 zadachi=C2 alexlarin//netnet//egeege11.11. МАУ ЗАТО Северск «Ресурсный центр образования»