Приемы активизации творческой деятельности учащихся на уроках математики

Приемы активизации творческой деятельности учащихся на уроках математики

Учитель математики МБОУ БГО СОШ №5,  Хоршева Татьяна Николаевна

Одним из приемов активизации творческой деятельности школьников является использование исторического материала. Школьников можно включать в поиск новых способов решения интересных исторических задач. Через обзоры жизни и деятельности великих математиков школьников можно познакомить с самим понятием творчества, с творчеством в науке. С помощью исторического материала можно дать возможность ученикам самостоятельно приходить к формулировкам теорем, как бы вновь открывая их, давать ученикам искать их доказательства, побуждать в учениках самостоятельно искать любопытные факты истории, связанные с математическими терминами и открытиями. Применение исторического материала на уроках расширяет кругозор и увеличивает интеллектуальный ресурс школьников, а это, в свою очередь способствует и развитию творческих способностей.

Например, в 8 классе перед тем, как познакомить учащихся с новым видом четырехугольника – ромбом, можно показать альбомный лист, с небольшим ромбом красного цвета и спросить, что, по их мнению, здесь изображено. Среди всех вариантов выделяются два: это ромб и это игральная карта (туз бубновой масти). Ассоциации школьников не случайны. «Ромб» латинская норма греческого слова «ромбос», означающего бубен. Раньше бубны имели форму ромба. При изучении новых математических терминов можно предложить школьникам найти историю их возникновения. Например, «линия» происходит от латинского слова «линеа», образовавшегося от слова «linum», что означает лен, льняная нить, шнур, веревка. «Трапеция» латинская форма слова «трапедзион» столик.

При изучении темы «Геометрическая прогрессия» в 9 классе школьникам можно рассказать легенду об изобретателе шахмат и предложить подумать над задачей о зернах и шахматной доске.

Математики прошлого были творческими людьми. Философом и поэтом, классиком персидской и таджикской литературы был известный математик Омар Хайям. Математик и логик Чарлз Л.Джонсон под псевдонимом Льюис Кэрролл стал широко известен как автор сказки «Приключения Алисы в стране чудес». Из рассказов биографов известно, что королева Виктория, после прочтения книги, пожелала прочитать все произведения автора и была удивлена, увидев стопку книг по математике.

Еще один прием. Школьникам предлагаются портреты математиков. Необходимо ответить на вопрос и предъявить портрет ученого.

1.    Основоположник геометрии. Наши учебники геометрии содержат основные понятия, сформулированные этим древнегреческим учёным. (Евклид)

2.    Русский математик, основавший свою, отличную от евклидовой, геометрию. (Николай Лобачевский)

3.    Кому принадлежат слова «Математика – царица всех наук, арифметика – царица математики»? (Фридрих Карл Гаусс)

4.    Кому принадлежат эти строки: «Математику уже затем учить надо, что она ум в порядок приводит»? (Михаилу Ломоносову)

5.    Кто из великих воскликнул: «Дайте мне точку опоры, и я переверну землю»? (Архимед)

6.    Этот ученый ослеп, но целых 20 лет он работал, диктуя своим ученикам, оставил после себя 200 работ. (Леонард Эйлер)

Исторические сведения служат для развития творческих способностей школьников, так как включение сведений о творчестве крупных ученых, о том, как они приходили к постановке своих исследований, как находили метод решения, как формулировали окончательный результат, позволяет создать творческую атмосферу на уроках, помогает понять, что в творчестве нет ничего необычного, но цели достигаются в результате упорного труда.

Для развития творческого мышления применяются математические софизмы. Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.

При разборе математических софизмов выделяются основные ошибки, скрытые в нем:

-     деление на 0;

-     неправильные выводы из равенства дробей;

-     неправильное извлечение квадратного корня из квадрата выражения;

-     нарушения правила действий с именованными величинами;

-     неравносильный переход от одного неравенства к другому;

-     выводы и вычисления по неверно построенным чертежам.

Например, при изучении темы «Арифметический квадратный корень» учащимся можно предложить софизм «Все числа равны между собой».

Возьмем два любых числа и, где и запишем для них очевидное тождество

Свернув левую и правую часть, получим

.

Извлекая из обеих частей равенства квадратный корень получим

,

Учащимся предлагается опровергнуть или согласиться с этим утверждением.

Учащиеся изучили определение квадратного корня: арифметическим квадратным корнем из неотрицательного числа  называется такое неотрицательное число, квадрат которого равен .

.

Очевидно, что в софизме не учитывается свойство арифметического квадратного корня

При работе с данным софизмом у учащихся формируется умение проводить элементарные исследования и, как следствие, формируются такие качества, как умение целенаправленно наблюдать (необходимо заметить в рассуждениях, что даны два любые числа), сравнивать, выдвигать или опровергать гипотезы, обобщать. Развивается умение анализировать информацию, умение выстраивать логику рассуждений.

При выполнении упражнения задача учителя следить за грамотностью математической речи, точным воспроизведением определений.

Еще один софизм «Неравные числа равны», который можно предложить школьникам в начале урока из раздела «Преобразование алгебраических выражений».

Возьмём два произвольных числа a и b, неравных между собой. Пусть их разность равна c.

Умножим обе части этого равенства на , получим

Раскроем скобки и преобразуем, получим

,

Вынесем в обеих частях равенства за скобки общий множитель

Откуда, если обе части равенства разделить на , то получим

.

Вывод: два неравных между собой числа равны.

Учащимся предлагается найти ошибку в рассуждениях.

В последнем переходе от равенства  к равенству спрятана ошибка. Действительно, по условию разность двух произвольных чисел aи b равна c: . Тогда данный переход осуществляется путем деления на обеих частей равенства на равное нулю число. Здесь мы имеем деление нуля на нуль, которое не имеет смысла, поскольку равенство выполняется при любых aи b. Значит вывод, сделанный в софизме неверен.

При работе с этим упражнением у учащихся формируется умение анализировать информацию, формулировать собственное мнение в устной форме, выстраивать логику рассуждений.

При изучении темы «Числовые неравенства» можно предложить учащимся софизм «».

Возьмем очевидное неравенство . К обеим частям прибавим число  - 8. Получим , или . Умножим левую и правую часть неравенства на -4 получим или

Школьникам предлагается найти ошибку в приведенных рассуждениях. Здесь спрятана ошибка: при умножении левой и правой части неравенства на одно и тоже отрицательное число знак неравенства меняется на противоположный, в рассуждениях знак не поменялся.

При выполнении этого устного упражнения формируется умение критически относится к информации, сопоставлять ее с информацией из различных источников и имеющимся жизненным опытом.

Большой простор для творческой деятельности школьников открывает применение приемов ТРКМ.

Прием технологии развития критического мышления “Ромашка Блума”. «Ромашка» состоит из шести лепестков, каждый из которых содержит определенный тип вопроса. Таким образом, шесть лепестков - шесть вопросов:

1.         Простые вопросы — вопросы, отвечая на которые, нужно назвать какие-то факты, вспомнить и воспроизвести определенную информацию: "Что?", "Когда?", "Где?", "Как?".

Простой вопрос. Назовите формулу для вычисления площади прямоугольника. Или. Какие числа делятся на 2?

2.         Уточняющие вопросы. Такие вопросы обычно начинаются со слов: "То есть ты говоришь, что…?", "Если я правильно понял, то …?", "Я могу ошибаться, но, по-моему, вы сказали о …?",

Уточняющий вопрос. Правильно ли я понял, площадь прямоугольника равна квадрату одной из сторон? Или.Правильно ли я понял, что на 2 делятся числа оканчивающиеся 2?

Целью этих вопросов является предоставление учащемуся возможностей для обратной связи относительно того, что он только что сказал. Иногда их задают с целью получения информации, отсутствующей в сообщении, но подразумевающейся.

3.         Интерпретационные (объясняющие) вопросы. Обычно начинаются со слова "Почему?" и направлены на установление причинно-следственных связей.

Объясняющий вопрос. Для чего нужно знать свойства площадей?Или. Почему сумма двух нечетных чисел является четным числом?

Если ответ на этот вопрос известен, он из интерпретационного "превращается" в простой. Следовательно, данный тип вопроса "срабатывает" тогда, когда в ответе присутствует элемент самостоятельности.

4.         Творческие вопросы. Данный тип вопроса чаще всего содержит частицу "бы", элементы условности, предположения, прогноза: "Что изменилось бы ...", "Что будет, если ...?", 

Творческий вопрос. Фермер решил увеличить площадь земельного участка квадратной формы, увеличив при этом сторону в 2 раза. Во сколько раз увеличиться площадь этого участка?Или. Что было бы если бы не было признаков делимости?

5.         Оценочные вопросы. Эти вопросы направлены на выяснение критериев оценки тех или иных событий, явлений, фактов. "Почему что-то хорошо, а что-то плохо?", "Чем один урок отличается от другого?",

Оценочный вопрос. Почему для хранения вычисления площадей используют формулы?

6.         Практические вопросы. Данный тип вопроса направлен на установление взаимосвязи между теорией и практикой: «Как можно применить ...?», «Что можно сделать из ...?», «Где вы в обычной жизни можете наблюдать ...?»,

Практический вопрос. Начертите квадрат и прямоугольник имеющие одинаковые площади. Или. Делится ли число 2019 на 2?

Далее школьникам предлагается составить вопросы по изученному материалу, при этом они пользуются опорным конспектом.

Пример применения приема «Ромашка Блума» на уроке алгебры в 7 классе.

Простой вопрос. Что называется корнем уравнения?

Уточняющий вопрос. Объясните, как проверить, является ли число корнем уравнения.

Оценочный вопрос. Как вы думаете, существует ли значение у, при котором 9у-7 и 9у+5 равны?

Творческий вопрос. Как вы думаете, чем уравнение |𝑥|=1 отличается от уравнения x=1?

Вопрос интерпретация. Почему x=5 не может быть корнем уравнения ?

Практический вопрос. На каких уроках, кроме алгебры, вам приходится решать уравнения?

Прием позволяет развить у учащихся мыслительные навыки, необходимые не только в учёбе, но и в обычной жизни. Умение принимать взвешенные решения, работать с информацией, анализировать различные стороны явлений и так далее. Данная технология направлена на развитие ученика, основными показателями которого являются оценочность, открытость новым идеям, собственное мнение и рефлексия собственных суждений.

Включение в урок дидактических игр и игровых моментов активизирует творческую деятельность школьников. Более результативным является применение дидактических игр на уроках закрепления, систематизации и обобщения знаний, чем на уроках открытия нового знания. На каком этапе урока следует применять дидактическую игру, определяет учитель. И это зависит от дидактической задачи урока.

Игра может быть обучающей, контролирующей, обобщающей. Если учащиеся в процессе игры или при подготовке к ней получают новые знания, умения или навыки, то это обучающая игра. Мотив познавательной деятельности здесь заключается не только в игре, но и в содержании изучаемого математического материала. Если дидактическая цель игры заключается в повторении и проверке полученных школьниками знаний, умений и компетенций, то это контролирующая игра. В математике часто применяются обобщающие игры, основанные на интеграции знаний и межпредметных связей.

Дидактические игры на уроках математики следует организовывать в соответствии с дидактическими задачами урока. Дидактическая цель ставится в виде игровой задачи. Учебная деятельность учащихся на уроке подчиняется правилам игры. Учебный математический материал, с которым работает школьник на уроке, является средством игры.  В учебную деятельность вводятся элементы соревнования и это переводит дидактическую задачу в игровую. Игровой результат должен быть связан с правильностью выполнения дидактической задачи.

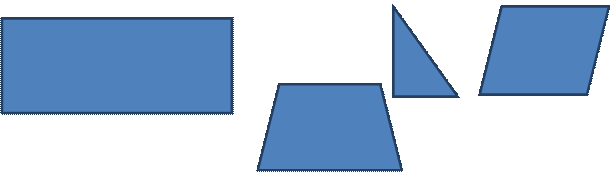
Приведем пример обобщающей игры «Столяры» по теме «Площади» (8 класс). Перед началом игры учитель может познакомить школьников с многообразием строительных профессий с помощью виртуальной экскурсии и рассказать о профессии столяра. Возможно, в качестве предварительной подготовки, дать задание школьникам посмотреть, что такое паркет и какие бывают виды паркетных покрытий. Затем классу выдается задача: Детский сад «Солнышко» заказал выполнение работ по настилу паркета в игровой комнате длиной 5,75 метров и шириной 8 метров. Но при этом пожелание заказчика такое, что число треугольных плиток должно быть минимальным, а количество стальных плиток одинаковое. Размер и форма паркетных плиток, предоставляемых магазином, указаны на рисунке 1:

Рис.1 Размер и форма паркетных плиток

Рассчитать количество паркетных плиток, необходимых для выполнения работ и изготовить модель паркетного пола в масштабе 1:10 для согласования с заказчиком. Далее, на усмотрение учителя для конкретного класса, возможны дополнительные условия и задания. Например, рассчитать смету работ, если дана стоимость и количественный состав упаковок плитки, реализуемых магазином и стоимость определенного вида работ столяров. Затем обсуждаются правила игры, возможно деление на бригады, возможно ограничение по времени.

Творческие задания– вид учебной деятельности школьников, в которой они целенаправленно усваивают знания, приобретают умения и навыки, которые используются потом в создании нового, посредством комбинации прошлого опыта. Применение творческих заданий на уроках математики формирует у школьников не только интерес к предмету, но и убежденность в том, что они создают что-то новое. На уроках математики можно использовать следующие творческие задания и задачи:

- составление школьниками по изученному материалу практико-ориентированных задач, связанных с действительностью. Направленность задач может быть любая, в зависимости от конкретного населенного пункта или времени года. Например, задачи на нахождение геометрических фигур в архитектурных сооружениях города Борисоглебска;

- составление задач, в том числе обратных данным, задач по графикам и диаграммам;

- сочинение сказок, рассказов, составление кроссвордов по изученным темам;

- исследовательские задания;

- конструирование и моделирование;

- творческие домашние задания, например, математические сочинения. Темы сочинений могут быть такими: «История квадратных уравнений»; «Треугольники вокруг нас»;

- задачи с лишними или недостающими данными. Например, задача с недостающими данными пи изучении темы «Четырехугольники» в 8 классе. «Периметр прямоугольника 8 см, а сумма двух его сторон 6 см. Найдите длины сторон прямоугольника»;

- задачи с неопределенными данными;

- задачи, решаемые различными способами;

- логические задачи;

- нестандартные задачи, занимательные задачи, старинные задачи. Примером может служить нестандартная задача для 5-6 классов. «Девять осликов за 3 дня съедают 27 мешков корма. Сколько корма надо пяти осликам на 5 дней?».(Ответ. 25 мешков. Находим сколько мешков съедают 9 осликов в один день 27:3=9. Затем находим, сколько мешков съедает один ослик в один день 9:9=1 мешок. Пять осликов в один день съедают 5 мешков, следовательно,  5 осликов за 5 дней съедают 25 мешков)

Еще один пример. В 3 часа дня настенные часы отбивают три удара за 12 секунд. Согласны ли вы с утверждением, что в 6 часов вечера эти часы отобьют 6 ударов за 24 секунды. Ответ обоснуйте. (Ответ. Нет. Промежутков между тремя ударами всего 2, каждый из которых длится 12:2=6 (с). Если часы отбивают 6 ударов, то промежутков между ударами будет 5. Значит, 6 ударов будут отбиты на этих часах за 30 сек.)

Список используемой литературы

1.    Данчук И.И., Данчук М.П.Организация творческой деятельности школьников в технологическом образовании как социально значимая психолого-педагогическая проблема//Известия Южного федерального университета. Педагогические науки Издательство: Южный федеральный университет (Ростов-на-Дону), №8, 2016. С 45-56

2.    Дорофеев Г.В, Петерсон Л.Г. Математика. 6 класс. Часть 2 – Изд. 2-е, перераб. / Г.В. Дорофеев, Л.Г Петерсон. – М.: Издательство «Ювента», 2018. – 112 с.

3.                      Дорофеев Г.В, Петерсон Л.Г. Математика. 5 класс. Часть 2 – Изд. 2-е, перераб. / Г.В. Дорофеев, Л.Г Петерсон. – М.: Издательство «Ювента», 2018. – 176 с.

4.    Забелина С. Б.Опроблеме готовности к творческой деятельности участников образовательного процесса. // Забелина С. Б., Казаков Н. А., Пинчук И.  А. Вестник Московского государственного областного университета. Серия: Педагогика №2,2020 с.47-56

5.    Малькова, Е. Ю. Об использовании сведений из истории математики на уроках / Е. Ю. Малькова, И. Б. Фомичёва. — Текст:// Молодой ученый. — 2015. — № 20 (100). — С. 477-480. — URL: https://moluch.ru/archive/100/22662/ (дата обращения: 03.02.2021).

6.    Манвелов С. «Основы творческой разработки уроков», ПС «Математика»,1997 г. № 11, 13, 19, 21.

7.    Математика: 5 кл. учеб. / Н. Я. Виленкин, В. И. Жохов, А.С. Чесноков, С. И. Шварцбурд.— 34-е изд., стереотип. — Москва: Мнемозина, 2016 . - 280 с. : ил.

8.    Математика: 6 кл. учеб. / Н. Я. Виленкин, В. И. Жохов, А.С.Чесноков, С. И. Шварцбурд.— 34-е изд., стереотип. — Москва: Мнемозина, 2016

9.    Национальная образовательная инициатива «Наша новая школа». URL: http://минобрнауки. рф/documents/1450.

Скачано с www.znanio.ru