
1. Приклади розв’язання типових задач контрольної роботи
Задача 1
Для споживача із функцією корисності товарів
![]()
знайти функцію попиту на обидва
товари за цінами ![]() та доходом Q.
та доходом Q.
1. Визначити вектор, який
дорівнює значенню попиту на товари за конкретними цінами ![]() та доходом Q = 24.
та доходом Q = 24.
2. Знайти на скільки процентів зміниться попит на перший товар при збільшенні ціни на другий товар на 1% з компенсацією доходу. Відповідь дати у загальному вигляді та знайти число для визначеного вектору попиту. Використати рівняння Слуцького.
Приклад розв’язання задачі.
2.
1. Знайдемо точку попиту споживача із
функцією корисності ![]() . Маємо
. Маємо
3.
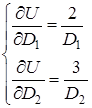 .
.
4. Далі виконаємо такі дії
5.
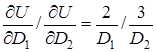 ,
,
6. звідси
7.
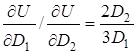 .
.
8. Відомо, що залежність між похідними функції корисності та цінами на основі використання 2-го закону Госсена така:
9.
![]() .
.
10. Одержимо
11.
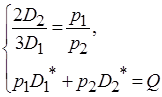 .
.
12. Розв’яжемо цю систему
13.
 .
.
14. А тому
15.
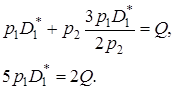
16. Звідси
17.
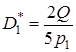 ,
,
18.
 .
.
19. Підставляємо значення
20.
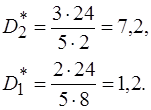
21.
22. 2. Для подальшого розв’язання використаємо рівняння Слуцького
23.
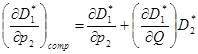 .
.
24. Із попереднього рішення відомо, що
25.
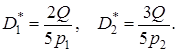
26. Тоді
27.
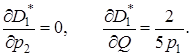
28. А тому
29.
 .
.
30. Для пошуку еластичності попиту на перший товар при зміні ціни на другий товар з компенсацією доходу треба знайти
 (%).
(%).
Задача 2
Визначити залежність попиту D(p)=10 - p та пропозиції S(p)=-5+2p від ціни p.
1. Взначити рівнозважену ціну p*.
2. Розглянути умови, при яких стан рівноваги для функцій попиту та пропозиції в павутиноподібній моделі стійкий.
3. Використовуючи умови п.2, прослідкувати декілька ітерацій наближення до стану рівноваги для функцій попиту та пропозиції. Використати аналітичний та графічний способи.
4. Доказати аналітичним та графічним способами, що стан рівноваги для функцій попиту та пропозиції нестійкий за умови невиконання п.2.
5. Знайти доход при рівнозваженій ціні та побудувати графік доходу від ціни.
Приклад розв’язання задачі.
1. Для визначення рівнозваженої ціни p* розглядається рівняння
D(p*)= S(p*),
10-p*=-5+2p*,
p*=5.
2. Далі знаходимо похідні функцій попиту та пропозиції
D’(p)=-1, S’(p)=2.
Для того щоб визначити як буде змінюватися ціна, необхідно порівняти похідні
S’(p) > |D’(p)|,
2 > |-1|.
Виходячи з цього порівняння, ціна буде змінюватися від найменшої до найбільшої. Це і буде умовою стійкості системи.
3. Для графічного рішення задачі спочатку будуємо графіки функцій попиту та пропозиції. Для цього виконуємо такі дії:
D(p)=0, p=10,
p=0, D(p)=10,
S(p)=0, p=2.5,
p=0, S(p)=-5.
Охарактеризувати стан рівноваги аналітичним способом зручно за допомогою таблиці 6.1.
Таблиця 6.1.
|
p |
2.5 |
6.25 |
4.37 |
… |
|
D(p) |
7.5 |
3.75 |
5.63 |
… |
|
S(p) |
0 |
7.5 |
3.75 |
… |
Результати розрахунків з таблиці наносимо на графік функцій попиту та пропозиції (рисунок 6.1).

Рисунок 6.1
4. Для того щоб довести, що стан рівноваги у системі нестійкий, необхідно порушити умови стійкості та змінювати ціну від найбільшої до найменшої (рисунок 6.2).
Аналітичний спосіб рішення задачі наведено в таблиці 6.2.
Таблиця 6.2
|
p |
10 |
-5 |
… |
|
D(p) |
0 |
15 |
… |
|
S(p) |
15 |
-15 |
… |
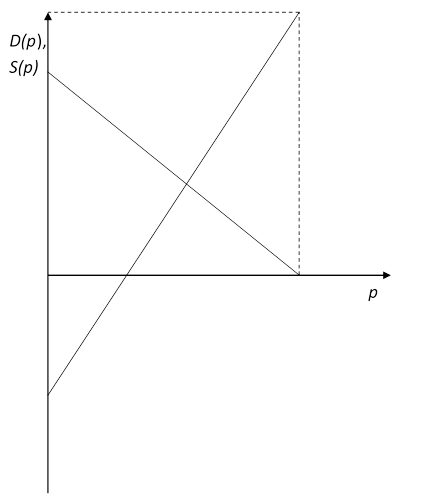
Рисунок 6.2
5. Доход функцій попиту та пропозиції знаходиться за формулами:
QD(p)=p*Q(p)=10p-p2,
QS(p)=p*S(p)=-5p+2p2.
Таким чином доход при рівнозваженій ціні буде дорівнювати:
QD(p)=10*5-25=25 (ум.од.),
QS(p)=(-5)*5+2*25=25 (ум.од.).
Для побудови графіку доходу використаємо допоміжну таблицю 6.3.
Таблиця 6.3
|
p |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
QD(p) |
0 |
9 |
16 |
21 |
24 |
25 |
24 |
|
QS(p) |
0 |
-3 |
-2 |
3 |
12 |
25 |
42 |
Графіки доходу показані на рисунку 6.3.
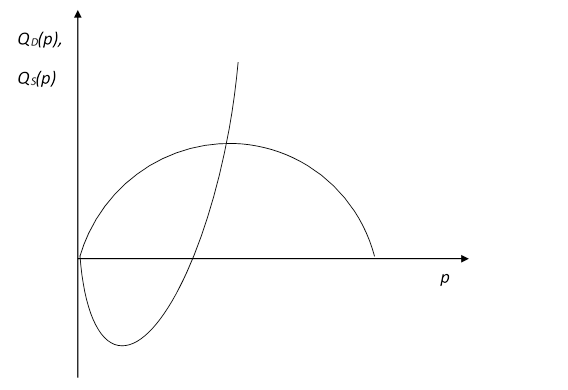
Рисунок 6.3
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.