МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН

ТАШКЕНТСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ НИЗАМИ

Кафедра «Общей  математики»

КУРСОВАЯ РАБОТА

по курсу: «Математического анализа»

на тему: «Приложение принципа сжимающих отображений в анализе – теории пределов»

Работу выполнил: студент  группы МПМ 302Р

физико-математического факультета

направления образования «5110100- Методика преподавания математики»

Чепухалин С. А.

Проверил: доцент  кафедры «Общей  математики»

Тургунбаев Р. М.

Ташкент - 2019 год

Оглавление

Вступление. 3

1.      Метрические пространства. 5

Полные метрические пространства. 5

2.      Принцип сжимающих отображений. 11

Применение принципа сжимающих отображений к нахождению пределов. 11

3.      Применение принципа сжимающих отображений к интегральным уравнениям.. 15

4.      Применение принципа сжимающих отображений к дифференциальным уравнениям.. 20

5.      Разработка практических рекомендаций для повышения эффективности обучения принципу сжимающих отображений и его применения в анализе студентов высших учебных заведений. 23

Заключение. 24

Список используемой литературы. 25

Вступление.

Актуальность. Принцип сжимающих отображений – один из базовых методов функционального анализа. В данной курсовой работе изложены возможности применения принципа сжимающих отображений – для исследования вопросов существования и единственности решений наиболее распространенных типов диф. и интегральных уравнений. В описанном подходе органично сочетаются как идейная простота, так и универсальность применения к самым различным по постановке математическим проблемам, а также глубина получаемых результатов. Дополнительным достоинством еще является и то, что одновременно с доказательством существования решений предлагается эффективный алгоритм для его поиска.

Объект исследования – сжимающие отображения.

Предмет исследования – применение принципа сжимающих отображений в анализе.

Цель: Провести анализ применения принципа сжимающих отображений при решении задач математического анализа и других  областей математики.

Задачи: 1. Изучить принцип сжимающих отображений.

2. Провести анализ применения принципа сжимающих отображений в различных областях математики.

3. Показать актуальность его применения при решении задач математического анализа.

4. Провести разработку практических рекомендаций для повышения эффективности обучения принципу сжимающих отображений и его применения в анализе студентов высших учебных заведений.

Содержание. В первом разделе дано определение метрического и полного метрического пространства, приведены примеры на доказательства, являются ли заданные функции метрическим пространством, является ли пространство полным, а также задания операторов в полных метрических пространствах.

Во втором разделе описан принцип сжимающих отображений, доказана теорема Банаха о неподвижной точке, приведены примеры на определение, являются ли данные отображения сжимающими, доказательство и нахождения пределов последовательности, нахождение решений системы уравнений методом последовательных приближений с заданной точностью.

В третьем разделе рассказывается о применении принципа сжимающих отображений к линейным и нелинейным интегральным уравнениям.

Четвертый раздел повествует о применении принципа сжимающих отображений к дифференциальным уравнениям.

1.                     Метрические пространства.

Полные метрические пространства.

 Расстояние было одно из первых понятий, которые человек стал использовать для изучения и описаний окружающего мира. Со временем это составило основу науки названой «геометрия». Там были сформулированы ряды аксиом, которые должно удовлетворять расстоянию. При развитии математики эти понятия утратили свой первоначальный смысл, и стало использоваться как меры различия объектов произвольной природы. Такая трактовка расстояния с обобщением других понятий позволила выявить обобщенность методов в разных разделах математики, и разработать универсальные подходы к решению совершенно не связанных между собой задач. Такое направление математической теории стало называться «функциональным анализом». Мы используем результаты функционального анализа при исследовании вопросов существования и единственности решений диф. и интегральных уравнений. Во многих учебниках по функциональному анализу определение метрического пространства (МП) дается так:

«Множество М называется метрическим пространством, если каждой паре его элементов х, у поставлено в соответствие неотрицательное число ,  удовлетворяющее следующим условиям:

1)  тогда и только тогда, когда х = у (аксиома тождества);

2)  (аксиома симметрии);

3)для любых х, у, z из М (аксиома треугольника).

Число  называется расстоянием между элементами х и у, а перечисленные условия — аксиомами метрики. Элементы метрического пространства называются точками. Функцию  называют также метрикой на М.»

1.1. Пусть M — любое множество. Положим

Докажите, что  — метрика на М.

Решение: Пусть х, у, z ϵ М и  проверим, выполняются ли аксиомы метрики:

1.   Когда х = у  ⇔   (по условию);

2.   Если

3.   При

; (I)

При

; (II)

         Ответ: есть метрика на М.

1.2. Являются ли метриками на прямой следующие функции: 

а) ;

б) ;

в) ;

г) ;

д) ?

Решение: а)  ˄  х, у, z ϵ R:

х = у  ⇔  ,

;

;

;

Ответ: есть метрика на R.

б)  ˄  х, у, z ϵ R:

х = у  ⇔  ,

 аксиома тождества не выполняется.

Ответ: не является метрикой на R.

в)  ˄  х, у, z ϵ R:

х = у  ⇔  ,

;

;

;

Ответ: есть метрика на R.

г)  ˄  х, у, z ϵ R:

х = у  ⇔  ,

;

 аксиома симметрии не выполняется.

Ответ: не является метрикой на R.

д)  ˄  х, у, z ϵ R:

х = у  ⇔  ,

;

 аксиома симметрии не выполняется.

Ответ: не является метрикой на R.

Пусть М — метрическое пространство с метрикой ρ. Открытым (замкнутым) шаром в М радиуса  с центром в точке  называется множество всех точек х ϵ М, для которых  .  Сферой радиуса r > 0 с центром в точке  называется множество всех точек

х ϵ М, таких, что.

Последовательность  точек метрического пространства М называется фундаментальной, если для любого δ > 0 можно указать такой номер N, что для всех n и m, больших N, выполняется неравенство .

Метрическое пространство, в котором всякая фундаментальная последовательность сходится, называется полным. Полное нормированное линейное пространство называется банаховым пространством.

1.3. Докажите, что всякое компактное метрическое пространство М полно.

Доказательство: Пусть  — фундаментальная последовательность из М. Т. к. М компактно, то из этой последовательности можно извлечь сходящуюся под последовательность .

Пусть Покажем, что и . Пусть δ — произвольное положительное число. Т. к. последовательность  фундаментальна, то найдется такое N, что  при n > N и m > N. А Т. к. , то найдется такое k, что  и . Тогда при n > N имеем:

и . Значит, действительно .

Мы доказали, что любая фундаментальная последовательность из М сходится, а это и означает, что М полно.

1.4. Является ли полным пространство М натуральных чисел с метрикой:

Решение: Пусть — последовательность (натуральных чисел) точек этого пространства. Если все члены ее, начиная с некоторого номера, совпадают ( при k > K), то

и эта последовательность является фундаментальной. А т. к.  при k > K, то  при k > K, и это означает, что .

Если же в последовательности  при любом сколь угодно большом К имеются члены , то в силу того, что

, такая последовательность не является фундаментальной.

Итак, фундаментальными в данном пространстве могут быть лишь последовательности, постоянные с некоторого номера, и они сходятся. Это — полное пространство.

Пусть М — метрическое пространство. Всякое полное метрическое пространство , в котором имеется часть , плотная в  и изометричная М, называется, пополнением пространства М. Справедлива теорема Хаусдорфа о том, что у всякого метрического пространства М существует и с точностью до изометрии единственное пополнение .

Так способ определения метрики во многом зависит от требования решаемой задачи, из их анализа часто становится ясно, какие элементы следует считать близкими.

Примером в качестве меры отличия непрерывных функций на отрезке [a, b] x(t) и y(t) можно принять величину

.                                (1)

Убедится, что множество непрерывных функций с такой метрикой является МП. Выполнение первых 2-х аксиом очевидно. Докажем же аксиому треугольника. Для  t ∈[a, b] имеем

|x(t)-z(t)|=|[x(t)-y(t)]+[y(t)-z(t)]| ≤ max _a≤t≤b |x(t)-y(t)|+max _a≤t≤b |x(t)-y(t)=ρ(x, y)+ρ(y, z)

Т. к. полученное неравенство справедливо при всех , то и

.

Т. о., множество непрерывных функций на отрезке [a, b] с метрикой (1) является МП и обозначается символом C[a, b].

При решении многих физ. задач оказалось необходимо требование интегрируемости квадрата данных функций, т.е. условие

,                                                          (2)

которое значит конечность энергии данного физ. процесса. В таком случае расстояние между функциями определяется как

ρ (x, y)=() ^½.                            (3)

Покажем же, что множество, составленное из этих функций, является МП. Наиболее сложной оказалась проверка аксиомы треугольника, которая опирается на использование неравенства Коши–Буняковского

() ² ≤  ⋅.           (4)

В справедливости его можно убедиться таким образом.

Для  действительного параметра значение интеграла

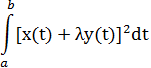
 неотрицательно, что соответствует неравенству

 2λλ²  ≥ 0

 Обозначим входящие в него интегралы через γ,β,α, получим  αλ²+2βλ+γ ≥ 0.

Поскольку при  значениях параметра этот квадратный 3-хчлен является неотрицательным, то его дискриминант 4β²−4γα ≤ 0, с учетом введенных обозначений из него следует неравенство, (4).

 Обращаясь к доказательству аксиомы треугольника

 . (5)

Для удобства введем обозначения:

 x(t)− y(t)=u(t), y(t)− z(t)=v(t).

Тогда неравенство, (5) записываем в виде

. (6)

Произведя оценку интеграла, входящего в левую часть неравенства, с используя неравенство Коши-Буняковского, (4)

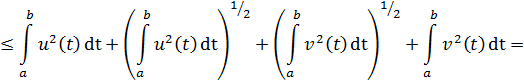
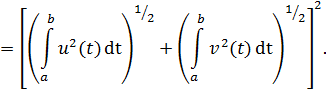
После извлечения корня из обеих частей и возврата к исходным функциям, мы приходим к неравенству, (5).

Т. о., доказали, что множество квадратично интегрируемых функций на отрезке [a, b] с метрикой, (3) является МП. Для его обозначения используют символ L₂[a, b].

Определение полного метрического пространства обычно дается следующим образом.

«Метрическое пространство М называется полным, если любая последовательность {x_n} элементов этого пространства, для которой ρ(x_n, x_m)→ 0 при , сходится к некоторому элементу пространства М.»

Рассмотренные МП C[a, b] и L₂ [a, b], являются полными. Доказательство этого можно найти во многих курсах функционального анализа.

Дадим определение заданного оператора. «Если каждому элементу x метрического пространства X по некоторому закону поставлен в соответствие определенный элемент y метрического пространства Y , то говорят, что в X задан оператор A со значениями в пространстве Y и пишут .»

 И приведем примеры заданий операторов.

 Если функции x(t), ϵ , поставлена в соответствии функция , где

K(t, s) – непрерывная функция из аргументов  , то мы определим тем оператор  , который получит название «интегрального оператора Фредгольма». Далее покажем, что функция  ϵ C[a, b].

 Через C^∞(a, b) обозначим пространство функций , определенных, бесконечно дифференцируемых на (a, b). Каждой функции поставим в соответствие производную . Тем мы введем диф. оператор , действующий из C^∞(a, b) в C^∞(a, b). 

2.                     Принцип сжимающих отображений.

Применение принципа сжимающих отображений к нахождению пределов.

 Одним из эффективных приемов для доказательства теорем существования и единственности решений диф., интегральных и всех функциональных уравнений является принцип сжимающих отображений. Широко применяется этот принцип и связано это с тем, что он определяет условия однозначного разрешения уравнения, и дает его приближенные решения.

Пусть — отображение метрического пространства М в себя. Точка х ϵ М, для которой , называется неподвижной точкой отображения .

Отображение  метрического пространства М в себя называется сжимающим, если существует такое число α (0 < а < 1), что для любых x₁, х₂ ϵ М выполняется неравенство

2.1. Является ли сжимающим отображение  промежутка [3, ∞) в себя?

Решение:

Ответ: Отображение  промежутка [3, ∞) в себя является сжимающим.

2.2. Является ли отображение  числовой прямой в себя сжимающим?

Решение:

⇒ Отображение  промежутка (-∞, +∞) в себя не является сжимающим.

2.3. Покажите, что функция  отображает отрезок [9, 10] в себя. Сжимающее ли это отображение?

Решение: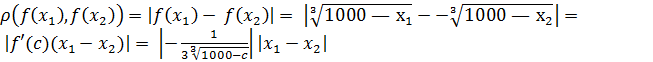

Ответ: Отображение  промежутка [9, 10] в себя является сжимающим.

Пусть  — отображение метрического пространства М в себя. Последовательность точек этого пространства , (n ϵ N; х_о — произвольная точка М) называется последовательностью последовательных приближений (или итераций) для отображения .

2.4. Докажите, что следующие последовательности имеют пределы, и найдите их:

а)

б) … .

Решение: а)  Данная последовательность, очевидно, удовлетворяет такому рекуррентному соотношению:  

т. е. она представляет собой последовательность итераций для функции  

Функция f отображает в себя полное метрическое пространство . Это сжимающее отображение:

Тогда по теореме Банаха отображение f имеет на  единственную неподвижную точку, и к ней сходятся последовательные приближения f при любом выборе начального приближения .

Это означает, что и рассматриваемая последовательность имеет предел, причем он равен неподвижной точке отображения f. Найдем эту точку:

б) Данная последовательность, очевидно, удовлетворяет такому рекуррентному соотношению:  

т. е. она представляет собой последовательность итераций для функции  

Функция f отображает в себя полное метрическое пространство . Это сжимающее отображение:

Тогда по теореме Банаха отображение f имеет на  единственную неподвижную точку, и к ней сходятся последовательные приближения f при любом выборе начального приближения .

Это означает, что и рассматриваемая последовательность имеет предел, причем он равен неподвижной точке отображения f. Найдем эту точку:

2.5. Покажите, что система

имеет единственное решение, и найдите его с точностью до 0,01 методом последовательных приближений, выбрав за начальное приближение точку, (0,0,0).

Решение: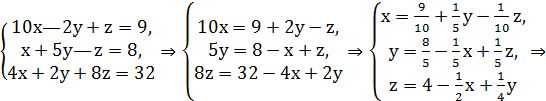

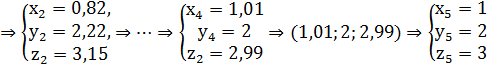
Ответ:(1;2;3)

Рассмотрим следующую теорему.

«Пусть в полном метрическом пространстве задан оператор A, отображающий элементы пространства X в элементы этого же пространства, и для всех x, y ∈ X

 .                              (7)

Тогда существует единственный элемент x₀ , такой, что

Ax₀=x₀.»

 Оператор, который обладает свойством, (7) называется сжимающим, а x₀ – неподвижной точкой оператора A .

 Возьмем для доказательства произвольный элемент x из X и построим следующую последовательность  x₁=Ax , x₂=Ax₁ , ..., x_n=Ax_n-1 , ...

Расстояние между элементами данной последовательности определяется соотношением

 ρ(x₁, x₂)=ρ(Ax, Ax₁) ≤ αρ(x, x₁)=αρ(x, Ax),

ρ(x₂, x₃)=ρ (Ax₁, Ax₂) ≤ αρ(x₁, x₂) ≤ α2ρ(x, Ax),

...

ρ(x_n, x _n-1) ≤ αⁿρ(x, Ax),

...

 С этим учетом

.                 (8)

А также в силу условия  

и потому  при  и .

 Т. к. пространство X по условиям полное, то  элемент пространства, который является пределом данной последовательности,

 .

Убедиться, что x₀ неподвижная точка оператора A, можно, осуществить предельный переход  в равенстве

 Докажем единственность неподвижной точки. Пусть существует 2 такие точки – x₀ и y₀ , то есть A x₀=x₀ и A y₀=y₀ .

Тогда

.

Допустим, что  , то из соотношения выше получим α ≥1, это противоречит условию, (7). Значит, оператор A имеет одну единственную неподвижную точку x₀ .

 В силу теоремы построения последовательных приближений , которые сходятся к неподвижной точке  , можно начинать с любого элемента x из X. Выбор этого элемента, конечно, будет влиять и на скорость сходимости. Оценить n-ое приближение и скорость сходимости получится, переходя к пределу  по формуле, (8):

 Чтобы применить данный принцип к уравнению конкретного вида, надо представить это уравнение в форме  и выбрать подходящее полное МП, где действует оператор A , затем убедиться, что сжимающимся является этот оператор. 

3.                     Применение принципа сжимающих отображений к интегральным уравнениям

3.1. Линейные уравнения

 Рассмотрим неоднородное линейное интегральное уравнение Фредгольма 2-го рода

.                                (9)

Используем оператор

,                                  (10)

И перепишем уравнение, (9) в виде

.                                           (11)

Доказательство существования решений уравнения, (9) сходится к вопросу наличия у оператора A неподвижной точки , то есть функции, которая переводится оператором саму в себя.

 Сначала предположим, что ядро уравнения непрерывное в своем основном квадрате  и, ограничено: . Искать решение уравнения, (9) будем в пространстве , считать, что  принадлежит также этому пространству.

 При применении принципа сжимающих отображений необходимо, показать, что оператор A при задаваемых условиях отображает в себя полное пространство . Используем неравенство Коши-Буняковского, (4) и проверяемое неравенство  , получим

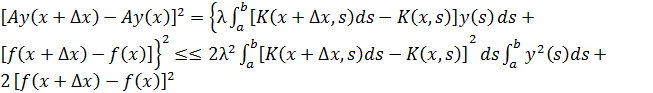                                                                                                (12)

Правая часть неравенства, (12) при  стремится к нулю, что свидетельствует об непрерывности функции  , то есть ее принадлежности ко пространству .

 Выясним, при каких условиях оператор A будет сжимающим. Имея

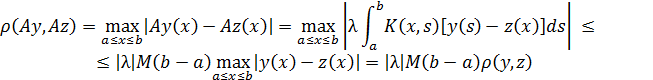
Заключаем по принципу сжимающих отображений, что при

                               (13)

оператор A –  сжимающийся, а уравнение, (9) с непрерывным свободным членом и ядром имеет одно единственное непрерывное решение. Последовательные приближения  к данному решению из соотношений могут быть найдены

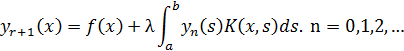
при выборе  в качестве любой непрерывной функции на .

 Ограничение, (13) может быть, ослабим, если отказаться от требований непрерывности свободного члена и ядра уравнения, (9).

Предположим, что , а  удовлетворяют условию

                             (14)

Решение уравнения, (9), принадлежащее также пространству . В этом случае оператор, (10) отображает известное полное пространство в само себя. Исходя из неравенства, (6), имеем

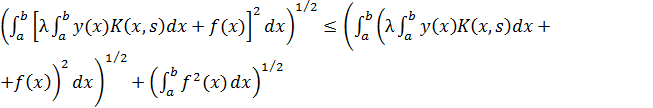                     (15)

Воспользуемся неравенством Коши-Буняковского, (4) получим

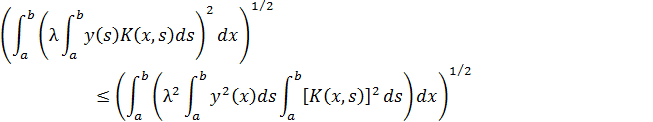
Т. о., правая часть неравенства, (15) при высказанных выше условиях является ограниченной, значит, оператор A переводит в себя пространство .

 Определим ограничения, которые выполняют условие, (7) принципа сжимающих отображений. Используем неравенство Коши-Буняковского, (4) получаем

 Интегрируем обе части неравенства по x от a до b , и найдем

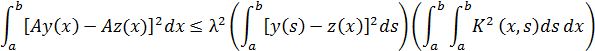
или

.

Видим, условие, (7) выполняется при

                       (16)

Т. о., опираемся на принцип сжимающих отображений, приходим к выводу, интегральное уравнение, (9) имеет одно единственное решение.

 Можно также показать, что , при этом равенство возможно только при .  Это условие, (16) полагает менее жесткое ограничение, на λ, чем условие, (13). Что является следствием, что класс функций, принадлежащих к пространству , шире, чем пространства . Дальнейшее ослабевание требований к функциям, входящих в уравнение, (9), приведем к расширению диапазона доступных значений для λ, при коих решение и будет существовать. Верхняя граница λ определяет величину минимума собственного значения.

В случае, когда свободный член в уравнении, (9) , изложенные выше рассуждения остаются. Это значит, что интегральное однородное уравнение Фредгольма 2-го рода при условиях, (13) или, (16) имеет одно единственное решение. Путем подстановки можно убедиться, этим решением является функция , то есть тривиальное решение. Единственность же будет гарантирована только при выполнении всех условий. А при их нарушении возможно также существование и других решений.

 3.2. Нелинейные уравнения

 Принцип сжимающих отображений применяется также к решению некоторых других видов нелинейных интегральных уравнений.

 Необходимо решить уравнение

                              (17)

При непрерывности функций  и  по всем аргументам оператор

                                (18)

будет отображать в себя полное пространство . Потребуем, чтобы подынтегральная функция (17) удовлетворяла условиям Липшица по u , то есть

|,                     (19)

где L – постоянная.

Найдем условия, когда оператор, (18) будет сжимающим. Для любых 2-х функций  и  ϵ , имеем

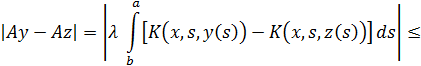
Такая оценка справедлива при , и, значит

.

Т. о., при  оператор A будет сжимающим, а уравнение, (17) будет одно единственное непрерывное решение. Решение может быть найдено при использовании итераций

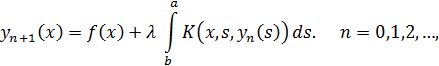
в качестве начального приближения берем произвольную непрерывную функцию.

В качестве 2-го примера возьмем интегральное уравнение Вольтера

.                 (20)

Это уравнение можно рассматривать как отдельный случай уравнения, (17), то при тех условиях на функции  и  где оператор, (18) отображает в себя полное пространство .

Заметим, значение искомой функции в любой точке x определяется значением этой функции на отрезке , в отличии от уравнения, (17), где функция в каждой точке зависит от ее значений на всем отрезке. Что позволяет использовать также уже вычисленные значения , а для нахождения ее значений в более удаленных от начала точках.

 Берем отрезок  т. о., чтобы его длина  удовлетворяла условиям , при котором оператор, (18) будет сжимающим. Значит, на этом отрезке  одно единственное решение уравнения, (20). Рассмотрим также отрезок , где  . И запишем уравнение, (20)

.

В силу, что на отрезке  функция  определена однозначно, 2-ой интеграл можно считать функцией известной и добавить к . Для полученного уравнения на  выполняется также условие сжимаемости оператора, (18), и решения уравнения, (20) будет единственным. Повторим рассуждения для последующих отрезков такой же длины, мы придем к выводу, что существует решение и оно единственно на всем отрезке .

 В частном случае, где уравнение, (20) линейно, то есть  всегда выполняется условие Липшица, (19), т. к. непрерывная функция  ограничена, а в качестве L выбирается . Из этого факта выходит, что линейное уравнение Вольтера для непрерывных правой части и ядро всегда имеет одно единственное решение. 

4.                     Применение принципа сжимающих отображений к дифференциальным уравнениям

  Рассматривая дифференциальное уравнение 1-го порядка

                 (21)

с заданным изначальным условием  . Пусть  – непрерывная функция по всей совокупности аргументов на прямоугольнике  ,  , и ограниченная в нем, то есть  . Кроме того,  удовлетворяет условию Липшица

 .                  (22)

 Исследуя вопрос об существовании и единственности решений уравнения, (21) в пространстве непрерывных функций , определенных на отрезке меньшем , таких, что  . Значение δ будет определено из нашего дальнейшего рассмотрения.

 Воспользуемся равнозначностью уравнения, (21) и интегрального уравнения

.                                 (23)

 Выясняя, при каких условиях интегральный оператор

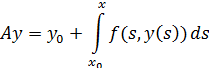
отображает в себя пространство . Если непрерывные функции , и , то результат действия оператора будет также непрерывной функцией, тогда имеет место

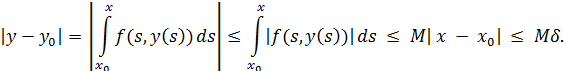
Для непрерывности  необходимо,  , из этого следует, что параметр δ должен удовлетворять , точнее . При выполнении условия оператор A переводит в себя пространство .

 Остается убедиться, что этот оператор является сжимающим при условии достойной малости.

Выбирая 2 произвольные непрерывные функции  и  мы примем во внимание, (22) что имеем

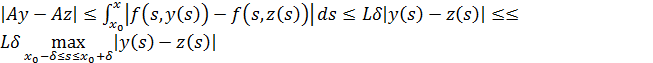
В силу справедливости этой оценивания для  из заданного интервала

Т. о., при условии  интегральное уравнение, (23) и, следовательно, диф. уравнение, (21) будут иметь одно единственное непрерывное решение.

 Мы доказывали существование, и единственность решений в окрестности начала точки x₀. Выбрав в этой окрестности новую точку и повторяя рассуждения, можно продолжить решение по такой окрестности, в которой остаются выполненными требуемые нам условия. С помощью похожей процедуры можно доказывать существование и единственность решений в более обширной области.

 Для существования решений, но не для единственности достаточно только непрерывности правой части уравнения, (21). Тщательный анализ показывает, решение может быть единственным и при менее жёстких условиях на .

 Теперь обратимся к частному случаю уравнения, (21), где

, где  и  – непрерывные функции.

Это уравнение называется линейным. На отрезке непрерывности, непрерывности функций p(x) и q(x) будут ограниченными, то есть, в частности, . В таком случае условие, (22) выполнится автоматически при . Т. о., для линейного случая решение уравнения, (21) единственно существует в области непрерывности функций p(x) и q(x). Такое же утверждение справедливо и для интегрального уравнения Вольтера 2-го рода, при  существует одно единственное решение, если непрерывные входящие в уравнение функции.

 Принцип сжимающих отображений может использоваться и при исследовании систем диф. и интегральных уравнений. С учетом равносильности системы диф. уравнений и уравнений n-го порядка легко устанавливают условие разрешимости последнего.

В этом разделе мы воспользовались одним из более простых методов из функционального анализа и для исследования фундаментальных вопросов в теории диф. и интегральных уравнений. Сфера же применений функционального анализа очень многообразна. Особо эффективны его методы при решении нелинейных уравнений, наиболее интересны с точки зрения физ. приложений. Положительность использования методов этого раздела в современной математики во многом обусловлена, что сформулированные обобщения в его рамках позволяют выявиться и сосредоточить на самых ключевых вопросах задачи, не обращая особо внимания на несущественные детали.

5.     Разработка практических рекомендаций для повышения эффективности обучения принципу сжимающих отображений и его применения в анализе студентов высших учебных заведений.

Принцип сжимающих отображений хотя и является одним их применяемых методов в математическом анализе и других областях математики, он по какой-то причине трудно дается в понимании студентам, а, следовательно, и его применение. Т. к. объектом моего исследования являются сжимающие отображения, я решил разработать несколько практических рекомендаций для повышения эффективности обучения принципу сжимающих отображений и его применения.

Одним из первых методов наилучшего понимания материала дать студентам самостоятельно изучить поставленный вопрос, а потом проверить степень его понимания, а в следствии корректировать, дополнять и расширять усвоенные знания. Я пришел к этому выводу когда готовился по курсовой работе, т. к. я начал работать над ней еще до того как сжимающие отображения мы проходили на лекционных занятиях.

Вторым критерием, безусловно, является наглядность, если студент на визуальном уровне поймет, в чем заключается данный принцип, увидит область его применения, он лучше запомнит и в дальнейшем при аналогичных ситуациях будет его применять. Наиболее наглядными примерами являются отображение участка числовой прямой в себя ,  и т. п. Наиболее наглядными примерами применения принципа сжимающих отображений, на мой взгляд, являются нахождение пределов последовательности и решение системы линейных уравнений методом итераций.

Заключение.

Мы рассмотрели один из базовых методов функционального анализа - принцип сжимающих отображений. Данный принцип нашел широкое применение в различных областях не только математики, но и физики, химии, биологии, экономики и других науках.

В математическом анализе применение принципа сжимающих отображений в основном используются для исследования вопросов существования и единственности решений наиболее распространенных типов диф. и интегральных уравнений.

Как мы можем сделать вывод, что принцип сжимающих отображений стал своеобразным «вынужденным», предопределенным этапом в развитии функционального анализа и математической науки в целом. Его применение решило много задач, как в фундаментальных исследованиях, так и прикладного характера.

Список используемой литературы.

1.                     Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: Наука. Гл. ред. физ.-мат. лит., 1976.

2.                     Петров В. А., Виленкин Н. Я., Граев М. И. Элементы функционального анализа в задачах. – М.: Просвещение, 1978.

3.                     Люстерник Л. А., Соболев В. И. Элементы функционального анализа. – М.: Наука. Гл. ред. физ.-мат. лит.,1965.

4.                     Канторович Л. В., Акилов Г. П. Функциональный анализ – М.: Наука. Гл. ред. физ.-мат. лит., 1984.

5.                     Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. – М.: Мир, 1983.

6.                     Антоневич А.Б., Радыно Я.В. Функциональный анализ и интегральные уравнения – Минск: Университетское, 1984.

7.                     Краснов М.Л. Интегральные уравнения. Введение в теорию. – М.: Наука. Гл. ред. физ.-мат. лит., 1975.

8.                     Мышкис А.Д. Математика для технических вузов: специальные курсы. – СПб.: Изд-во "Лань", 2002.

9.                     Шилов Г.Е. Математический анализ. Функции одного переменного. Ч. 3. – М.: Наука. Гл. ред. физ.-мат. лит., 1970.

10.                 Скачано с www.znanio.ru