Приложение2_математика 9 класс_арифмет и геом прогрессии

1. Три числа , ,  в указанном порядке образуют геометрическую прогрессию. Найдите х.

Ответ:   6.

2. В геометрической прогрессии  сумма третьего, шестого и девятого членов равна 5, а сумма девятого, двенадцатого и пятнадцатого членов равна 40.       Найдите: .

Ответ:

3. В арифметической прогрессии сумма третьего, седьмого, четырнадцатого и восемнадцатого членов равна 52. Найти сумму двадцати первых членов прогрессии.

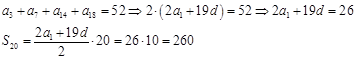
Ответ:  260.

4. В арифметической прогрессии сумма пятого, восьмого, семнадцатого и двадцатого членов равна 48. Найти сумму двадцати четырех первых членов прогрессии.

, 

Ответ:  288.

5. Три числа составляют геометрическую прогрессию. Если от третьего числа отнять 4, то числа составляют арифметическую прогрессию. Если же второй и третий члены полученной арифметической прогрессии уменьшить на 1, то снова получится геометрическая прогрессия. Найти три исходных числа.

Пусть   a, b, c – геометрическая прогрессия, а  a, b, c – 4 – арифметическая прогрессия, тогда a, b –1, c – 5  – новая геометрическая прогрессия. Следовательно,

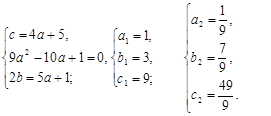
 Ответ: 1) 1; 3; 9;     2)  

6. Три числа образуют геометрическую прогрессию. Если второе число увеличить на 2, то прогрессия станет арифметической, а если после этого увеличить последнее число на 9, то прогрессия снова станет геометрической. Найти три исходных числа.

Пусть   a, b, c – геометрическая прогрессия, а  a, b + 2, c – арифметическая прогрессия, тогда a, b + 2, c + 9  – новая геометрическая прогрессия. Следовательно,

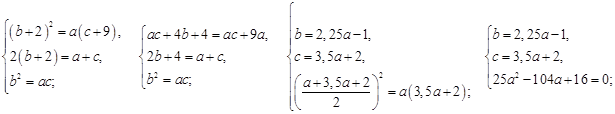
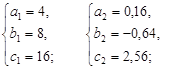
Ответ:   1) 4; 8; 16;                  2) 0,16; –0,64; 2,56.