Приложение_5 (домашняя работа)

Приложение 5

Домашнее задание можно  предложить учащимся решить наиболее эффективным способом, который выбирает ученик.

Задание №1

Три числа составляют геометрическую прогрессию. Если из третьего числа вычесть 4, то числа составят арифметическую прогрессию. Если же из второго и третьего членов полученной арифметической прогрессии вычесть по единице, то снова получим геометрическую прогрессию. Найти эти числа.

Решение:

Разумеется, эту задачу можно решить любым из способов, разобранных в примере 1, например последним. Так как три числа образуют геометрическую прогрессию, то их можно записать в виде а; aq; aq². После вычитания из последнего числа 4 получаем числа a; aq; (aq² - 4), образующие арифметическую прогрессию. На основании свойства арифметической прогрессии имеем:

 2aq = a + (aq² -4), или 4 = а(1 - q)².

Если из второго и третьего членов этой арифметической прогрессии вычесть по единице, то получим числа a; (aq - 1); (aq² - 5), образующие геометрическую прогрессию.

Запишем ее свойство: (aq - 1)2 = a(aq² - 5), или 1 = a(2q - 5).

Для определения a и q имеем систему уравнений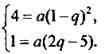 

Разделив уравнения друг на друга, получим:  или q2 – 10q + 21 = 0. Корни этого уравнения q = 3 и q = 7, тогда соответствующие значения: a = 1 и a = 1/9. Теперь находим сами числа: 1; 3; 9 и 1/9; 7/9; 49/9.

Задание №2

Три числа, сумма которых 93, составляют геометрическую прогрессию. Эти числа можно также рассматривать как первый, второй и седьмой члены арифметической прогрессии. Найти данные три числа.

Решение:

Так как числа образуют геометрическую прогрессию, то их можно записать в виде b; bq; bq². Их сумма равна 93, имеем первое уравнение: b + bq + bq² = 93.

Первые два числа образуют арифметическую прогрессию, и ее разность d = bq - b. Тогда легко записать седьмой член арифметической прогрессии: b + 6(bq - b) = 6bq - 5b. По условию задачи этот член равен третьему члену геометрической прогрессии bq2. Получаем второе уравнение: 6bq - 5b = bq², или 0 = q2 - 6q + 5, откуда q = 1 и q = 5.

Тогда из первого уравнения находим b: 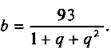 При q = 1 b = 31 и данные числа: 31, 31; 31; при q = 5  и числа: 3, 15; 75. Итак, данные числа: 31, 31; 31 и 3, 15; 75.