
«Применение подобия треугольников
к решению практических задач»
Конспект урока по предмету «геометрия»
8 класс
2018 г.
Аннотация.
Урок геометрии в 8 классе по теме «Применение подобия треугольников к решению практических задач».
|
Название технологии для организации урока с позиции системно-деятельностного подхода |
Используемые |
|
|
Методы |
Приемы |
|
|
Технология проблемного обучения |
-проблемно-поисковый; - метод коллективного решения проблем; - самостоятельная работа.
|
- Проблемные вопросы; - Тестовая проверка знаний.
|
Тема урока: «Применение подобия треугольников к решению практических задач»
Цель урока: показать практическую направленность темы: «Подобие треугольников».
Задачи урокаповторить признаки подобия треугольников, рассмотреть их применение к решению задач; развивать умение работать в парах; воспитывать бережное отношение к своему здоровью и здоровью окружающих.
ü обучающие:научить обучающихся взаимосвязи теории с практикой; познакомить учащихся с различными способами определения высоты предмета; формировать умения применять полученные знания при решении разнообразных практическихзадач.
ü развивающие:активизация познавательной деятельности учащихся; формирование качества мышления, характерные для математической деятельности и необходимые для продуктивной жизни в обществе.
ü воспитывающие:мотивирование интереса учащихся к предмету посредством включения их в решение практических задач.
Личностные УД:
- умение работать в парах, слушать собеседника и вести диалог, аргументировать свою точку зрения.
Познавательные УД:
- ориентироваться в своей системе знаний;
- проводить анализ учебного материала;
- извлекать информацию, представленную в разной форме;
- формулировать конечный результат действий.
Регулятивные УД:
- самостоятельно формулировать тему урока;
- определять и формулировать цель деятельности на уроке;
- развитие навыков и способностей критического мышления.
Коммуникативные УД:
- слушать и понимать речь других;
- уметь с достаточной полнотой и точностью выражать свои мысли;
- договариваться и приходить к общему решению в совместной деятельности;
- использовать знаково-символические записи математического понятия.
Тип урока: изучение нового материала
Используемые технологии: проблемное обучение, развивающее обучение.
Форма организации деятельности учащихся: фронтальная, индивидуальная, парная.
Оборудование: проектор, ноутбук, доска, раздаточный материал, презентация.
Список используемых источников:
1. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Поздняк, И.И. Юдина Геометрия 7-9 классы: учеб. Для общеобразоват. Организаций. – М.: Просвещение, 2016.
2. https://oge.sdamgia.ru
План урока
1. Организационный момент.
2. Актуализация усвоенных УУД знаний учащихся.
3. Формулировка темы и целей урока.
4. Применение теоретических основ при решении практических задач.
5. Закрепление материала.
6. Самостоятельная работа по определению уровня усвоения знаний, умений и навыков.
7. Применение теоретических основ при построении треугольника Серпинского для расширения кругозора обучающихся.
8. Подведение итогов. Рефлексия.
Ход урока:
|
Деятельность учителя |
Деятельность учеников |
||||
|
1. Организационный момент. Приветствие учителя и учащихся, определение отсутствующих. Проверка подготовленности учащихся к уроку. - Сегодня на уроке мы работаем не в тетрадях, а на рабочих листах, которые вы мне сдадите в конце урока. Подпишите на них Ф.И.(Приложение 1)
2. Актуализация усвоенных УУД знаний учащихся. - Посмотрите, пожалуйста, на экран.(Приложение 2, Слайд 1) Что вы видите? (пирамиды) А еще? (треугольники) Какие? (подобные) - А с помощью чего можно доказать, что эти треугольники подобные? (с помощью признаков подобия треугольников) - Сформулируйте 1 признак подобия треугольников. - Сформулируйте 2 признак подобия треугольников. - Сформулируйте 3 признак подобия треугольников.
- Ребята, а где, кроме уроков геометрии можно применить признаки подобия треугольников? (в жизни)
3. Формулировка темы и целей урока. - Сформулируйте тему урока. Запишите в рабочих листах «Практическое применение признаков подобия треугольников». (Слайд 2)
4. Применение теоретических основ при решении практических задач. И сегодня я предлагаювооружившись знаниями геометрии выяснить практическую значимость знаний, которые приобретаются в процессе учёбы в школе.
Рассмотрим старинную задачу.(Слайд 3) Способ 1 «Способ Фалеса Милетского» Задача 1. Греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Фалес избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна так же равняться длине отбрасываемой ею тени. Длину тени надо было считать от средней точки квадратного основания пирамиды; ширину этого основания Фалес мог измерить.
- Каковы преимущества это способа? (не требует вычислений) - Каковы недостатки? (можно определить высоту предмета только в короткий промежуток времени, в солнечную погоду и когда нет рядом предметов, тени которых сливаются с тенью данного предмета)
- А где в нашей жизни можем применить этот способ? (для вычисления высоты дерева, здания…)
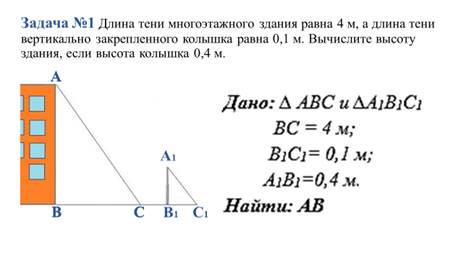
5. Закрепление материала. - Давайте решим задачи.(Слайд 4, 5) №1 Длина тени многоэтажного здания равна 4 м, а длина тени вертикально закрепленного колышка равна 0,1 м. Вычислите высоту здания, если высота колышка 0,4 м.
x:4=0,4:0,1 x=4*0,4:0,1 x=16 Ответ: Высота многоэтажно здания 16 метров.
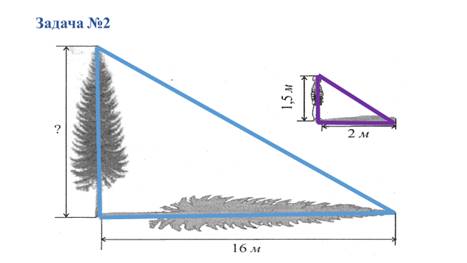
№2 Сформулируйте условие задачи и решите ее в парах.(Слайд 6)
- В жизни много встречается задач, которые можно решить с помощью признаков подобия треугольников. Следующую задачу я взяла из сборника заданий ОГЭ математика 9 класс.
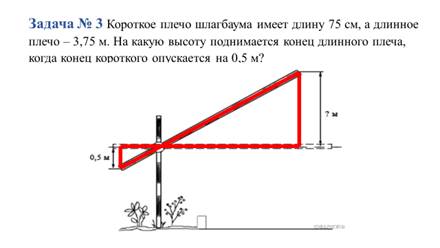
№ 3. Короткое плечо шлагбаума имеет длину 75 см, а длинное плечо – 3,75 м. На какую высоту поднимается конец длинного плеча, когда конец короткого опускается на 0,5 м?(Слайд 7)
x:0,5=375:0,75 x=2,5 Ответ: на 2,5 метра поднимается конец длинного плеча.
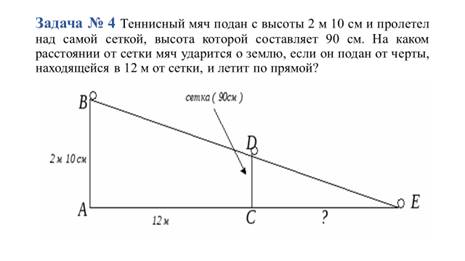
№ 5. Теннисный мяч подан с высоты 2 м 10 см и пролетел над самой сеткой, высота которой составляет 90 см. На каком расстоянии от сетки мяч ударится о землю, если он подан от черты, находящейся в 12 м от сетки, и летит по прямой?(Слайд 8)
210:(12+х)=90:х 210х=90(12+х) 210х=1080+90х 120х=1080 х=9 Ответ: На расстоянии 9 метром от сетки мяч ударится о землю. 6. Самостоятельная работа. (Приложение 3)(Слайд 9) Если у вас все верно, то поставьте в рабочих листах «5», если есть ошибки, то «!». 7. Применение теоретических основ при построении треугольника Серпинского.(Слайд 10) А теперь выполним задание в рабочих листах – треугольник Серпинского. Для этого разделите равносторонний треугольник со стороной а на 4 равных треугольника. Центральный раскрасьте в красный цвет. Затем 3 треугольника еще раз разделите на 4 равных треугольника. Каждый центральный раскрасьте в синий цвет. Найдите по вариантам коэффициенты подобия треугольников (1 вариант самый большой к красному, 2 вариант красный треугольник к синему).
Рассмотрите треугольники:
Итак, какие вы получили значения для коэффициента подобия? (К=2). Итак, мы получили очень интересную фигуру, которая называется самоподобной. Фигуры, каждый элемент которой подобен себе, французский математик Мандельброт назвал фракталами. Существуют фракталы, созданные ученными и созданные природой.(Слайд 11) (Фрактал (лат. fractus — дробленый, сломанный, разбитый) — термин, означающий сложную геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком) Какие они, фракталы? (Слайд 12-15)
8.Итоги урока: а теперь скажите мне, каков багаж знаний вы приобрели на сегодняшнем уроке, что нового узнали? (признаки подобия треугольников широко применяются в жизни – в быту, в спорте, в архитектуре, в строительстве…) Да, действительно, зная законы геометрии, мы многое открыли для себя. А какой признак подобия чаще использовался для доказательства подобия треугольников? (первый) Домашнее задание: 3. Творческое задание: Найти способ нахождения высоты, используя зеркало. 4. Карточка с задачами из ОГЭ. Если урок понравился и все понятно, то поставьте в рабочих листах «+», если что-то осталось не понятным, то «!». Рефлексия.Сейчас я вас попрошу выйти к доске, сдать листы и поместить магнитик в треугольник, если урок вам понравился, тема понятна, работать было комфортно. Иначе, магнит поместите вне треугольника! И в заключении мне хотелось бы сказать: Геометрия – это наука, которая обладает всеми свойствами хрустального стекла, такая же прозрачная в рассуждениях, безупречная в доказательствах, ясная в ответах, гармонично сочетающая в себе прозрачность мысли и красоту человеческого разума. Геометрия до конца не изученная наука, и может быть, многие открытия ждут именно вас. Желаю удачи в дальнейшем изучении науки. |
Готовность к уроку
Фронтальная работа с классом
Кластер Кластер Кластер
Фронтально
Объяснение учителя у доски
Фронтальная беседа
Оформление дано, найти на листах. Комментирование с мест. Решение оформляется на доске
Работа на местах в парах
Работа на листах, краткое оформление решения.
Работа в парах
Работа на доске, краткое оформление решения.
Индивидуальная работа на карточках
Фронтальная работа на листах
Индивидуальная работа на листах
найти определение в Интернете (1 ученик)
Ответы детей
Записано в электронных дневниках
|
Приложение 1
ФИ____________________________
Тема:
|
Задания |
Оцени себя |
||
|
Задача 1.Длина тени многоэтажного здания равна 4 м, а длина тени вертикально закрепленного колышка равна 0,1 м. Вычислите высоту здания, если высота колышка 0,4 м.
BC = B1C1=
Найти: AB B C B1 C1
Решение: ∆ ~ ∆ Пусть х= , тогда: ----- = ----- = ----- ; ----- = -----
х= -----------------
х= Ответ: |
|
||
|
Задача 2. Решение:
Пусть х= , тогда:
----- = ----- = ----- ; ----- = -----
х= -----------------
х= Ответ:
|
|
||
|
Задача 3. Короткое плечо шлагбаума имеет длину 75 см, а длинное плечо – 3,75 м. На какую высоту поднимается конец длинного плеча, когда конец короткого опускается на 0,5 м?
∆ ~ ∆ Пусть х= , тогда:
----- = ----- = ----- ; ----- = -----
х= -----------------
х=
Ответ: |
|
||
|
Задания |
Оцени себя |
||
|
Задача 4. Теннисный мяч подан с высоты 2 м 10 см и пролетел над самой сеткой, высота которой составляет 90 см. На каком расстоянии от сетки мяч ударится о землю, если он подан от черты, находящейся в 12 м от сетки, и летит по прямой?
Решение:
∆ ~ ∆
Пусть х= , тогда: ----- = ----- = ----- ; ----- = -----
х= -----------------
х= Ответ: |
|
||
|
САМОСТОЯТЕЛЬНАЯ РАБОТА
|
|
||
Вычисления:
|
|
||
|
ИТОГ УРОКА |
|
Приложение 2
Слайд 1

Слайд 2

Слайд 3

Слайд 4
Слайд 5

Слайд 6
Слайд 7
Слайд 8
Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Приложение 3
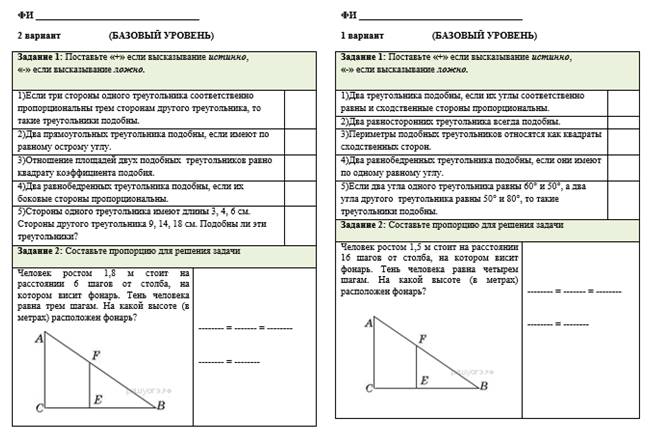

Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.