МБОУ Коелгтнская СОШ

 им. Дважды Героя Советского Союза С.В.Хохрякова

Интегрированный урок по теме:

«Применение производной к исследованию функций. Схема исследования функции».

практическое применение знаний и умений с использованием компьютерных технологий

Алгебра + информатика

Учитель математики 

Рыбак Марина Александровна

Учитель информатики 

Лазарева Наталья Николаевна

с. Коелга.

«Применение производной к исследованию функций. Схема исследования функции».

практическое применение знаний и умений

Цель:

1. Сформировать навыки исследования функции с помощью производной по заданному алгоритму и уметь вносить данные в программу EXCEL для  постороения графика.
2. Развивать алгоритмическое мышление, память.
3. Воспитывать графическую культуру, культуру устной и письменной речи.

План занятия:

1. Организационный момент ;
2. Актуализация опорных знаний ;
3. Объяснение нового материала ;
4. Закрепление
5. Итог занятия ;
6. Домашнее задание

Оборудование

• мультимедиа презентация
• раздаточный материал
• мультимедиа проектор.

Ход занятия

1. Орг. момент.

Сегодня нам предстоит научиться проводить полное исследование функции и строить ее график.   Мы  с вами впервые попробуем элемент урока алгебры перенести на урок информатики и посмотреть свои результаты на машинах.

2. Актуализация опорных знаний.

Устная работа по графику выявить точки максимума и минимума, промежутки возрастания и убывания и т.д.

3. Закрепление изученного материала.

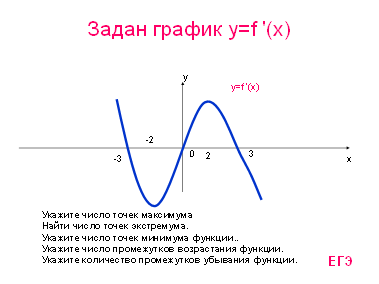
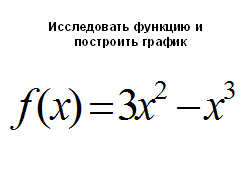
Пусть дана функция: . Решение: 1.      D(f)=R, т.к. f -многочлен. 2.      Выясняем, является ли функция f четной или нечетной.  - функция ни четная, ни нечетная. 3.      Функция непериодическая. 4.      Находим точки пересечения графика с осями координат: 5.      а) с осью ОХ: у=0 получаем точки (0;0), (3;0) 6.      б) с осью ОУ: х=0 получаем точки (0;0) 7.      Найдем производную функции: 8.      Найдем критические точки: , т.е. 6х-3х2=0, х=0 или х=2. Отмечаем эти точки 0 и 2 на числовой прямой, и определяем знак производной в каждом промежутке.     I. (-1)   6(-1)-3(-1)2=-6-3=-9<0 II. (1)  6*1-3*12=3>0 III. (3) 6*3-3*32=-9<0 Значит, в промежутках  и  функция убывает и (0;2) – функция возрастает.    х=0 - точка минимума, т.к. производная меняет знак с минуса на плюс. Вычислим уmin=0. х=2 – точка максимума, т.к. производная меняет знак с плюса на минус. Вычислим уmax=4. 9.Составляем таблицу для внесения всех данных x 0 (0;2) 2 - 0 + 2 - f(x) 0 4     min   max     10. Строим график функции.

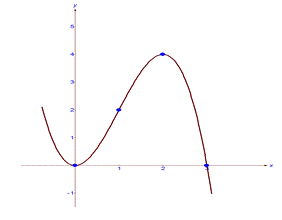
4.  Домашнее задание. Проблема- задача.

Внимание!!!

Рекомендую прежде чем начать работу ответить на вопросы стратегии, ответы будут являться планом. 

У кого возникнут проблемы  с задачей предлагаю другую работу.

Выучить схему исследования функции.

Исследовать и построить график функции:

а) y = 3x⁴- 4x³ - 12x² + 10;

5. Самостоятельная работа.

По одному человеку садятся за компьютеры, остальные работают в тетрадях. После окончания решения проверяют электронный вариант и бумажный, ставят самооценку.

Вариант I.

Пример 1. Исследуйте функцию f(x)= x³-3х² и постройте ее график

Решение:

Область определения данной функции - множество действительных чисел: D (f) =R.

Данная функция непрерывна на множестве действительных чисел как многочлен.

Найдем критические точки функции: f '(x)=3х²-6х = 3х (х-2),

f '(x)=0, 3х (х-2)=0, х=0 или х=2.

Составляем таблицу

Критические точки разбивают координатную прямую на три промежутка: (-; 0), (0; 2), (2; ).

Рис.5 (знаки f ')

На рисунке 5 указаны знаки производной f '(x) на каждом из этих промежутков.

Найдем нули функции: x³-3х² = 0, x² (х-3) = 0, x = 0 или x = 3.

Найдем координаты еще одной точки графика: если x =-1, то f (-1) = (-1)³ - 3 * (-1)² = -4.

6) Строим график данной функции

Пример 2. Сколько корней имеет уравнение: x⁴ - 4x³ - 9 = 0.

Решение:

р (x) = x⁴ - 4x³ - 9

D(р) = (-; ).

р ' (x) = 4 x ³- 12x ² = 4 x ² (х-3) = 0, x_1,2 = 0; x₃ = 3

Рис.6 (знаки р ').

4) Из рисунка 6 видно, что: р(x) убывает на интервале (- ; 3];

р (x) возрастает на [3; +).

5) x = 3 - min

а) р _min= р (3) = 3⁴ - 4 * 3³ - 9 = -36 < 0

б) в точке x = 0 график имеет точки перегиба (то есть меняет выпуклость), f (0) = -9.

6) Строим эскиз графика

График пересекает ось 0Х в двух точках x₁ и x₂, следовательно, многочлен, а значит и данное уравнение имеет два корня.

Вариант II.

Пример 1. Исследуйте функцию y = 1/3x³- 3x² + 8x и постройте ее график.

Решение:

Область определения данной функции - множество действительных чисел: D (y) =R.

Данная функция непрерывна на множестве действительных чисел .

Найдем критические точки функции: y ' = x² - 6x + 8.

y ' = 0, x² - 6x + 8 = 0, x = 2 или x = 4.

4) Составляем таблицу

y_max = y(2) = 20/3, y _min= y(4) = 16/3.

5) Найдем нули функции: 1/3x³- 3x² + 8x =0, x (1/3x²- 3x + 8) = 0, x = 0 или 1/3x²- 3x + 8 = 0.

x²- 9x + 24 = 0, D = 9²- 4 * 24 < 0, квадратное уравнение корней не имеет. Данная функция имеет только один нуль: x = 0. При x = 0 y = 0 - график функции проходит через начало координат.

6) Построим график функции

Пример 2. Сколько корней имеет уравнение: x²- x³/3- 1= 0

Решение:

p (x) = -x³/3+ x²- 1.

D (p) = IR.

Исследуем функцию: p '(x) = -x²+ 2x = - x (x - 2) =0, x = 0 или x =2.

3) Найдем критические точки функции

Рис.7 (знаки p')

x = 0 - min, p _min= p (0) = -1 < 0;

x = 2 - max, p _max= p (2) = - 8/3 + 4 - 1 = -8/3 +3 = 1/3 > 0.

4) Строим эскиз графика.

График пересекает ось 0Х в трех точках x₁, x₂ и x₃, следовательно, многочлен, а значит и данное уравнение имеет три корня.

6. Рефлексия. Спасибо, ребята. До свидания.